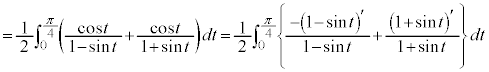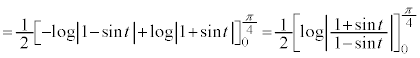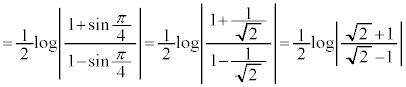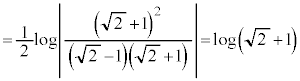東大理系数学'22年前期[1]
次の関数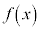 を考える。
を考える。
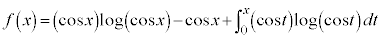 (
(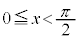 )
)(1) 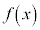 は区間
は区間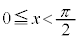 において最小値を持つことを示せ。
において最小値を持つことを示せ。 (2) 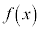 の区間
の区間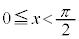 における最小値を求めよ。
における最小値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 積分方程式の問題ですが、積分方程式を解かなくても解答できてしまいます。
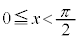 より
より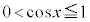 ,
,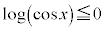
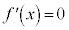 とすると、
とすると、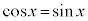 または
または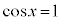
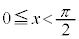 においては、
においては、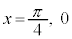
増減表は、以下のようになります(関数の増減を参照)。 増減表より、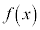 は区間
は区間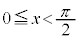 において最小値を持ちます。
において最小値を持ちます。
(2) (1)の増減表より、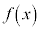 が区間
が区間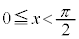 においてとる最小値は
においてとる最小値は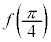 です。
です。 与式の積分を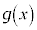 とおいて、
とおいて、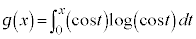 とすると、
とすると、 よって、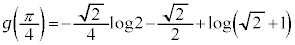
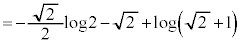 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。