���嗝�n���w'22�N�O��[5]
���W��ԓ��̓_A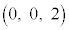 �Ɠ_B
�Ɠ_B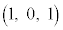 �����Ԑ�����z���̂܂���1��]�����ē�����Ȗʂ�S�Ƃ���BS��̓_P��xy���ʏ�̓_Q��
�����Ԑ�����z���̂܂���1��]�����ē�����Ȗʂ�S�Ƃ���BS��̓_P��xy���ʏ�̓_Q��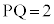 �����Ȃ��瓮���Ƃ��A����PQ�̒��_���ʉ߂�����͈͂�K�Ƃ���BK�̑̐ς����߂�B
�����Ȃ��瓮���Ƃ��A����PQ�̒��_���ʉ߂�����͈͂�K�Ƃ���BK�̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ȉ��̉́A�����O����킩���Ă���A�����ƈႤ���̂ɂȂ�Ǝv���܂��B�����ł́A�������ōl����i�߂�悤�ȗ���ʼn��܂��B
�Ȗ�S�͒��~���ł��Bzx���ʏ�Œ���AB��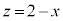 �ƕ\����܂��B�Ȗ�S��̓_P��z���W��t (
�ƕ\����܂��B�Ȗ�S��̓_P��z���W��t (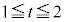 )�Ƃ���ƁA�_P��zx���ʏ�ɗ���Ƃ��A�_P��x���W�́A
)�Ƃ���ƁA�_P��zx���ʏ�ɗ���Ƃ��A�_P��x���W�́A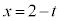 �ƂȂ�A�Ȗ�S���A�_P���܂�z���ɐ����ȕ���
�ƂȂ�A�Ȗ�S���A�_P���܂�z���ɐ����ȕ���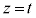 �Ő����Ƃ��ɂł������̉~��
�Ő����Ƃ��ɂł������̉~��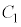 ��̓_��z���Ƃ̋�����
��̓_��z���Ƃ̋�����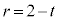 �ł��B
�ł��B
 �E�}���A�O�p�`�̑�������A1�F
�E�}���A�O�p�`�̑�������A1�F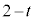 = 1�Fr�Ƃ��āA
= 1�Fr�Ƃ��āA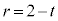 �Ƌ��߂邱�Ƃ��ł��܂��B
�Ƌ��߂邱�Ƃ��ł��܂��B
�_P�́Az����̓_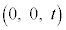 �𒆐S�Ƃ��锼�ar�̉~��
�𒆐S�Ƃ��锼�ar�̉~��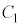 ��̓_�Ȃ̂ŁA����
��̓_�Ȃ̂ŁA����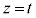 ��ŁA���̍��W�͎���θ��p���āA
��ŁA���̍��W�͎���θ��p���āA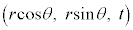 �ƕ\���܂�(�~�̔}��ϐ��\�����Q��)�B
�ƕ\���܂�(�~�̔}��ϐ��\�����Q��)�B
�_P����xy���ʂɐ���PH�����낷�ƁA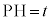 ���A
���A
�_P���狗��2�ł���_�́A�_P�𒆐S�Ƃ��锼�a2�̋��ʏ�̓_�ł����A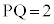 �ł���xy���ʏ�_Q�́A���̋��ʂ�xy���ʂŐ����Ƃ��ɂł������̉~��
�ł���xy���ʏ�_Q�́A���̋��ʂ�xy���ʂŐ����Ƃ��ɂł������̉~��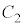 ��̓_�ł��B���̉~��
��̓_�ł��B���̉~��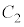 �̒��S�͓_H
�̒��S�͓_H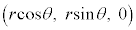 �C���a��QH�ł��B�_Q�̍��W�͎���φ��p���āA
�C���a��QH�ł��B�_Q�̍��W�͎���φ��p���āA
�ƕ\����܂��B����PQ�̒��_M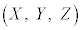 �̍��W�́A
�̍��W�́A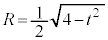 �Ƃ��āA
�Ƃ��āA
θ�Cφ���S�������Ƃ��ē����Ƃ��̓_M�̒ʉߔ͈͂�K�Ȃ̂ł����A2�̕ϐ�θ�Cφ�������̂ł́A�l���ɂ����̂ł��B���̂܂܋��s������@���ʉ��Ō�q���܂����A�����ł͐}�`�I�ɍl�@���܂��B
��L������ƁA�_M�́A����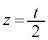 ��ŁA�_
��ŁA�_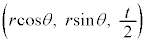 �𒆐S�Ƃ��锼�aR�̉~��
�𒆐S�Ƃ��锼�aR�̉~��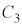 ��̓_�ɂȂ��Ă��܂��B�~��
��̓_�ɂȂ��Ă��܂��B�~��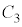 �̒��S��z����̓_
�̒��S��z����̓_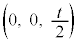 �𒆐S�Ƃ��锼�ar�̉~��
�𒆐S�Ƃ��锼�ar�̉~��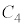 ��ɂ���܂��B�܂�Aθ�Cφ���S�������Ƃ��ē����Ƃ��A�~��
��ɂ���܂��B�܂�Aθ�Cφ���S�������Ƃ��ē����Ƃ��A�~��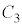 �́A���̒��S��
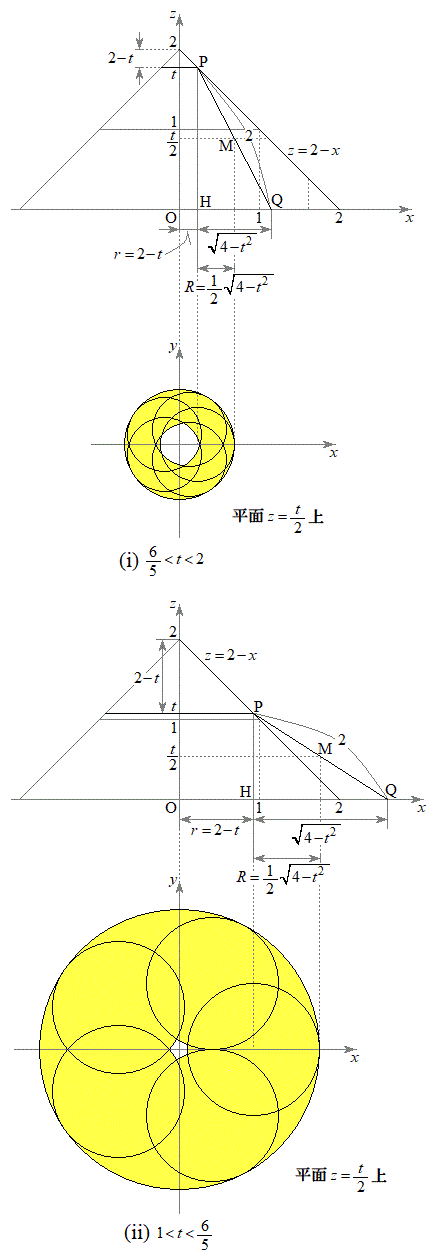
�́A���̒��S��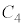 ����Ȃ��瓮�����ƂɂȂ�܂��B���̒ʉߔ͈͉͂E�}�̉��F���F���̂悤�ɂȂ�܂�(����
����Ȃ��瓮�����ƂɂȂ�܂��B���̒ʉߔ͈͉͂E�}�̉��F���F���̂悤�ɂȂ�܂�(����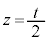 ��Ȃ̂ŁA�}��x���Ay���́A���ꂼ��A���ۂ�x���Ay�������̕��ʏ�܂�xy���ʂƐ����ȕ����ɕ��s�ړ����������̂ɂȂ�܂�)�B�����ɁA�_M���ʉ߂��Ȃ��������ł��邱�Ƃɒ��ӂ��Ă��������B
��Ȃ̂ŁA�}��x���Ay���́A���ꂼ��A���ۂ�x���Ay�������̕��ʏ�܂�xy���ʂƐ����ȕ����ɕ��s�ړ����������̂ɂȂ�܂�)�B�����ɁA�_M���ʉ߂��Ȃ��������ł��邱�Ƃɒ��ӂ��Ă��������B
�ʉߔ͈͂̊O���̉~���́Az����̓_�𒆐S�Ƃ��锼�a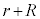 �̉~���ł��B
�̉~���ł��B
�����ŁA���ƂȂ邱�Ƃ�����܂��B�ʉߔ͈͂̓����̉~�����l�������̂ł����AR��r�̑召�W��������܂���B
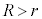 �Ƃ���ƁA
�Ƃ���ƁA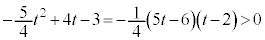 ���A
���A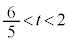
���̂Ƃ��A�E�}(i)�̂悤�ɁAz���ɋ߂��Ƃ���ɁA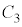 ���ʉ߂��Ȃ��������ł��܂��B���̕����́A
���ʉ߂��Ȃ��������ł��܂��B���̕����́A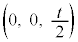 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a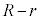 �̉~�ɂȂ�܂��B
�̉~�ɂȂ�܂��B
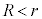 �̂Ƃ��A�܂�A
�̂Ƃ��A�܂�A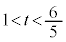 �̂Ƃ��ɂ́A�E�}(ii)�̂悤�ɁA��͂�z���ɋ߂��Ƃ���ɁA
�̂Ƃ��ɂ́A�E�}(ii)�̂悤�ɁA��͂�z���ɋ߂��Ƃ���ɁA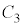 ���ʉ߂��Ȃ��������ł���̂ł����A���̕����́A
���ʉ߂��Ȃ��������ł���̂ł����A���̕����́A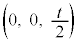 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a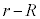 �̉~�ɂȂ�܂��B
�̉~�ɂȂ�܂��B
�ǂ���̏ꍇ������K��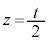 �Ő����Ƃ��̒f�ʂ̖ʐς́A
�Ő����Ƃ��̒f�ʂ̖ʐς́A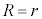 �̏ꍇ���܂߂āA
�̏ꍇ���܂߂āA
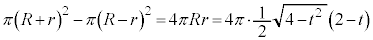 (
(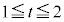 )�@����@
)�@����@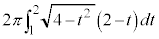 �ł͂���܂���Bt �́A�_P��z���W�ł����āA�_M��z���W�ł͂Ȃ�����ł��B�_M��ʂ镽�ʂŐ����f�ʐς��@�Ȃ̂ŁA�ϕ��͓_M��z���W�ɂ��čs���K�v������܂��B
�ł͂���܂���Bt �́A�_P��z���W�ł����āA�_M��z���W�ł͂Ȃ�����ł��B�_M��ʂ镽�ʂŐ����f�ʐς��@�Ȃ̂ŁA�ϕ��͓_M��z���W�ɂ��čs���K�v������܂��B
�f�ʐχ@��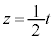 (
(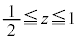 )�ŕ\���ƁA�@�́A
)�ŕ\���ƁA�@�́A
�ƂȂ�܂��B�����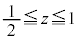 �͈̔͂Őϕ����āA���߂�K���̐�V�́A
�͈̔͂Őϕ����āA���߂�K���̐�V�́A
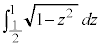 �́A���a1�̉~��
�́A���a1�̉~��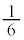 ����A���
����A���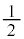 �C����
�C����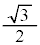 �̎O�p�`������������(�u���ϕ�(����2)���Q��)�ŁA
�̎O�p�`������������(�u���ϕ�(����2)���Q��)�ŁA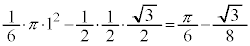
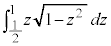 �́A
�́A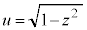 �Ƃ���(�u���ϕ����Q��)�ƁA
�Ƃ���(�u���ϕ����Q��)�ƁA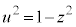 �Cz�F
�Cz�F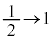 �̂Ƃ��Au�F
�̂Ƃ��Au�F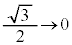 �C
�C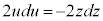 ���A
���A
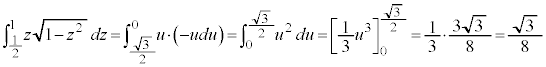 ��
�� 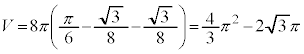 ......[��]
......[��]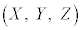 �̍��W�ɂ��āA
�̍��W�ɂ��āA
�̂܂܁A�v�Z�����Ői�߂�Ƃǂ��Ȃ邩�A�l���Ă݂܂��B�܂��A�A�C�B����Aφ����������ƁA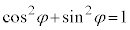 (�O�p���̏��������Q��)���A
(�O�p���̏��������Q��)���A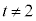 �C
�C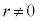 �C
�C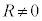 �Ƃ��āA
�Ƃ��āA 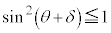 ���A
���A�������āA�}�`�I�l�@�Ɠ������ʂ������܂��B�������ł́A�������Ęr�s���Ōv�Z�ʼn����Ă��[���ɐ������Ԃɓ���Ǝv���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 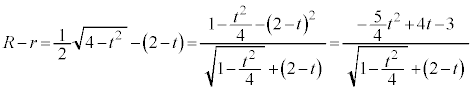
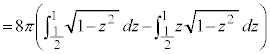
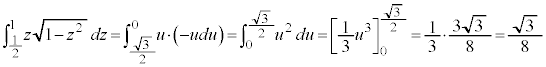
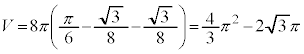 ......[��]
......[��]