���嗝�n���w'22�N�O��[6]
O�����_�Ƃ�����W���ʏ�ōl����B0�ȏ�̐���k�ɑ��āA�x�N�g��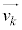 ��
��
�ƒ�߂�B�������Ƃ��\�Ɨ����ǂ����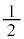 �̊m���ŏo��R�C����N���āA���W���ʏ�ɓ_
�̊m���ŏo��R�C����N���āA���W���ʏ�ɓ_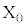 �C
�C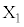 �C
�C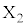 �C����C
�C����C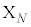 ���ȉ��̋K��(i)�C(ii)�ɏ]���Ē�߂�B
���ȉ��̋K��(i)�C(ii)�ɏ]���Ē�߂�B
(i) 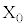 ��O�ɂ���B
��O�ɂ���B (ii) n��1�ȏ�N�ȉ��̐����Ƃ���B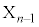 ����܂����Ƃ��A
����܂����Ƃ��A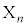 �����̂悤�ɒ�߂�B
�����̂悤�ɒ�߂�B �En��ڂ̃R�C�������ŕ\���o���ꍇ�A
�ɂ��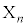 ���߂�B�������Ak��1��ڂ���n��ڂ܂ł̃R�C�������ŗ����o���Ƃ���B
���߂�B�������Ak��1��ڂ���n��ڂ܂ł̃R�C�������ŗ����o���Ƃ���B �En��ڂ̃R�C�������ŗ����o���ꍇ�A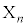 ��
��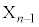 �ƒ�߂�B
�ƒ�߂�B (1) 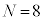 �Ƃ���B
�Ƃ���B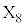 ��O�ɂ���m�������߂�B
��O�ɂ���m�������߂�B (2) 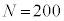 �Ƃ���B
�Ƃ���B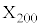 ��O�ɂ���A���A���v200��̃R�C�������ŕ\�����傤��r��o��m����
��O�ɂ���A���A���v200��̃R�C�������ŕ\�����傤��r��o��m����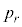 �Ƃ����B������
�Ƃ����B������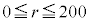 �ł���B
�ł���B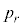 �����߂�B�܂�
�����߂�B�܂�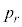 ���ő�ƂȂ�r�̒l�����߂�B
���ő�ƂȂ�r�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�j�̎q�̊Ԃɏ��̎q�����Ă����A�Ƃ������̗ޑ�Ȃ̂ł����Aꡂ��ɕ��G�ŁA(1)�ŃJ���N���ɋC�Â��Ȃ��ƁA(2)�ɐi�߂܂���B�ȉ��ł́A�J���N���ɋC�Â��܂ł��ׂ��������܂������A���ĂƂ��ẮA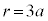 (
(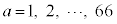 )�ƂȂ�ꍇ��[������]��1�܂Ƃ߂ɂ���J���N�������ȒP�ɋL�q����悤�ɂ��Ȃ��Ǝ��Ԃ�����Ȃ��Ȃ�܂��B�����Ă��ă]�N�]�N�����肾���ɐ[�݂ɂ͂܂��Ă��܂������ł����A���̖���D�悷��������i�ɂ͋߂��Ǝv���܂��B
)�ƂȂ�ꍇ��[������]��1�܂Ƃ߂ɂ���J���N�������ȒP�ɋL�q����悤�ɂ��Ȃ��Ǝ��Ԃ�����Ȃ��Ȃ�܂��B�����Ă��ă]�N�]�N�����肾���ɐ[�݂ɂ͂܂��Ă��܂������ł����A���̖���D�悷��������i�ɂ͋߂��Ǝv���܂��B
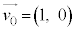
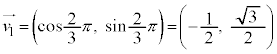
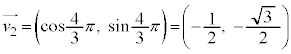
l ��0�ȏ�̐����Ƃ��āA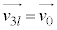 �C
�C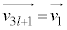 �C
�C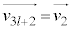 �@����@�@�ł��B
�@����@�@�ł��B
���W���ʏ�Ńx�N�g���ōl���Ă��悢�̂ł����A���f��������ōl���邱�Ƃɂ��܂��B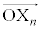 �ɑΉ����镡�f����
�ɑΉ����镡�f����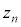 (
(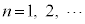 )�C
)�C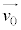 �ɑΉ����镡�f����1�C
�ɑΉ����镡�f����1�C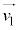 �ɑΉ����镡�f����
�ɑΉ����镡�f����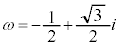 (1��3�捪��1�ł�)�C
(1��3�捪��1�ł�)�C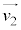 �ɑΉ����镡�f���́A
�ɑΉ����镡�f���́A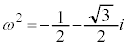 �ł��B
�ł��B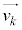 �ɑΉ����镡�f���́A
�ɑΉ����镡�f���́A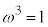 ���A�@�ɑΉ����āA
���A�@�ɑΉ����āA
�܂��A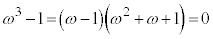 �C
�C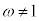 ���A
���A
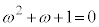 �@����B
�@����B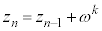 (k�Fn��ڂ܂łɗ����o����)�C�����o��ƁA
(k�Fn��ڂ܂łɗ����o����)�C�����o��ƁA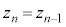 �C�Ƃ������Ƃł��B
�C�Ƃ������Ƃł��B
(1) n��ڂ܂łɗ����o����k�C�܂��Al��K����0�ȏ�̐����Ƃ��āA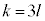 �ł���(mod���g���ď����ƁA
�ł���(mod���g���ď����ƁA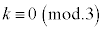 �C��]�����Q��)�Ԃɏo���\�̉�a (a��0�ȏ�̐���)�C
�C��]�����Q��)�Ԃɏo���\�̉�a (a��0�ȏ�̐���)�C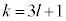 �ł���(
�ł���(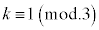 )�Ԃɕ\���o����b (b��0�ȏ�̐���)�C
)�Ԃɕ\���o����b (b��0�ȏ�̐���)�C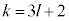 �ł���(
�ł���(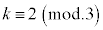 )�Ԃɕ\���o����c (c��0�ȏ�̐���)�Ƃ��܂��B
)�Ԃɕ\���o����c (c��0�ȏ�̐���)�Ƃ��܂��B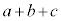 �͕\���o���A
�͕\���o���A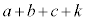 �̓R�C���𓊂����ɂȂ�܂��B
�̓R�C���𓊂����ɂȂ�܂��B �Ⴆ�A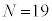 �Ƃ��āA�ȉ��̂悤�ɕ\�����o���Ƃ��܂��B�e�\�E���̉��ɏ�����Ă��鐔�́A�����܂łɏo�����̉ł��B�\���o���Ƃ��A���̉̉����ɁA���̉�3�Ŋ����鐔�̂Ƃ���'a'�C3�Ŋ����1�]��Ƃ���'b'�C3�Ŋ����2�]��Ƃ���'c'�Ə����Ă���܂��B
�Ƃ��āA�ȉ��̂悤�ɕ\�����o���Ƃ��܂��B�e�\�E���̉��ɏ�����Ă��鐔�́A�����܂łɏo�����̉ł��B�\���o���Ƃ��A���̉̉����ɁA���̉�3�Ŋ����鐔�̂Ƃ���'a'�C3�Ŋ����1�]��Ƃ���'b'�C3�Ŋ����2�]��Ƃ���'c'�Ə����Ă���܂��B
| �� | �\ | �� | �� | �\ | �\ | �� | �\ | �� | �\ | �� | �\ | �� | �� | �\ | �� | �� | �\ | �� |
| 1 | 1 | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 5 | 6 | 6 | 7 | 8 | 8 | 9 | 10 | 10 | 11 |
| b |
|
| a | a |
| b |
| c |
| a |
|
| c |
|
| b |
|
19��ڂ܂łŁA���̏o����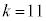 �C'a'�̌���
�C'a'�̌���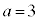 �C'b'�̌���
�C'b'�̌���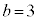 �C'c'�̌���
�C'c'�̌���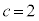 �ł��B
�ł��B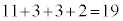 �ƂȂ��Ă��܂����A19��ڂ̃R�C�������ŁA�A�C�B���A
�ƂȂ��Ă��܂����A19��ڂ̃R�C�������ŁA�A�C�B���A �ƂȂ邽��O�ɖ߂��Ă��܂���Bn��ڂ̃R�C�������ŁA�A���A���f�����ʏ�ł́A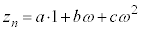 �ɗ��܂��B�B���A
�ɗ��܂��B�B���A �ƂȂ�̂ŁA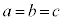 �łȂ�����A
�łȂ�����A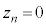 �Ƃ͂Ȃ�܂���B�܂�An��ڂ̃R�C��������O�ɖ߂��Ă���Ƃ��A
�Ƃ͂Ȃ�܂���B�܂�An��ڂ̃R�C��������O�ɖ߂��Ă���Ƃ��A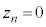 �ƂȂ邽�߂ɂ́A
�ƂȂ邽�߂ɂ́A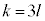 �ł���Ƃ��ɕ\���o���a�ƁA
�ł���Ƃ��ɕ\���o���a�ƁA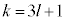 �ł���Ƃ��ɕ\���o���b�ƁA
�ł���Ƃ��ɕ\���o���b�ƁA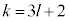 �ł���Ƃ��ɕ\���o���c�͓������Ȃ�܂��B���(��)
�ł���Ƃ��ɕ\���o���c�͓������Ȃ�܂��B���(��)
8��R�C������������ƁA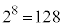 �ʂ�̕\���̏o��������܂��B
�ʂ�̕\���̏o��������܂��B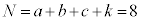 �̂Ƃ��ɁA
�̂Ƃ��ɁA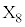 ��O�ɂ���A�܂�A
��O�ɂ���A�܂�A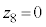 �ƂȂ�̂́A
�ƂȂ�̂́A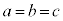 �ł����āA
�ł����āA 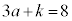 �@����C
�@����C�ƂȂ�Ƃ��ł��B
�����Ȃ�̂́A(i) 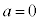 �C
�C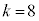 �C�܂��́A(ii)
�C�܂��́A(ii) 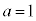 �C
�C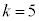 �C�܂��́A(iii)
�C�܂��́A(iii) 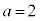 �C
�C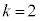 �̏ꍇ�Ɍ����܂��B
�̏ꍇ�Ɍ����܂��B
(i)�́A8��R�C�����������đS�������o��Ƃ������ƂŁA���̊m����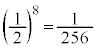 �ł�(�Ɨ����s�̊m�����Q��)�B
�ł�(�Ɨ����s�̊m�����Q��)�B
(ii)�́A8��R�C������������5�A3��\���o��A�Ƃ������ƂȂ̂ł����A���̑S�Ă̕\���̏o���ŏ����ɓK������A�Ƃ������Ƃł͂���܂���B
�Ⴆ�A�\�\�\�����������Əo�Ă��܂��ƁA��0��̂܂�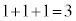 �Ɛi��ňȌ�5��̗��œ�����8��ڂ�O�ɖ߂��Ă��܂���B3��̕\���A
�Ɛi��ňȌ�5��̗��œ�����8��ڂ�O�ɖ߂��Ă��܂���B3��̕\���A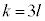 �ƂȂ�Ƃ���1��\���o�āA
�ƂȂ�Ƃ���1��\���o�āA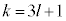 �̂Ƃ���1��\���o�āA
�̂Ƃ���1��\���o�āA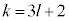 �̂Ƃ��ɕ\��1��o�邱�Ƃ������ł��B
�̂Ƃ��ɕ\��1��o�邱�Ƃ������ł��B
�Ⴆ�A1��ڂɕ\���o��ƁA���̎��_�ŗ��̉�0 (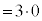 )�Ȃ̂ŁA
)�Ȃ̂ŁA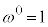 �i�݂܂��B2��ڂɗ����o�āA3��ڂɕ\���o��ƁA���̎��_�ŗ��̉�1 (
�i�݂܂��B2��ڂɗ����o�āA3��ڂɕ\���o��ƁA���̎��_�ŗ��̉�1 (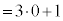 )�Ȃ̂ŁA
)�Ȃ̂ŁA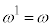 �i�݁A
�i�݁A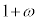 �ɗ��܂��B4��ڂɗ����o�āA5��ڂɕ\���o��ƁA���̎��_�ŗ��̉�2 (
�ɗ��܂��B4��ڂɗ����o�āA5��ڂɕ\���o��ƁA���̎��_�ŗ��̉�2 (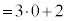 )�Ȃ̂ŁA
)�Ȃ̂ŁA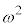 �i��ŁA
�i��ŁA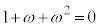 �ɗ���̂ŁAO�ɖ߂�܂��B���̌�A6��ځA7��ځA8��ڂɗ����o��ƁAO�ɋ�������̂ŁA8��ڂ�O�ɂ��܂��B�܂�A�\���\���\�������Əo���O�ɂ��܂��B1��ڂɕ\���o��(���̉�0)�ꍇ�Ɍ��炸�A1�i���\�́A���̉�3��̂Ƃ��A�Ⴆ�A���\���\���A�Əo�Ă���\���o��Ƃ��ɂ�
�ɗ���̂ŁAO�ɖ߂�܂��B���̌�A6��ځA7��ځA8��ڂɗ����o��ƁAO�ɋ�������̂ŁA8��ڂ�O�ɂ��܂��B�܂�A�\���\���\�������Əo���O�ɂ��܂��B1��ڂɕ\���o��(���̉�0)�ꍇ�Ɍ��炸�A1�i���\�́A���̉�3��̂Ƃ��A�Ⴆ�A���\���\���A�Əo�Ă���\���o��Ƃ��ɂ�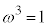 �i�݂܂��B���̌�A���������āA���\���\���\�����Əo��ꍇ���A8��ڂ�O�ɂ��܂��B
�i�݂܂��B���̌�A���������āA���\���\���\�����Əo��ꍇ���A8��ڂ�O�ɂ��܂��B
�܂�A�u�\���\���\�������v�ł��u���\���\���\�����v�ł��A8��ڂ�O�ɂ��܂��B�u�\���\���\�������v�Ɓu���\���\���\�����v��3��̕\�̂����Aω�i���\��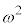 �i���\����蕥���Ă݂܂��B7��ڂ�8��ڂ̗���O�ɂ���܂܂ɂȂ�̂ŁA����������čl����ƁA1�i���\�̓�����́A�u�\������ �����v�Ɓu�������\ �����v�ƂȂ�A�Ō��2��̗����ʂɂ��āA�\��[������]�̕��ו����l����Ηǂ����Ƃ��킩��܂��Bω�i���\�����l�ɁA���̉�1��̂Ƃ���4��̂Ƃ�������(�C���A����7��Ƃ������Ƃ͂���܂���)�̂ł����A�u�\���\���\�������v�Ɓu�\�����\�����\���v���A1�i���\��
�i���\����蕥���Ă݂܂��B7��ڂ�8��ڂ̗���O�ɂ���܂܂ɂȂ�̂ŁA����������čl����ƁA1�i���\�̓�����́A�u�\������ �����v�Ɓu�������\ �����v�ƂȂ�A�Ō��2��̗����ʂɂ��āA�\��[������]�̕��ו����l����Ηǂ����Ƃ��킩��܂��Bω�i���\�����l�ɁA���̉�1��̂Ƃ���4��̂Ƃ�������(�C���A����7��Ƃ������Ƃ͂���܂���)�̂ł����A�u�\���\���\�������v�Ɓu�\�����\�����\���v���A1�i���\��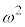 �i���\����蕥���ƁA�u�� �\������ ���v�Ɓu�� �������\ ���v���A���[�̗���ʂɂ��āA�\��[������]�̕��ו����l����Ηǂ����ƂɂȂ�܂��B
�i���\����蕥���ƁA�u�� �\������ ���v�Ɓu�� �������\ ���v���A���[�̗���ʂɂ��āA�\��[������]�̕��ו����l����Ηǂ����ƂɂȂ�܂��B
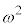 �i���\�����l�ɁA�u���� �\�������v�Ɓu���� �������\�v�ŁA�ŏ���2��̗���ʂɂ��āA�\��[������]�̕��ו����l����Ηǂ����ƂɂȂ�܂��B
�i���\�����l�ɁA�u���� �\�������v�Ɓu���� �������\�v�ŁA�ŏ���2��̗���ʂɂ��āA�\��[������]�̕��ו����l����Ηǂ����ƂɂȂ�܂��B
�������āA�\�Ɨ��̕��ו����A��3����܂Ƃ߂�[������]�Ƃ��čl���A���̉�3�Ŋ�����3�ʂ�̗]��̊e�X�ɂ��āA1�i���\��[������]�̕��ו��Aω�i���\��[������]�̕��ו��A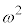 �i���\��[������]�̕��ו���ʁX�ɐ����邱�Ƃɂ��AO�ɖ߂�R�C�������̏ꍇ�̐����l���邱�Ƃ��ł��܂��B����3��̕��ו��́A���ꂼ���Ɨ��ŁA�\���̏o���S�̂̊m���́A3��̕��ו��̊m����������悢���Ƃɒ��ӂ��Ă�������(�ώ��ہE�a���ہE�]�������Q��)�B���������̖��̃J���N���̊�(����)�ł��B
�i���\��[������]�̕��ו���ʁX�ɐ����邱�Ƃɂ��AO�ɖ߂�R�C�������̏ꍇ�̐����l���邱�Ƃ��ł��܂��B����3��̕��ו��́A���ꂼ���Ɨ��ŁA�\���̏o���S�̂̊m���́A3��̕��ו��̊m����������悢���Ƃɒ��ӂ��Ă�������(�ώ��ہE�a���ہE�]�������Q��)�B���������̖��̃J���N���̊�(����)�ł��B
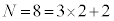 �̂Ƃ��ɂ́A�]��2�̗�2����A1�i�ޕ\���l����Ƃ��ɂ́A1��ڂ̕\��1�i�ނ悤�ɁA�Ō��[����]�ł܂Ƃ߁Aω�i�ޕ\���l����Ƃ��ɂ́A�ŏ���[��]��1��(���̌�̕\��ω�i�݂܂�)�A�Ō��[��]��1��ƐU�蕪���A
�̂Ƃ��ɂ́A�]��2�̗�2����A1�i�ޕ\���l����Ƃ��ɂ́A1��ڂ̕\��1�i�ނ悤�ɁA�Ō��[����]�ł܂Ƃ߁Aω�i�ޕ\���l����Ƃ��ɂ́A�ŏ���[��]��1��(���̌�̕\��ω�i�݂܂�)�A�Ō��[��]��1��ƐU�蕪���A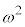 �i�ޕ\���l����Ƃ��ɂ͍ŏ���[����](���̌�̕\��
�i�ޕ\���l����Ƃ��ɂ͍ŏ���[����](���̌�̕\��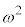 �i�݂܂�)�ł܂Ƃ߂čl���܂��B�@���(����)
�i�݂܂�)�ł܂Ƃ߂čl���܂��B�@���(����)
1�i�ނƂ�(���̉�3�Ŋ���Ɨ]���0)�̕\��1�Ə������Ƃɂ���ƁA 1[������][����]
[������]1[����]
��2�ʂ肠��܂��B�ܘ_�A[������]�̗��Ɨ��̊Ԃɕ\���o��(���̕\�ł́A1�i�ނ��Ƃ͂���܂���)���Ƃ����蓾�܂��B[������]�Ə����̂́A1�i�ނƂ��̕\�ɑ��Ă����ł��B
ω�i�ނƂ�(���̉�3�Ŋ���Ɨ]���1)�̕\��ω�Ə������Ƃɂ���ƁA
[��]ω[������][��]
[��][������]ω[��]
��2�ʂ肠��܂��B[������]�̗��Ɨ��̊Ԃɕ\���o��(���̕\�ł́Aω�i�ނ��Ƃ͂���܂���)���Ƃ����蓾��̂͐�̏ꍇ�Ɠ��l�ł��B
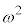 �i�ނƂ�(���̉�3�Ŋ���Ɨ]���1)�̕\��
�i�ނƂ�(���̉�3�Ŋ���Ɨ]���1)�̕\��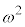 �Ə������Ƃɂ���ƁA
�Ə������Ƃɂ���ƁA [����]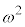 [������]
[������]
[����][������]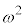
��2�ʂ肠��܂��B[������]�̗��Ɨ��̊Ԃɕ\���o��(���̕\�ł́A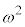 �i�ނ��Ƃ͂���܂���)���Ƃ����蓾�܂��B
�i�ނ��Ƃ͂���܂���)���Ƃ����蓾�܂��B
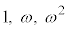 �̂�����ɂ��Ă��A[������]��1�܂Ƃ߂ɂ���2�ʂ肸����܂��B�܂�A3��\���o��O�ɖ߂�̂́A
�̂�����ɂ��Ă��A[������]��1�܂Ƃ߂ɂ���2�ʂ肸����܂��B�܂�A3��\���o��O�ɖ߂�̂́A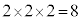 �ʂ肠��A���̊m���́A
�ʂ肠��A���̊m���́A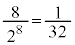 �ł��B
�ł��B (iii)��1�ړ�����\���Aω�ړ�����\���A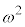 �ړ�����\��2�o��A�Ƃ������Ƃł����A�����Ȃ�̂́A1��ڂ�2��ڂɕ\���o�āA��0��Ȃ̂�1����2��i�݁A3��ڂɗ��A4��ڂ�5��ڂɕ\���o�āA��1��Ȃ̂ŁAω����2��i�݁A6��ڂɗ����o�āA7��ڂ�8��ڂɕ\���o�āA��2��Ȃ̂ŁA
�ړ�����\��2�o��A�Ƃ������Ƃł����A�����Ȃ�̂́A1��ڂ�2��ڂɕ\���o�āA��0��Ȃ̂�1����2��i�݁A3��ڂɗ��A4��ڂ�5��ڂɕ\���o�āA��1��Ȃ̂ŁAω����2��i�݁A6��ڂɗ����o�āA7��ڂ�8��ڂɕ\���o�āA��2��Ȃ̂ŁA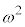 ����2��i�݁A
����2��i�݁A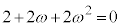 �ƂȂ���O�ɖ߂�ꍇ�����ł��B���̊m���́A
�ƂȂ���O�ɖ߂�ꍇ�����ł��B���̊m���́A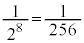 �ł��B
�ł��B �ȏ���A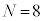 �̂Ƃ��A
�̂Ƃ��A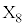 ��O�ɂ���m���́A
��O�ɂ���m���́A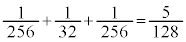 ......[��]
......[��]
(2) 200��R�C������������ƁA�\���̏o����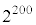 �ʂ肠��܂��B(1)�Ɠ��l�ɁAl��0�ȏ�̐����Ƃ��āA200��܂łɗ��̏o���k�ɂ��āA
�ʂ肠��܂��B(1)�Ɠ��l�ɁAl��0�ȏ�̐����Ƃ��āA200��܂łɗ��̏o���k�ɂ��āA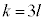 �C
�C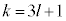 �C
�C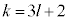 �̊Ԃɂ��ꂼ��\���o���a�Cb�Cc�Ƃ���ƁA
�̊Ԃɂ��ꂼ��\���o���a�Cb�Cc�Ƃ���ƁA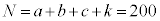 �C
�C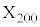 ��O�ɂ��邽�߂ɂ́A(1)(��)���A
��O�ɂ��邽�߂ɂ́A(1)(��)���A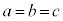 �ł����āA�\���o���
�ł����āA�\���o���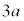 (
(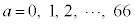 )�ŁA
)�ŁA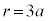 �łȂ���A
�łȂ���A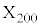 ��O�ɂ��邱�Ƃ͂Ȃ��A
��O�ɂ��邱�Ƃ͂Ȃ��A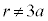 �Ȃ�
�Ȃ�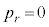 �ł��B
�ł��B �܂��A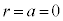 �̂Ƃ��A����200�����A�Ƃ������ƂŁA���̊m���́A
�̂Ƃ��A����200�����A�Ƃ������ƂŁA���̊m���́A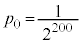
���āA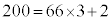 �ł��B200��3�Ŋ����2�]��̂ŁA��2����A(1)(ii)(����)�Ɠ��l�ɍŏ��ƍŌ�ɐU�蕪���A
�ł��B200��3�Ŋ����2�]��̂ŁA��2����A(1)(ii)(����)�Ɠ��l�ɍŏ��ƍŌ�ɐU�蕪���A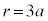 (
(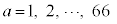 )�̂Ƃ��A(1)(ii)�ōl�����悤�ɁA��3���[������]�Ƃ܂Ƃ߂čl���܂��B
)�̂Ƃ��A(1)(ii)�ōl�����悤�ɁA��3���[������]�Ƃ܂Ƃ߂čl���܂��B
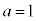 �̂Ƃ��A
�̂Ƃ��A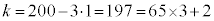 ���A1�i��(���̉�3�Ŋ���Ɨ]���0)�\������̂́A
���A1�i��(���̉�3�Ŋ���Ɨ]���0)�\������̂́A ��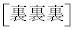 �̑O��ŁA66�J����1��I�Ԃƍl���A
�̑O��ŁA66�J����1��I�Ԃƍl���A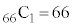 �ʂ�(�g�ݍ��킹���Q��)����܂��Bω�i��(���̉�3�Ŋ���Ɨ]���1)�\������̂́A
�ʂ�(�g�ݍ��킹���Q��)����܂��Bω�i��(���̉�3�Ŋ���Ɨ]���1)�\������̂́A ��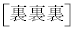 �̑O��ŁA��͂�
�̑O��ŁA��͂�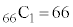 �ʂ肠��܂��B
�ʂ肠��܂��B
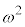 �i��(���̉�3�Ŋ���Ɨ]���2)�\������̂́A
�i��(���̉�3�Ŋ���Ɨ]���2)�\������̂́A ��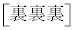 �̑O��ŁA��͂�
�̑O��ŁA��͂�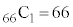 �ʂ肠��܂��B
�ʂ肠��܂��B
������A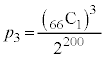
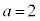 �̂Ƃ��A
�̂Ƃ��A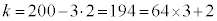 ���A1�i��(���̉�3�Ŋ���Ɨ]���0)�\��2����̂́A
���A1�i��(���̉�3�Ŋ���Ɨ]���0)�\��2����̂́A ��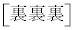 �̑O��ŁA64�J����
�̑O��ŁA64�J����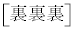 ��2�J����1�i�ޕ\�̕��ו��́A���킹��66�J���̂ǂ�2�J����\�ɂ��邩�ƍl���āA
��2�J����1�i�ޕ\�̕��ו��́A���킹��66�J���̂ǂ�2�J����\�ɂ��邩�ƍl���āA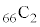 �ʂ�(�g�ݍ��킹���Q��)����܂��Bω�i��(���̉�3�Ŋ���Ɨ]���1)�\��2����̂́A
�ʂ�(�g�ݍ��킹���Q��)����܂��Bω�i��(���̉�3�Ŋ���Ɨ]���1)�\��2����̂́A ��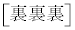 �̑O��ŁA��͂�
�̑O��ŁA��͂�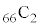 �ʂ肠��܂��B
�ʂ肠��܂��B
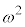 �i��(���̉�3�Ŋ���Ɨ]���2)�\������̂́A
�i��(���̉�3�Ŋ���Ɨ]���2)�\������̂́A ��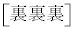 �̑O��ŁA��͂�
�̑O��ŁA��͂�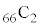 �ʂ肠��܂��B
�ʂ肠��܂��B
������A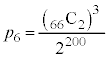
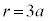 (
(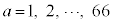 )�̂Ƃ��A
)�̂Ƃ��A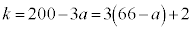 ���A1�i��(���̉�3�Ŋ���Ɨ]���0)�\��a����̂́A
���A1�i��(���̉�3�Ŋ���Ɨ]���0)�\��a����̂́A ��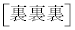 �̑O��ŁA
�̑O��ŁA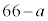 �J����
�J����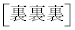 ��a�J����1�i�ޕ\�̕��ו��́A���킹��66�J���̂ǂ�a�J����\�ɂ��邩�ƍl���āA
��a�J����1�i�ޕ\�̕��ו��́A���킹��66�J���̂ǂ�a�J����\�ɂ��邩�ƍl���āA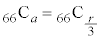 �ʂ�(�g�ݍ��킹���Q��)����܂�([������]��[������]�̊Ԃ�1�i�ޕ\���������Ă��悢���Ƃɒ���)�Bω�i��(���̉�3�Ŋ���Ɨ]���1)�\��a����̂́A
�ʂ�(�g�ݍ��킹���Q��)����܂�([������]��[������]�̊Ԃ�1�i�ޕ\���������Ă��悢���Ƃɒ���)�Bω�i��(���̉�3�Ŋ���Ɨ]���1)�\��a����̂́A ��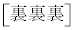 �̑O��ŁA��͂�
�̑O��ŁA��͂�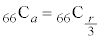 �ʂ肠��܂��B
�ʂ肠��܂��B
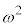 �i��(���̉�3�Ŋ���Ɨ]���2)�\��a����̂́A
�i��(���̉�3�Ŋ���Ɨ]���2)�\��a����̂́A ��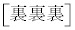 �̑O��ŁA��͂�
�̑O��ŁA��͂�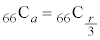 �ʂ肠��܂��B
�ʂ肠��܂��B
������A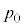 ���܂߁A
���܂߁A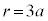 (
(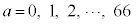 )�̂Ƃ��A
)�̂Ƃ��A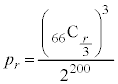 �C
�C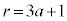 �C
�C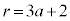 �̂Ƃ��A
�̂Ƃ��A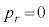 ......[��]
......[��] ���A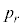 ���ő�Ƃ���r�́A
���ő�Ƃ���r�́A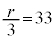 ���A
���A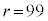 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
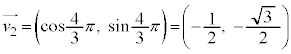
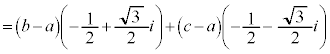
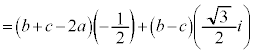



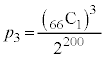


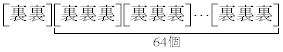
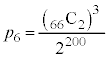



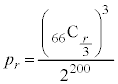 �C
�C