���嗝�n���w'22�N�O��[2]
����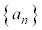 �����̂悤�ɒ�߂�B
�����̂悤�ɒ�߂�B
(1) ���̐���n��3�̔{���̂Ƃ��A ��5�̔{���ƂȂ邱�Ƃ������B
��5�̔{���ƂȂ邱�Ƃ������B (2) k�Cn�𐳂̐����Ƃ���B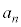 ��
��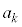 �̔{���ƂȂ邽�߂̕K�v�\��������k�Cn��p���ĕ\���B
�̔{���ƂȂ邽�߂̕K�v�\��������k�Cn��p���ĕ\���B (3) 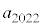 ��
�� �̍ő�������߂�B
�̍ő�������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
������̍ŏ��̕��ׂ悤�Ƃ��āA �C
�C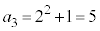 �C
�C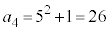 �C
�C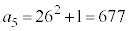 �C�Ƃ���čs���ƁA
�C�Ƃ���čs���ƁA �C
�C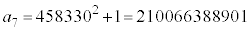 �C�ƁA���܂������ƂɂȂ��Ă��܂��܂��B(3)�ŁA
�C�ƁA���܂������ƂɂȂ��Ă��܂��܂��B(3)�ŁA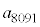 �ƂȂ�ƁA�����ł����V���w�I���l�ł��B(3)�́A221��51���ő���������߂�A�ƌ���ꂽ�Ƃ��ɁA221��51��4���܂�17�ƂȂ�Ƃ��납��51��17�̍ő�����l����̂Ɠ����悤�ɂ��܂��B
�ƂȂ�ƁA�����ł����V���w�I���l�ł��B(3)�́A221��51���ő���������߂�A�ƌ���ꂽ�Ƃ��ɁA221��51��4���܂�17�ƂȂ�Ƃ��납��51��17�̍ő�����l����̂Ɠ����悤�ɂ��܂��B
(1) 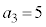 ��5�̔{���ł��B
��5�̔{���ł��B m�����R���Ƃ��܂��B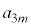 ��5�̔{�����Ƃ��āA
��5�̔{�����Ƃ��āA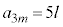 (l�F����)�Ƃ����ƁA
(l�F����)�Ƃ����ƁA 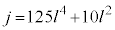 �Ƃ����ƁA
�Ƃ����ƁA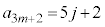
����āA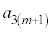 ��5�̔{���ł��B
��5�̔{���ł��B
��������w�I�A�[�@�ɂ��A�S�Ă̎��R��m�ɂ��āA�܂�C���̐���n��3�̔{���ł���Ƃ��A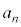 ��5�̔{���ł��B
��5�̔{���ł��B
�ʉ��Dmod�L��(��]�����Q��)��p���ē��Ă������ƈȉ��̂悤�ɊȌ��ɏ������Ƃ��ł��܂��B m�����R���Ƃ��āA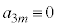 (mod. 5)�������B
(mod. 5)�������B
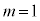 �̂Ƃ��A
�̂Ƃ��A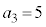 ��萬�藧�B
��萬�藧�B
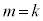 �̂Ƃ��A
�̂Ƃ��A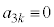 (mod. 5)�����肷��ƁA
(mod. 5)�����肷��ƁA 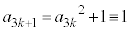 (mod. 5)
(mod. 5)
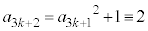 (mod. 5)
(mod. 5)
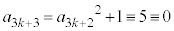 (mod. 5)����āA
(mod. 5)����āA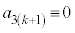 (mod. 5)�ƂȂ�A
(mod. 5)�ƂȂ�A �̂Ƃ������藧�B
�̂Ƃ������藧�B���w�I�A�[�@�ɂ��Am�����R���Ƃ��āA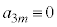 (mod. 5)�����藧�B
(mod. 5)�����藧�B
�����A���̐���n��3�̔{���̂Ƃ��A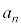 ��5�̔{���ƂȂ�B
��5�̔{���ƂȂ�B
(2) k�����R���Ƃ��āA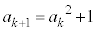 �C
�C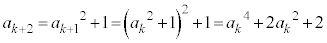 �C
�C 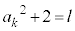 (l�F����)�Ƃ����ƁA
(l�F����)�Ƃ����ƁA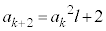
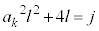 (j�F����)�Ƃ����ƁA
(j�F����)�Ƃ����ƁA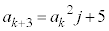
�Ƃ���čs���ƁA �C
�C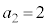 �C
�C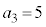 �C
�C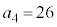 �C����Ȃ̂ŁA
�C����Ȃ̂ŁA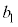 (
(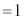 )�C
)�C �C����𐮐��Ƃ��āA
�C����𐮐��Ƃ��āA �ƂȂ��Ă��邱�Ƃ��킩��܂��B
�����ŁAk�����R���A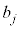 �𐮐��Ƃ��āA
�𐮐��Ƃ��āA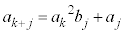 �������܂��B
�������܂��B
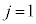 �̂Ƃ��́A
�̂Ƃ��́A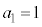 ���A
���A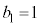 �Ƃ��āA
�Ƃ��āA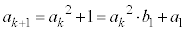
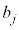 �𐮐��Ƃ��āA
�𐮐��Ƃ��āA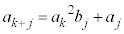 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA 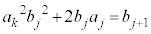 �@����@�@�Ƃ����
�@����@�@�Ƃ����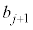 �͐����ł����āA
�͐����ł����āA ���A
���A�Ə����܂��B����āAj�����R���Ƃ��āA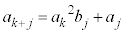 �@����A�@�Ə����邱�Ƃ�������܂����B
�@����A�@�Ə����邱�Ƃ�������܂����B
�@��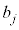 �͎��R��k�ɂ��ˑ�����̂ŁA
�͎��R��k�ɂ��ˑ�����̂ŁA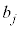 �����߂�
�����߂�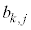 �Ə��������ƁA�@��
�Ə��������ƁA�@��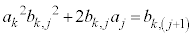 �Ə��������āA�A�́A
�Ə��������āA�A�́A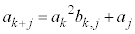 �@����B
�@����B
�ƂȂ�܂��B
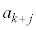 ��
��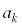 �̔{���ł��邽�߂ɂ́A�B���
�̔{���ł��邽�߂ɂ́A�B���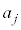 ��
��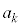 �̔{���ł��邱�Ƃ��K�v�ł��B
�̔{���ł��邱�Ƃ��K�v�ł��B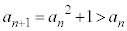 ���A����
���A����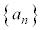 �͒P�������Ȑ���ŁA
�͒P�������Ȑ���ŁA �̂Ƃ�
�̂Ƃ�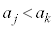 (���̂Ƃ��A
(���̂Ƃ��A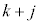 ��k�̔{���łȂ��A
��k�̔{���łȂ��A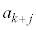 ��
��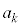 �̔{���ɂȂ�܂���)�C
�̔{���ɂȂ�܂���)�C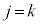 �̂Ƃ�
�̂Ƃ�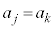 �C
�C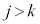 �̂Ƃ�
�̂Ƃ�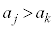 ���A
���A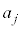 ��
��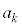 �̔{���ƂȂ�ŏ��̎��R��j��k�ł��B
�̔{���ƂȂ�ŏ��̎��R��j��k�ł��B
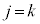 �̂Ƃ��A
�̂Ƃ��A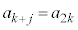 �́A�B���A
�́A�B���A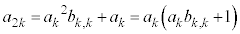 �ƂȂ�A
�ƂȂ�A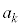 �̔{���ł��B������
�̔{���ł��B������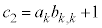 �͐����ŁA
�͐����ŁA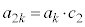 �ƂȂ�܂�(
�ƂȂ�܂�(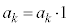 ���
���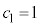 �Ƃ��܂��B
�Ƃ��܂��B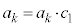 �ł�)�B
�ł�)�B
���l�ɇB���A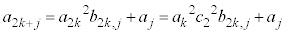 �@����C�@��
�@����C�@��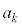 �̔{���ł��邽�߂ɂ́A
�̔{���ł��邽�߂ɂ́A ��
��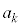 �̔{���ł��邱�Ƃ��K�v�ŁA�����Ȃ�ŏ��̎��R��j��
�̔{���ł��邱�Ƃ��K�v�ŁA�����Ȃ�ŏ��̎��R��j��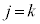 �ł��B
�ł��B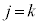 �̂Ƃ��A
�̂Ƃ��A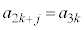 �́A�C���A
�́A�C���A �́A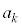 �̔{���ł��B������
�̔{���ł��B������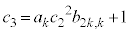 �͐����ŁA
�͐����ŁA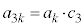 �ƂȂ�܂��B
�ƂȂ�܂��B
������J��Ԃ��ƁAi�����R���Ƃ��A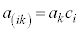 (
(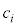 �͐����A
�͐����A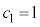 )�Ƃ�����Ɖ��肷��ƁA�B���A
)�Ƃ�����Ɖ��肷��ƁA�B���A 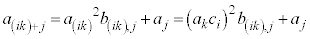 �@����D
�@����D��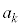 �̔{���ł��邽�߂ɂ́A
�̔{���ł��邽�߂ɂ́A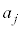 ��
��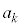 �̔{���ł��邱�Ƃ��K�v�ŁA�����Ȃ�ŏ��̎��R��j��
�̔{���ł��邱�Ƃ��K�v�ŁA�����Ȃ�ŏ��̎��R��j��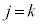 �ł���A
�ł���A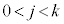 �̏ꍇ�ɂ�
�̏ꍇ�ɂ�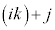 ��k�̔{���łȂ��A
��k�̔{���łȂ��A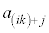 ��
��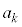 �̔{���ł͂���܂���B
�̔{���ł͂���܂���B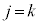 �̂Ƃ��A
�̂Ƃ��A �́A�D���A
�́A�D���A 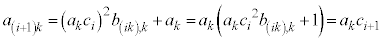 �@(
�@(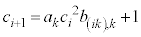 �͐����ł�)
�͐����ł�)�́A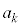 �̔{���ł��B
�̔{���ł��B
����āA���w�I�A�[�@�ɂ��A�S�Ă̎��R��i�ɂ��āA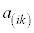 ��
��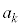 �̔{���A�܂�A
�̔{���A�܂�A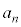 ��
��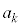 �̔{���ƂȂ邽�߂ɂ́Ai�����R���Ƃ��āA
�̔{���ƂȂ邽�߂ɂ́Ai�����R���Ƃ��āA �ƂȂ邱�Ƃ��K�v�ŁAn��k�̔{���łȂ��Ƃ���
�ƂȂ邱�Ƃ��K�v�ŁAn��k�̔{���łȂ��Ƃ���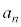 ��
��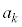 �̔{���ł͂���܂���B�t�ɁA
�̔{���ł͂���܂���B�t�ɁA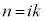 �̂Ƃ��A
�̂Ƃ��A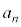 ��
��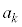 �̔{���ł��B
�̔{���ł��B
�ȏ���Ak�Cn�𐳂̐����Ƃ��āA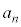 ��
��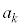 �̔{���ƂȂ��K�v�\�������́A�un��k�̔{���ł��邱�Ɓv ......[��]
�̔{���ƂȂ��K�v�\�������́A�un��k�̔{���ł��邱�Ɓv ......[��] �ʉ��D(2)����L�̂͂��߂̕��̍l�@�ŇB�������Ă���̂ŁA�B���A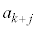 ��
��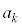 �Ŋ����
�Ŋ���� �]��ƌ��āAmod�L��(��]�����Q��)���g���āA
�]��ƌ��āAmod�L��(��]�����Q��)���g���āA 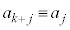 (mod.
(mod. 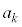 )�@(��)
)�@(��)�������Ƃ������j�������܂��B
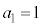 ���A
���A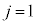 �̂Ƃ��A
�̂Ƃ��A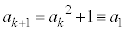 (mod.
(mod. 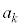 )
)
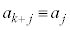 (mod.
(mod. 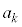 )�����肵�āA
)�����肵�āA ���A
���A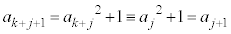 (mod.
(mod. 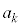 )�ƂȂ�̂ŁA(��)�����藧���܂��B(��)���A
)�ƂȂ�̂ŁA(��)�����藧���܂��B(��)���A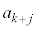 ��
��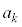 �Ŋ�����̂́A
�Ŋ�����̂́A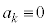 (mod.
(mod. 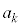 )���
)���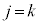 �̂Ƃ��ŁA���̂Ƃ��A
�̂Ƃ��ŁA���̂Ƃ��A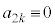 (mod.
(mod. 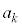 )�C���l�ɁA
)�C���l�ɁA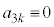 �C����C������An��k�̔{���̂Ƃ��A
�C����C������An��k�̔{���̂Ƃ��A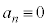 (mod.
(mod. 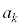 )�������܂��B�܂��A��L�Ɠ��l�ɁA
)�������܂��B�܂��A��L�Ɠ��l�ɁA (mod. k)�ȊO�̏ꍇ�ɂ�
(mod. k)�ȊO�̏ꍇ�ɂ�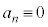 (mod.
(mod. 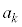 )�Ƃ͂Ȃ�Ȃ����Ƃ������K�v������܂��B
)�Ƃ͂Ȃ�Ȃ����Ƃ������K�v������܂��B
(3) 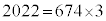 ��3�̔{���ł��B�܂��A
��3�̔{���ł��B�܂��A �ł��B(2)���A
�ł��B(2)���A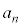 ��
��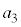 �̔{���ƂȂ�K�v�\��������n��3�̔{���ł��邱�Ƃł��B�܂��A
�̔{���ƂȂ�K�v�\��������n��3�̔{���ł��邱�Ƃł��B�܂��A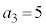 ��5�̔{���ł���25�̔{���ł͂���܂���B�����ŁAj��3�̔{���Ƃ��āA
��5�̔{���ł���25�̔{���ł͂���܂���B�����ŁAj��3�̔{���Ƃ��āA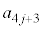 �ׂ邱�ƂɂȂ�܂��B
�ׂ邱�ƂɂȂ�܂��B (2)�B�ɂ����āAk��3�̔{���A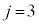 �Ƃ��āA
�Ƃ��āA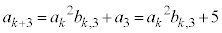 �@����E
�@����E
������A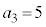 ��5�̔{���ł���25�̔{���ł͂Ȃ��A
��5�̔{���ł���25�̔{���ł͂Ȃ��A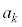 ��5�̔{������25�̔{���ł͂Ȃ��Ɖ��肷��ƁA
��5�̔{������25�̔{���ł͂Ȃ��Ɖ��肷��ƁA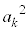 ��25�̔{���ł����A
��25�̔{���ł����A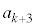 ��5�̔{������25�̔{���ɂ͂Ȃ�܂���B
��5�̔{������25�̔{���ɂ͂Ȃ�܂���B
�]���āA���ׂĂ�3�̔{��n�ɂ��āA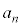 ��5�̔{������25�̔{���ł͂���܂���B���(����)
��5�̔{������25�̔{���ł͂���܂���B���(����)
j��3�̔{���Ƃ��āA�ĂчB��p���āA �E��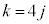 �Ƃ��āA
�Ƃ��āA 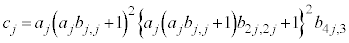 �Ƃ����ƁA
�Ƃ����ƁA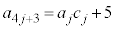
�܂�A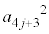 ��
��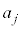 �Ŋ����25�]��̂ł����A����́A
�Ŋ����25�]��̂ł����A����́A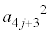 ��
��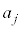 �̍ő�����A
�̍ő�����A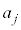 ��25�̍ő���Ɉ�v���邱�Ƃ��Ӗ����܂�(Euclid�̌ݏ��@���Q��)�B(����)���Aj��3�̔{���̂Ƃ��A
��25�̍ő���Ɉ�v���邱�Ƃ��Ӗ����܂�(Euclid�̌ݏ��@���Q��)�B(����)���Aj��3�̔{���̂Ƃ��A ��5�̔{������25�̔{���ł͂Ȃ��̂ŁA
��5�̔{������25�̔{���ł͂Ȃ��̂ŁA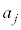 ��25�̍ő����5�C�����A
��25�̍ő����5�C�����A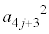 ��
��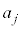 �̍ő����5�ł��B
�̍ő����5�ł��B
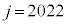 �Ƃ��āA
�Ƃ��āA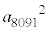 ��
��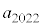 �̍ő���́A5 ......[��]
�̍ő���́A5 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B