���嗝�n���w'25�N�O��[4]
���̖₢�ł́A0�ȏ�̐�����2��ɂȂ鐔�����ƌĂԁBa�𐳂̐����Ƃ��A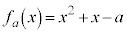 �Ƃ����B
�Ƃ����B
(1) n�𐳂̐����Ƃ���B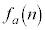 ���������Ȃ�A
���������Ȃ�A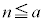 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B
(2) 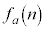 ���������ƂȂ鐳�̐���n�̌���
���������ƂȂ鐳�̐���n�̌���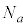 �Ƃ����B���̏���(i)�C(ii)�����l�ł��邱�Ƃ������B
�Ƃ����B���̏���(i)�C(ii)�����l�ł��邱�Ƃ������B (i) 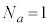 �ł���B
�ł���B (ii) 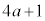 �͑f���ł���B
�͑f���ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ƃ����ɂ��������̖��ł����A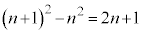 ���A
���A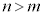 �Ƃ��āA
�Ƃ��āA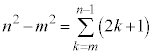 ���l�^�ɂ������ł��B�ȉ��̉͂������甭�z���Ă��܂��B
���l�^�ɂ������ł��B�ȉ��̉͂������甭�z���Ă��܂��B
(2)�́A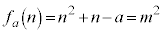 �̂Ƃ�
�̂Ƃ�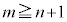 �͕������ł��B
�͕������ł��B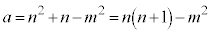 �Ƃ����̂́A
�Ƃ����̂́A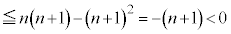 �ȊO��
�ȊO��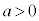 ���������ɂȂ邱�Ƃ͂Ȃ��A�Ƃ������Ƃł��B
���������ɂȂ邱�Ƃ͂Ȃ��A�Ƃ������Ƃł��B
(1) m��0�ȏ�̐����Ƃ��āA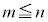 �@����@
�@����@ �ƂȂ����Ƃ��܂��B
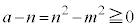 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA 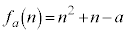 �@(n�͐��̐���)
�@(n�͐��̐���)�����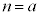 �ɖ�������̂ŁA
�ɖ�������̂ŁA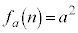 �ł��B�@����A
�ł��B�@����A
�@���A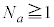 �@��
�@�� 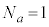
(2) 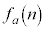 ���������̂Ƃ�(1)���
���������̂Ƃ�(1)���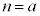 �ł����A
�ł����A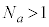 �̂Ƃ�
�̂Ƃ�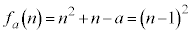 �́A
�́A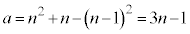 �ƂȂ蕽�����ɂȂ�̂ŁA
�ƂȂ蕽�����ɂȂ�̂ŁA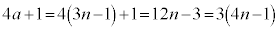 �ł��B
�ł��B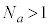 �Ƃ����̂́A
�Ƃ����̂́A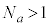 �������ƂȂ鐳�̐���n��
�������ƂȂ鐳�̐���n��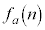 �ȊO�ɑ��݂��Ȃ��A�Ƃ������Ƃł��B�@���(��)
�ȊO�ɑ��݂��Ȃ��A�Ƃ������Ƃł��B�@���(��) �܂�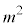 �ƂȂ�ꍇ�ŁA�A���A�Ⴆ��
�ƂȂ�ꍇ�ŁA�A���A�Ⴆ��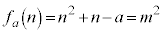 �̏ꍇ�ׂĂ݂܂��B
�̏ꍇ�ׂĂ݂܂��B ���̂Ƃ��A
�́A�m���ɑf���ł͂���܂���B
�����ŁA(i)��ے肷���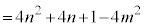 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA
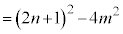 �ł����āA�A��(��)���l�����A
�ł����āA�A��(��)���l�����A m��0�ȏォ��n���������������@���(����)
�Ƃ��āA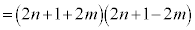 ��������
��������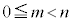 �ɂȂ����Ɖ��肷��ƁA
�ɂȂ����Ɖ��肷��ƁA 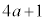 �ł���A
�ł���A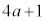 �C
�C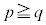 �͂��ꂼ��2�ȏ�̐����ł����āA
�͂��ꂼ��2�ȏ�̐����ł����āA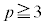 �͑f���ł͂���܂���B
�͑f���ł͂���܂���B
����ŁA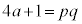 ��
�� 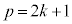 �������܂����B
�������܂����B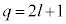 ��
�� 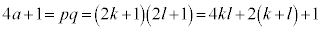 ���������̂ŁA���Ƃ́A
���������̂ŁA���Ƃ́A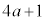 ��
�� 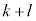 ��������A(i) �� (ii)�����������ƂɂȂ�܂��B(ii)��ے肵�Ă݂܂��B
��������A(i) �� (ii)�����������ƂɂȂ�܂��B(ii)��ے肵�Ă݂܂��B
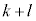 ���f���łȂ��Ɖ��肵�܂��B��̉ߒ����t�ɂ��ǂ�܂��Ba���������Ȃ̂ŁA
���f���łȂ��Ɖ��肵�܂��B��̉ߒ����t�ɂ��ǂ�܂��Ba���������Ȃ̂ŁA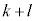 ��5�ȏ�̊�ł��B�f���łȂ�
��5�ȏ�̊�ł��B�f���łȂ�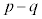 �́A1�����傫��2�̊p�Cq (
�́A1�����傫��2�̊p�Cq (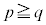 �C
�C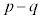 �Ƃ��܂�)�̐ς̌`
�Ƃ��܂�)�̐ς̌`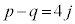 �@����C
�@����C�ɕ\����܂��Bp�Cq��0�ȏ�̐���k�Cl��p���āA
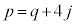 �C
�C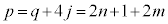 �@����D
�@����D�Ƃ����܂��B
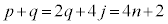 ��4�Ŋ����1�]�鐮���ł��B�E�ӂ�4�Ŋ�����1�]�鐔�ɂȂ�̂́A
��4�Ŋ����1�]�鐮���ł��B�E�ӂ�4�Ŋ�����1�]�鐔�ɂȂ�̂́A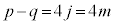 �������ɂȂ�ꍇ�ł��B
�������ɂȂ�ꍇ�ł��B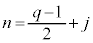 ����̂Ƃ��ɂ�4�Ŋ����3�]��܂�(��]�����Q��)�B
����̂Ƃ��ɂ�4�Ŋ����3�]��܂�(��]�����Q��)�B
 �������ɂȂ�Ƃ��Ak�Cl�̋���v��
�������ɂȂ�Ƃ��Ak�Cl�̋���v��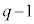 �͋����ł���A�D���A
�͋����ł���A�D���A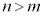 ��4�̔{��(
��4�̔{��(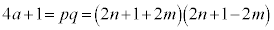 ���
���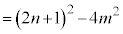 ��0�ȏ�)�ɂȂ�܂��B������j��0�ȏ�̐����Ƃ��āA
��0�ȏ�)�ɂȂ�܂��B������j��0�ȏ�̐����Ƃ��āA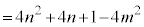 �C
�C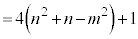 �Ƃ������Ƃ��ł��āA�B���Q�Ƃ��An�Cm��p���āA1�����傫���p�Cq���A
�Ƃ������Ƃ��ł��āA�B���Q�Ƃ��An�Cm��p���āA1�����傫���p�Cq���A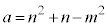 �C
�C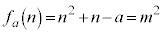 �@����E
�@����E�Ƃ������Ƃ���ƁA�����̘a�ƍ����Ƃ邱�Ƃɂ��A
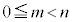 �C
�C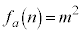
����āA
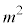 �C
�C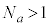
�����ɁAm��0�ȏ�̐����ł���A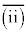 ��2�ȏ�̋����Ȃ̂�n�������ł����āA
��2�ȏ�̋����Ȃ̂�n�������ł����āA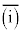 �ł��B(����)����������Ă��܂��B���̂Ƃ��A�C�C�E���A
�ł��B(����)����������Ă��܂��B���̂Ƃ��A�C�C�E���A ���A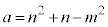 �ł���A
�ł���A �ƂȂ�A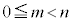 �ł����āA
�ł����āA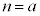 �̂Ƃ���
�̂Ƃ���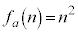 �ȊO�ɂ��A
�ȊO�ɂ��A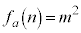 �ƂȂ镽����
�ƂȂ镽����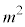 �����݂��܂��B�܂�A
�����݂��܂��B�܂�A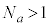 �ł��B
�ł��B
����ŁA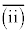 ��
�� 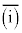 �������܂����B
�������܂����B 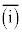 ��
�� 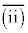 ���������̂ŁA(i) �� (ii)�������܂����B
���������̂ŁA(i) �� (ii)�������܂����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 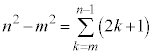 ���l�^�ɂ������ł��B�ȉ��̉͂������甭�z���Ă��܂��B
���l�^�ɂ������ł��B�ȉ��̉͂������甭�z���Ă��܂��B