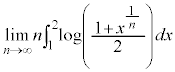東京大学理系2025年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 座標平面上の点A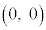 ,B
,B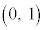 ,C
,C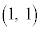 ,D
,D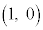 を考える。実数
を考える。実数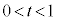 に対して、線分AB,BC,CDをt:
に対して、線分AB,BC,CDをt: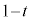 に内分する点をそれぞれ
に内分する点をそれぞれ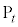 ,
,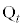 ,
,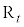 とし、線分
とし、線分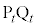 ,
,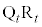 をt:
をt: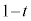 に内分する点をそれぞれ
に内分する点をそれぞれ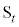 ,
,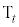 とする。さらに、線分
とする。さらに、線分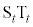 をt:
をt: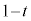 に内分する点を
に内分する点を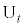 とする。また、点Aを
とする。また、点Aを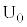 ,点Dを
,点Dを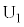 とする。
とする。
(1) 点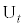 の座標を求めよ。
の座標を求めよ。
(2) t が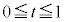 の範囲を動くときに点
の範囲を動くときに点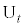 が描く曲線と、線分ADで囲まれた部分の面積を求めよ。
が描く曲線と、線分ADで囲まれた部分の面積を求めよ。
(3) aを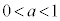 を満たす実数とする。t が
を満たす実数とする。t が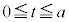 の範囲を動くときに点
の範囲を動くときに点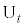 が描く曲線の長さを、aの多項式の形で求めよ。
が描く曲線の長さを、aの多項式の形で求めよ。 [解答へ]
[2](1) 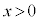 のとき、不等式
のとき、不等式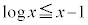 を示せ。
を示せ。
(2) 次の極限を求めよ。
[解答へ]
[3] 平行四辺形ABCDにおいて、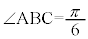 ,
,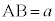 ,
,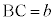 ,
,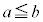 とする。次の条件を満たす長方形EFGHを考え、その面積をSとする。
とする。次の条件を満たす長方形EFGHを考え、その面積をSとする。
条件:点A,B,C,Dはそれぞれ辺EF,FG,GH,HE上にある。ただし、辺はその両端の点も含むものとする。
(1) 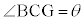 とするとき、Sをa,b,θを用いて表せ。
とするとき、Sをa,b,θを用いて表せ。
(2) Sのとりうる値の最大値をa,bを用いて表せ。
[解答へ]
[4] この問いでは、0以上の整数の2乗になる数を平方数と呼ぶ。aを正の整数とし、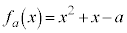 とおく。
とおく。
(1) nを正の整数とする。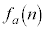 が平方数ならば、
が平方数ならば、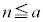 であることを示せ。
であることを示せ。
(2) 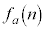 が平方数となる正の整数nの個数を
が平方数となる正の整数nの個数を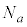 とおく。次の条件(i),(ii)が同値であることを示せ。
とおく。次の条件(i),(ii)が同値であることを示せ。 (i) 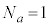 である。
である。 (ii) 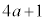 は素数である。
は素数である。 [解答へ]
[5] nを2以上の整数とする。1からnまでの数字が書かれた札が各1枚ずつ合計n枚あり、横一列におかれている。1以上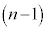 以下の整数i に対して、次の操作(
以下の整数i に対して、次の操作(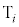 )を考える。
)を考える。
(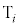 ) 左からi 番目の札の数字が、左から
) 左からi 番目の札の数字が、左から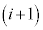 番目の札の数字よりも大きければ、これら2枚の札の位置を入れかえる。そうでなければ、札の位置を変えない。
番目の札の数字よりも大きければ、これら2枚の札の位置を入れかえる。そうでなければ、札の位置を変えない。 最初の位置において札は左から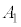 ,
,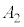 ,・・・,
,・・・,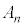 であったとする。この状態から
であったとする。この状態から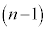 回の操作
回の操作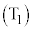 ,
,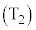 ,・・・,
,・・・,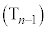 を順に行った後、続けて
を順に行った後、続けて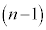 回の操作
回の操作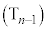 ,・・・,
,・・・,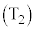 ,
,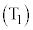 を順に行ったところ、札の数字は左から1,2,・・・,nと小さい順に並んだ。以下の問いに答えよ。
を順に行ったところ、札の数字は左から1,2,・・・,nと小さい順に並んだ。以下の問いに答えよ。
(1) 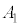 と
と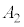 のうち少なくとも一方は2以下であることを示せ。
のうち少なくとも一方は2以下であることを示せ。
(2) 最初の状態としてありうる札の数字の並び方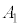 ,
,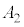 ,・・・,
,・・・,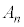 の総数を
の総数を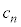 とする。nが4以上の整数であるとき、
とする。nが4以上の整数であるとき、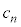 を
を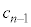 と
と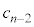 を用いて表せ。
を用いて表せ。 [解答へ]
[6] 複素数平面上の点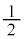 を中心とする半径
を中心とする半径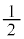 の円の周から原点を除いた曲線をCとする。
の円の周から原点を除いた曲線をCとする。
(1) 曲線C上の複素数zに対し、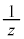 の実部は1であることを示せ。
の実部は1であることを示せ。
(2) α,βを曲線C上の相異なる複素数とするとき、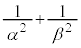 がとりうる範囲を複素数平面上に図示せよ。
がとりうる範囲を複素数平面上に図示せよ。
(3) γを(2)で求めた範囲に属さない複素数とするとき、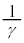 の実部がとりうる値の最大値と最小値を求めよ。
の実部がとりうる値の最大値と最小値を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。