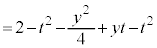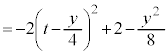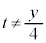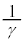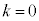���嗝�n���w'25�N�O��[6]
���f�����ʏ�̓_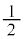 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a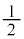 �̉~�̎����猴�_���������Ȑ���C�Ƃ���B
�̉~�̎����猴�_���������Ȑ���C�Ƃ���B
(1) �Ȑ�C��̕��f��z�ɑ��A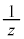 �̎�����1�ł��邱�Ƃ������B
�̎�����1�ł��邱�Ƃ������B
(2) α�Cβ���Ȑ�C��̑��قȂ镡�f���Ƃ���Ƃ��A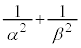 ���Ƃ肤��͈͂f�����ʏ�ɐ}������B
���Ƃ肤��͈͂f�����ʏ�ɐ}������B
(3) γ��(2)�ŋ��߂��͈͂ɑ����Ȃ����f���Ƃ���Ƃ��A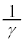 �̎������Ƃ肤��l�̍ő�l�ƍŏ��l�����߂�B
�̎������Ƃ肤��l�̍ő�l�ƍŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���f�����ʂ̖��ł́A���ʂ́A���f���̌`�̂܂܁A��Βl��Ίp���l��������v�Z�����N�Ȃ��Ƃ������̂ł����A�{��ł́u�����v�Ƃ������t���o�Ă���̂ŁA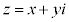 �Ƃ���x�Cy���l����������N���Ǝv���܂��B(2)�͓���ŕp�o��2�ϐ����ɂȂ�܂����A������Œ肵�đ��������A�Ƃ��ď�������̂��퓅��i�ł��B�����ł�y���W���Œ肵��x�͈̔͂��l���܂��B�Ȃ��A���f���̐}�`�I���p���Q�Ƃ��Ă��������B
�Ƃ���x�Cy���l����������N���Ǝv���܂��B(2)�͓���ŕp�o��2�ϐ����ɂȂ�܂����A������Œ肵�đ��������A�Ƃ��ď�������̂��퓅��i�ł��B�����ł�y���W���Œ肵��x�͈̔͂��l���܂��B�Ȃ��A���f���̐}�`�I���p���Q�Ƃ��Ă��������B
�Ȑ�C��̓_P��\�����f����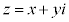 (x�Cy�͎����C
(x�Cy�͎����C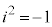 )�Ƃ���ƁA
)�Ƃ���ƁA
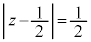 �@(
�@(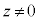 )�@����@
)�@����@
(1) 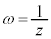 �Ƃ����ƁA
�Ƃ����ƁA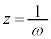
�@�ɑ�����āA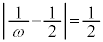 ���A
���A 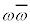 �������āA
�������āA����āAω�̎����́A
�ʉ��D�@���A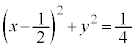 �@(
�@(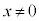 )�@����A
)�@����A 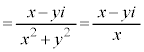 �@(�� �B)
�@(�� �B)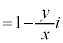
������A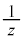 �̎�����1�ł��B
�̎�����1�ł��B
(2) (1)�ʉ��ɂ��ƁA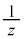 �̋���
�̋���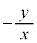 �́A���_�Ɖ~�A��̓_
�́A���_�Ɖ~�A��̓_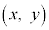 �����Ԓ����̌X���̕�����ς������̂Ȃ̂ŁA���炩�ɑS��������蓾�܂��B�����ŁA������1�ł��镡�f��
�����Ԓ����̌X���̕�����ς������̂Ȃ̂ŁA���炩�ɑS��������蓾�܂��B�����ŁA������1�ł��镡�f��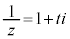 ���At ��C�ӂ̎����Ƃ��āA
���At ��C�ӂ̎����Ƃ��āA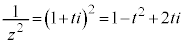 �Ƃ������Ƃ��ł��܂��B
�Ƃ������Ƃ��ł��܂��B 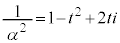 �@����C
�@����C�C���A�~C��̓_��\�����f����α�Ƃ��āA
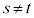 �@����D
�@����D�Ƃ������Ƃ��ł��܂��Bα�ƈقȂ�A�~C��̓_��\�����f����β�Cs��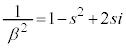 �ƂȂ�C�ӂ̎����Ƃ��āA�D�Ɠ��l�ɁA
�ƂȂ�C�ӂ̎����Ƃ��āA�D�Ɠ��l�ɁA 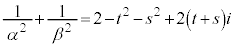 �@����E
�@����E�Ƃ������Ƃ��ł��܂��B�D�{�E���A
�����ŁA�V���ɁA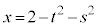 �̎�����x�C������y�ƕ\���ƁA
�̎�����x�C������y�ƕ\���ƁA 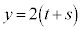 �C
�C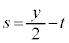
�������s����������ƁA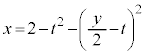 ���A
���A �����ŁAy���Œ肵�čl���Ax��C�ӂ̎���t�̊��ƍl���܂��B�A���A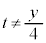 ���A
���A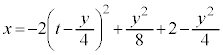 �ł��B
�ł��B 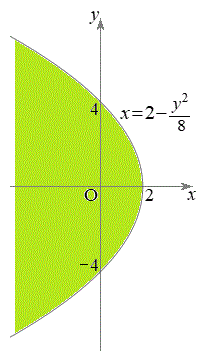 t ��
t ��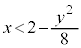 �����������Ƃ�Ƃ��Ax�́A
�����������Ƃ�Ƃ��Ax�́A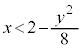 �����܂�(2�����̍ő�ŏ����Q��)�B
�����܂�(2�����̍ő�ŏ����Q��)�B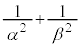 ��
��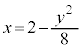 �̂Ƃ肤��͈͂�^���܂��B������
�̂Ƃ肤��͈͂�^���܂��B������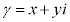 �̍����̕����ł��B�}������ƉE�}���ΐF���F��(���E������܂܂Ȃ�)�B
�̍����̕����ł��B�}������ƉE�}���ΐF���F��(���E������܂܂Ȃ�)�B
(3) (2)�ŋ��߂��͈͂ɑ����Ȃ����f����γ�Ƃ���̂ŁA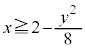 (x�Cy�͎���)�Ƃ���ƁAx�Cy�́A
(x�Cy�͎���)�Ƃ���ƁAx�Cy�́A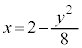 �����܂��B���̗̈�D�́A������
�����܂��B���̗̈�D�́A������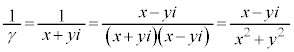 ����E���̗̈�ł��B
����E���̗̈�ł��B 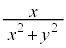 �̎�����
�̎�����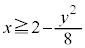 �ł��B
�ł��B
�̈�D�F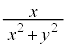 ���̊e�_�ɂ���
���̊e�_�ɂ���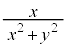 �̒l���v�Z����̂ł͑�ςȂ̂ŁA�v�̂悭�������邱�Ƃ��l���܂��B
�̒l���v�Z����̂ł͑�ςȂ̂ŁA�v�̂悭�������邱�Ƃ��l���܂��B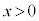 ��
��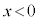 �̂Ƃ��͐��A
�̂Ƃ��͐��A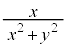 �̂Ƃ��͕��̒l���Ƃ�܂��B�ő�l���Ƃ�Ƃ���ΐ��̒l�A�ŏ��l���Ƃ�Ƃ���Ε��̒l�ł��B�܂�A
�̂Ƃ��͕��̒l���Ƃ�܂��B�ő�l���Ƃ�Ƃ���ΐ��̒l�A�ŏ��l���Ƃ�Ƃ���Ε��̒l�ł��B�܂�A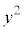 �̐�Βl�͂������ꂽ�͈͂̒l���Ƃ�̂��낤�A�Ɛ��@�ł��܂��B�Ƃ���ƁA�����
�̐�Βl�͂������ꂽ�͈͂̒l���Ƃ�̂��낤�A�Ɛ��@�ł��܂��B�Ƃ���ƁA�����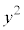 �ɒ��ڂł��܂��B
�ɒ��ڂł��܂��B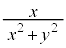 ���������Ȃ��
���������Ȃ��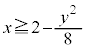 �̐�Βl�͑傫���Ȃ�܂��BD�F
�̐�Βl�͑傫���Ȃ�܂��BD�F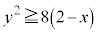 ��ό`����ƁA
��ό`����ƁA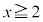 �ƂȂ�܂����A
�ƂȂ�܂����A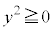 �ɂ����Ă�
�ɂ����Ă�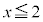 �ł���
�ł���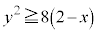 �͕��ɂȂ�Ȃ��̂�
�͕��ɂȂ�Ȃ��̂�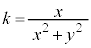 �C
�C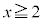 �ɂ����Ă�
�ɂ����Ă�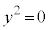 �ł�(
�ł�(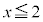 )�B
)�B
�܂�A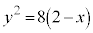 �́A
�́A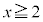 �ɂ����Ă�
�ɂ����Ă�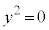 �̂Ƃ��ɍő�l�A�ŏ��l���Ƃ�A
�̂Ƃ��ɍő�l�A�ŏ��l���Ƃ�A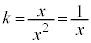 �ɂ����Ă�
�ɂ����Ă�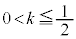 �̂Ƃ��ɍő�l�E�ŏ��l���Ƃ�܂��B
�̂Ƃ��ɍő�l�E�ŏ��l���Ƃ�܂��B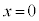 �̂Ƃ��A
�̂Ƃ��A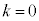
������āA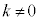 �C
�C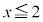 �@����G
�@����G
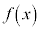 �̂Ƃ���
�̂Ƃ���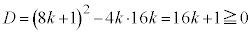 �ƂȂ�܂����A
�ƂȂ�܂����A
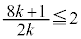 �̂Ƃ��Ax��2���������G�́A
�̂Ƃ��Ax��2���������G�́A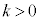 �͈̔͂Ɏ������������܂��B�G�̍��ӂ�
�͈̔͂Ɏ������������܂��B�G�̍��ӂ�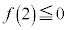 �Ƃ����ƁA���̏���(2���������̈�ʘ_���Q��)�́A
�Ƃ����ƁA���̏���(2���������̈�ʘ_���Q��)�́A ���ʎ�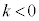 �@����G
�@����G
���F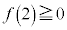 �@����H
�@����H
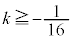 ����
����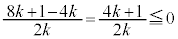 �@����I
�@����I
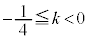 ����
����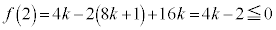 �@����J
�@����J �Ƃ��āA�u�G���H�v�܂��͇I�܂��͇J�ł��B
�G���A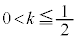
�H���A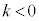 �C
�C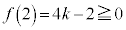
�I���A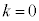 ����
����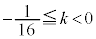 �C
�C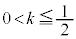
�J���A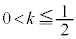 ����
����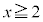 �C�������k�͂���܂���B
�C�������k�͂���܂���B
����āA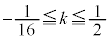 �܂���
�܂���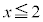 �܂���
�܂���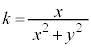 �@����K
�@����K �F�F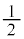 (
(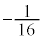 )�C�K�F
)�C�K�F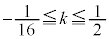 (
(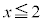 )���A
)���A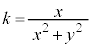 �̍ő�l��
�̍ő�l��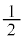 �C�ŏ��l��
�C�ŏ��l��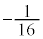 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2026(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 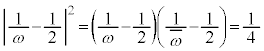
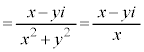 �@(�� �B)
�@(�� �B)