���嗝�n���w'25�N�O��[3]
���s�l�ӌ`ABCD�ɂ����āA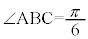 �C
�C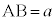 �C
�C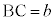 �C
�C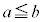 �Ƃ���B���̏������������`EFGH���l���A���̖ʐς�S�Ƃ���B
�Ƃ���B���̏������������`EFGH���l���A���̖ʐς�S�Ƃ���B
�����F�_A�CB�CC�CD�͂��ꂼ���EF�CFG�CGH�CHE��ɂ���B�������A�ӂ͂��̗��[�̓_���܂ނ��̂Ƃ���B
(1) 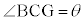 �Ƃ���Ƃ��AS��a�Cb�Cθ��p���ĕ\���B
�Ƃ���Ƃ��AS��a�Cb�Cθ��p���ĕ\���B
(2) S�̂Ƃ肤��l�̍ő�l��a�Cb��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@������������ɍő�l�����߂�ꂻ���ł����A�����̒l��1�ɂȂ蓾�邩�ǂ����A�Ƃ������Ƃ��{��ł͊ȒP�Șb�ł͂���܂���B�܂��A�ȉ��̉ł�a�Cb��2�ϐ������o�Ă��܂��B����ł́A2�ϐ����͕p�o�e�[�}�ł��B2�ϐ��̂����Е����Œ肵�Ă����āA���������čő�ŏ����l���A����ɌŒ肵�Ă������������A�Ƃ�����@���Ƃ邱�Ƃ������̂ł����A�ȉ��ł́Aa�Cb�̓�����(a�ɂ��Ă�b�ɂ��Ă�2����)�ł�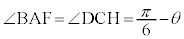 �ȂǂƂ�����t ��1�ϐ����Ƃ��Ĉ�����A�Ƃ����Z�I��p���ĉ��Ă��܂��B
�ȂǂƂ�����t ��1�ϐ����Ƃ��Ĉ�����A�Ƃ����Z�I��p���ĉ��Ă��܂��B
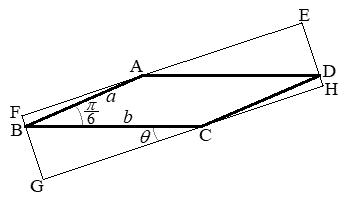 �E�}���A
�E�}���A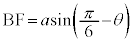 �C
�C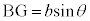 �C
�C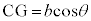 �C
�C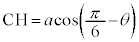 �C
�C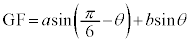
����āA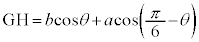 �C
�C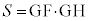
(1) 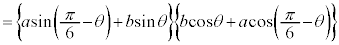
(2) 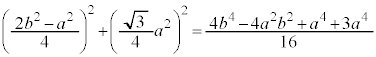 �@(�O�p���̍������Q��)
�@(�O�p���̍������Q��)
���A
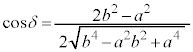 �@����@
�@����@������δ �́A�ȉ������p�B
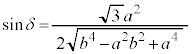 �C
�C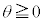 �@����A
�@����A�����ŁA��蕶�̏������A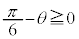 �C
�C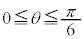 �C�܂�A
�C�܂�A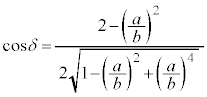 �@����B
�@����B
�A���A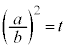 �@����C
�@����C
�ł����A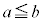 �@����D
�@����D
�Ƃ����ƁA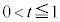 �ł����āA
�ł����āA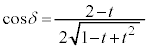 ���
���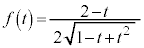 �ł��B
�ł��B �����ŁA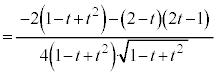 �@����E
�@����E
�Ƃ����ƁA ���A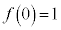 �́A
�́A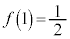 �ɂ�����t ���P���������ŁA
�ɂ�����t ���P���������ŁA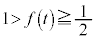 �C
�C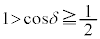 ���
���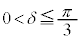 �C�܂�
�C�܂�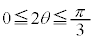 �@��
�@�� 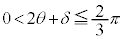 �@����F
�@����F
�B���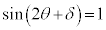 �C
�C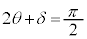 �@����G
�@����G
�@������ƁA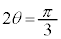 �C�܂�A
�C�܂�A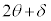 �̂Ƃ��ɍő�ɂȂ肻���Ȃ̂ł����Aδ���������Ƃ��ɁA
�̂Ƃ��ɍő�ɂȂ肻���Ȃ̂ł����Aδ���������Ƃ��ɁA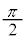 �ɂȂ����Ƃ��Ă��A
�ɂȂ����Ƃ��Ă��A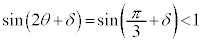 ��
��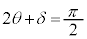 �����������A�B�͈̔͂̂��ׂĂ�θ�ɂ��āA
�����������A�B�͈̔͂̂��ׂĂ�θ�ɂ��āA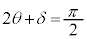 �ƂȂ邱�Ƃ����蓾�܂��B�G�͈̔͂̒���
�ƂȂ邱�Ƃ����蓾�܂��B�G�͈̔͂̒���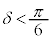 ���܂܂��̂ł����A�G�́A
���܂܂��̂ł����A�G�́A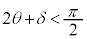 �ɂȂ�ꍇ���K������A�ƌ����Ă���킯�ł͂���܂���B
�ɂȂ�ꍇ���K������A�ƌ����Ă���킯�ł͂���܂���B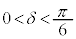 �̂Ƃ��Aθ���B�����ǂ�Ȓl���Ƃ��Ă��A
�̂Ƃ��Aθ���B�����ǂ�Ȓl���Ƃ��Ă��A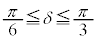 �ł��B�����ŇF���A
�ł��B�����ŇF���A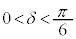 �̂Ƃ��ƁA
�̂Ƃ��ƁA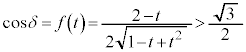 �̂Ƃ��ɕ����čl���܂��B
�̂Ƃ��ɕ����čl���܂��B �E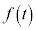 �̂Ƃ��A
�̂Ƃ��A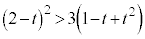 (
(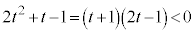 �͒P�������ł�)���A
�͒P�������ł�)���A �D���A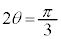 �C�܂�A
�C�܂�A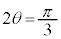 �@����H
�@����H
���̂Ƃ��́A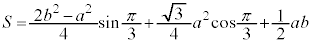 �ł���A�C���a�Cb���^������δ�͒萔�ł���A���̂Ƃ��@��θ�̑������Ȃ̂ŁA
�ł���A�C���a�Cb���^������δ�͒萔�ł���A���̂Ƃ��@��θ�̑������Ȃ̂ŁA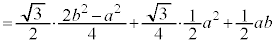 �̂Ƃ�S�ő�ƂȂ�܂��B(1)�̌��ʂ�
�̂Ƃ�S�ő�ƂȂ�܂��B(1)�̌��ʂ�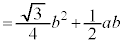 �Ƃ��āA
�Ƃ��āA 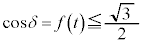
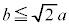 �@����I
�@����I���̂Ƃ��́A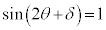 �C
�C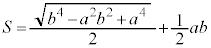 �̂Ƃ��A
�̂Ƃ��A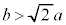 �C����
�C����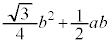 �ƂȂ蓾�܂��B����āA
�ƂȂ蓾�܂��B����āA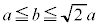 �̂Ƃ�S�ő�ƂȂ�܂��B�@��
�̂Ƃ�S�ő�ƂȂ�܂��B�@��
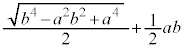 �Ƃ��āA
�Ƃ��āA 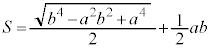 �@����K
�@����K�H�C�I�C�J�C�K���AS�̂Ƃ肤��l�̍ő�l�́A
�E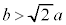 �̂Ƃ�
�̂Ƃ�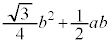
�E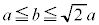 �̂Ƃ�
�̂Ƃ�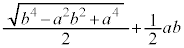 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 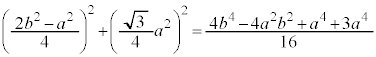 �@(�O�p���̍������Q��)
�@(�O�p���̍������Q��)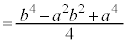
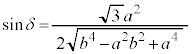 �C
�C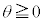 �@����A
�@����A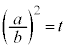 �@����C
�@����C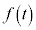
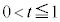
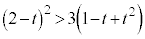 (
(