���嗝�n���w'97�N�O��[2]
n�𐳂̐����Aa�������Ƃ���B���ׂĂ̐���m�ɑ��āA
�����藧�悤��a�͈̔͂�n��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ݒ肪���G�ȓ��ł��B���͂��ׂăp�X���č\��Ȃ��A�ƁA�����Ȃ��Ƃ����������搶�����܂����A�ǂ̖������Ɍ����Ă��܂��Ƃ��ɂ́A������邵������܂���B�ǂ�����āA�A�v���[�`���čs�����l���Ă݂܂��傤�B
���̖�肪�ǂ����ē��ɂȂ��Ă��܂����A�ƌ����ƁAn�����̐����Ƃ��������ŋ�̓I�Ȓl���^�����Ă��Ȃ����ƂƁAm���u���ׂĂ̎����v�ł͂Ȃ��u���ׂĂ̐����v�ɂȂ��Ă��邱�Ƃɂ���܂��B
�����ŁA�܂��A���̌��ȏ����ݒ����߁A���������ȒP�ɂȂ�悤�ɁAn�ɋ�̓I�Ȑ������A����m�ł͂Ȃ��A����x�Ƃ��ĕs�������l���Ă݂܂��B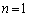 �Ƃ���ƁA
�Ƃ���ƁA
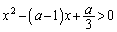 �@����@
�@����@
���ӂ�x�̊��Ƃ݂ĕ�����������̂ł����(2�������Q��)�A
�� 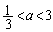
�Ƃ������ƂɂȂ�܂��B
�{��ɖ߂��āA�����悤�ɁA
���ׂĂ̎���x�ɂ���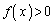 �ƂȂ�����́A�E�ӂ̑�2��(
�ƂȂ�����́A�E�ӂ̑�2��(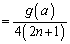 �Ƃ����܂�)�����ƂȂ邱�Ƃł��B
�Ƃ����܂�)�����ƂȂ邱�Ƃł��B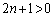 �Ȃ̂ŁA
�Ȃ̂ŁA
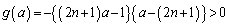 �@����A
�@����A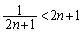 ���A
���A
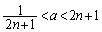 �@����B
�@����B
�ł����A���߂�����́A�u���ׂĂ̎���x�ɂ��āv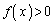 �ƂȂ邱�Ƃł͂Ȃ��A�u���ׂĂ̐���m�ɂ��āv
�ƂȂ邱�Ƃł͂Ȃ��A�u���ׂĂ̐���m�ɂ��āv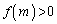 �ƂȂ邱�Ƃł��B
�ƂȂ邱�Ƃł��B
�A�̏������l�����̂́A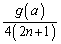 ��
��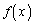 �̍ŏ��l������ł��B
�̍ŏ��l������ł��B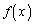 ���ŏ��l���Ƃ�̂́A
���ŏ��l���Ƃ�̂́A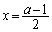 �̂Ƃ��ł��Bm�𐮐��Ƃ���
�̂Ƃ��ł��Bm�𐮐��Ƃ���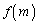 �̍ŏ��l���l����ꍇ�ɂ́A
�̍ŏ��l���l����ꍇ�ɂ́A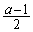 �͐����Ƃ͌���Ȃ��̂ŁA
�͐����Ƃ͌���Ȃ��̂ŁA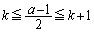 ��������k�ɑ��āA
��������k�ɑ��āA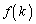 ��
��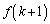 �̂����̏����������ŏ��l�Ƃ��Ȃ�������܂���B
�̂����̏����������ŏ��l�Ƃ��Ȃ�������܂���B
�Ƃ���ŁA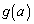 �͇A�̏������ŁAa���B�͈̔͂̏���Ɖ����̒l�ɋ߂Â��Ƃ��Ɏ���ɏ������Ȃ�܂��B
�͇A�̏������ŁAa���B�͈̔͂̏���Ɖ����̒l�ɋ߂Â��Ƃ��Ɏ���ɏ������Ȃ�܂��B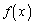 �̍ŏ��l���l����̂�
�̍ŏ��l���l����̂�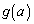 ���ŏ��ɂȂ�Ƃ���A�B�͈̔͂̏���Ɖ����ɂ�����
���ŏ��ɂȂ�Ƃ���A�B�͈̔͂̏���Ɖ����ɂ�����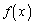 �̍ŏ��ׂĂ݂܂��B
�̍ŏ��ׂĂ݂܂��B
�E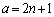 �̂Ƃ��A
�̂Ƃ��A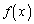 ���ŏ��Ƃ���x�̒l�́A
���ŏ��Ƃ���x�̒l�́A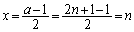 (����)�ł����āA�ŏ��l
(����)�ł����āA�ŏ��l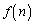 �ɂ��āA
�ɂ��āA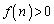 �Ƃ���A
�Ƃ���A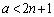 �@����C�@�Ƃ����������o�Ă��܂��B
�@����C�@�Ƃ����������o�Ă��܂��B �E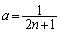 �̂Ƃ���
�̂Ƃ���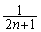 �͐����ł͂���܂���B
�͐����ł͂���܂���B 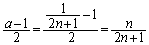 �C
�C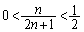
���A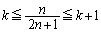 ��������k��
��������k��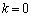 �ł��B
�ł��B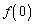 ��
��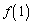 �̑召���r����ƁA
�̑召���r����ƁA 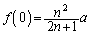 �C
�C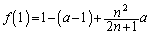
���A
�]���āA�ŏ��l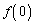 �ɂ��āA
�ɂ��āA �� 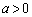 �@����D
�@����D �C�C�D���A
�ƂȂ�܂��B
�������Ŏ���I�ɂ͒��ԓ_�_���̏�L���炢�ŏ[�����Ǝv���܂����A�����t��̊��͖Ƃ�Ȃ��̂ŁA���i�������̂ł���A�ȉ��̂悤�ɂ��܂��B
�@�̕s�������l�����ŁA������L���Ȏ�i������܂��B�萔�̕����Ƃ����Z�I�ł��B�K����������Ƃ����ۏ͂���܂��A�{��ł͗L���ł��B
�@�ł���A
�Ȃǂƕό`���āA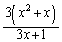 ���Ƃ蓾��l�͈̔͂��l����̂ł��B
���Ƃ蓾��l�͈̔͂��l����̂ł��B
n�𐳂̐����Aa�������Ƃ��āA���ׂĂ̐���m�ɑ��āA
�ƂȂ�̂ł���A
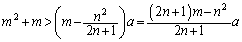 �@����E
�@����E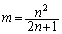 (
(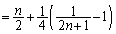 �͐����łȂ�)�ƂȂ蓾�Ȃ��̂ŁA(i)
�͐����łȂ�)�ƂȂ蓾�Ȃ��̂ŁA(i) 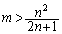 �C(ii)
�C(ii) 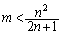 �C�Əꍇ�������܂��B
�C�Əꍇ�������܂��B
(i) 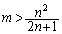 �̂Ƃ��A
�̂Ƃ��A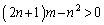 �Ȃ̂ŁA
�Ȃ̂ŁA �E �� 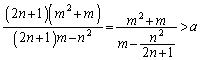 �@����F
�@����F 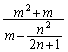 �̂Ƃ蓾��l�ׂ邽�߂ɁA��
�̂Ƃ蓾��l�ׂ邽�߂ɁA��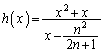 ���l���܂��B
���l���܂��B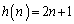 �C
�C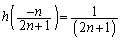
�܂��A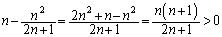 ���A
���A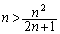 �����\���(���̑������Q��)�A
�����\���(���̑������Q��)�A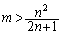 �̂Ƃ��A
�̂Ƃ��A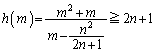 (����������
(����������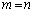 �̂Ƃ�)����āA�F�����藧���߂ɁA
�̂Ƃ�)����āA�F�����藧���߂ɁA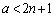 �@����G
�@����G (ii) 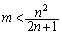 �̂Ƃ��A
�̂Ƃ��A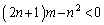 �Ȃ̂ŁA
�Ȃ̂ŁA �E �� 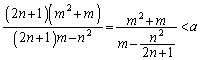 �@����H
�@����H (i)��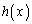 �̑����\�𗘗p����ƁA
�̑����\�𗘗p����ƁA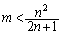 �̂Ƃ��A
�̂Ƃ��A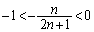 ��
��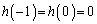 ���A
���A 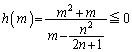 (����������
(����������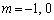 �̂Ƃ�)
�̂Ƃ�)����āA�H���������邽�߂ɁA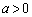 �@����I
�@����I �G�C�I���A
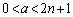 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 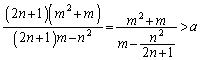 �@����F
�@����F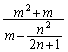 �̂Ƃ蓾��l�ׂ邽�߂ɁA��
�̂Ƃ蓾��l�ׂ邽�߂ɁA��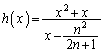 ���l���܂��B
���l���܂��B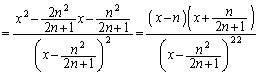
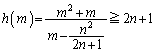 (����������
(����������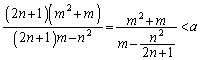 �@����H
�@����H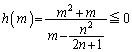 (����������
(����������