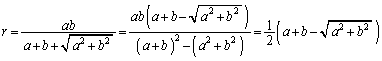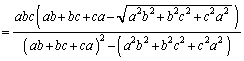���嗝�H���w'05�N[1]
4�_O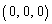 �CA
�CA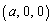 �CB
�CB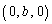 �CC
�CC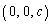 �_�Ƃ���l�ʑ̂��l����B�������A
�_�Ƃ���l�ʑ̂��l����B�������A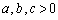 �Ƃ���B�ȉ��̖�ɓ�����B
�Ƃ���B�ȉ��̖�ɓ�����B
(1) 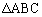 �̖ʐς����߂�B
�̖ʐς����߂�B (2) 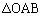 �̓��ډ~�̒��S�̍��W�����߂�B
�̓��ډ~�̒��S�̍��W�����߂�B (3) �l�ʑ�OABC�̊e�ʂɐڂ��鋅�̒��S�̍��W�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
����āA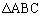 �̖ʐ�S�́A
�̖ʐ�S�́A 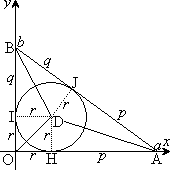
(2) 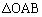 �ɓ��ڂ���~�́AOA�COB�CAB��3�ӂɐڂ���̂ŁA���߂�~�̒��S��D�C���a��r�Ƃ���ƁAD��OA�COB�CAB�Ƃ̋����͂������r�ł��BD�̍��W��
�ɓ��ڂ���~�́AOA�COB�CAB��3�ӂɐڂ���̂ŁA���߂�~�̒��S��D�C���a��r�Ƃ���ƁAD��OA�COB�CAB�Ƃ̋����͂������r�ł��BD�̍��W��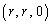 �ł��B���̂Ƃ��A
�ł��B���̂Ƃ��A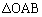 �̖ʐς�
�̖ʐς�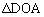 �C
�C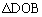 �C
�C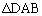 �̖ʐς̘a�ł��B
�̖ʐς̘a�ł��B 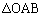 �̖ʐς�
�̖ʐς�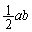
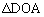 �C
�C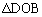 �C
�C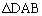 �̖ʐς́A���ꂼ��A
�̖ʐς́A���ꂼ��A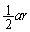 �C
�C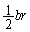 �C
�C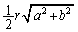 �C����āA
�C����āA�� 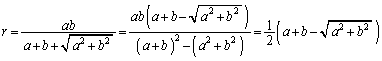 �~�̒��S�̍��W�́A
�~�̒��S�̍��W�́A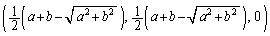 ......[��]
......[��]
[�ʉ�]�@D����OA�COB�CAB�ɉ��낵�������̑����AH�CI�CJ�Ƃ���ƁA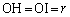 �ł��B
�ł��B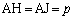 �C
�C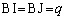 �Ƃ����ƁA
�Ƃ����ƁA �@�{�A�����A�B��������ƁA
�� 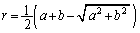
(3) �l�ʑ�OABC�̊e�ʂɐڂ��鋅�́Ayz���ʁCzx���ʁCxy���ʂ̂�����Ƃ��ڂ���̂ŁA���̒��S��E�C���a��r�Ƃ���ƁAE��yz���ʁCzx���ʁCxy���ʂƂ̋����͂������r�ł��BE�̍��W��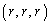 �ł��B���̂Ƃ��A�l�ʑ�OABC�̑̐ς̘a�́A�l�ʑ�EOAB�C�l�ʑ�EOBC�C�l�ʑ�EOAC�C�l�ʑ�EABC�̑̐ς̘a�ł��B
�ł��B���̂Ƃ��A�l�ʑ�OABC�̑̐ς̘a�́A�l�ʑ�EOAB�C�l�ʑ�EOBC�C�l�ʑ�EOAC�C�l�ʑ�EABC�̑̐ς̘a�ł��B �l�ʑ�OABC�̑̐ς́A��ʂ�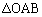 �̖ʐς�
�̖ʐς�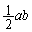 �C����c�̎O�p���̑̐ςŁA
�C����c�̎O�p���̑̐ςŁA �l�ʑ�EOAB�̑̐ς́A��ʂ�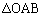 �̖ʐς�
�̖ʐς�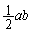 �C����r�̎O�p���̑̐ςŁA
�C����r�̎O�p���̑̐ςŁA �l�ʑ�EOBC�̑̐ς́A��ʂ�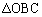 �̖ʐς�
�̖ʐς�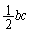 �C����r�̎O�p���̑̐ςŁA
�C����r�̎O�p���̑̐ςŁA �l�ʑ�EOAC�̑̐ς́A��ʂ�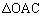 �̖ʐς�
�̖ʐς�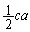 �C����r�̎O�p���̑̐ςŁA
�C����r�̎O�p���̑̐ςŁA �l�ʑ�EABC�̑̐ς́A��ʂ�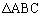 �̖ʐς�(1)���
�̖ʐς�(1)���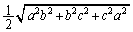 �C����r�̎O�p���̑̐ςŁA
�C����r�̎O�p���̑̐ςŁA ����āA
�� 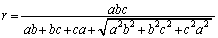
���̒��S�̍��W�́A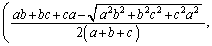
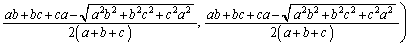 ......[��]
......[��]
(2)�����̂悤�ɍl���邱�Ƃ��ł��܂��B
xy���ʏ�ɂ����āA2�_A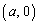 �CB
�CB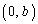 ��ʂ钼���́A
��ʂ钼���́A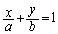 �ƕ\���܂��Bab�������āA
�ƕ\���܂��Bab�������āA 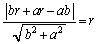 ����C
����C�C�̐�Βl�L���̓����͕��ł��B�Ȃ��Ȃ�A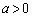 �C
�C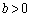 �Ȃ̂ŁA�_
�Ȃ̂ŁA�_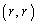 �ƌ��_�͂Ƃ��ɁA����AB�̉����ɂ����āA�������ɂ��邩��ł��B����āA
�ƌ��_�͂Ƃ��ɁA����AB�̉����ɂ����āA�������ɂ��邩��ł��B����āA �� 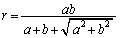
���l�ɂ���(3)�����̂悤�ɍl���邱�Ƃ��ł��܂��B
xyz��Ԃɂ����āA3�_A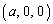 �CB
�CB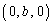 �CC
�CC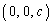 ��ʉ߂��镽��π�́A
��ʉ߂��镽��π�́A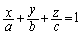 �ƕ\���܂��Babc�������āA
�ƕ\���܂��Babc�������āA 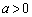 �C
�C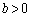 �C
�C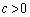 �Ȃ̂ŁA�_
�Ȃ̂ŁA�_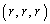 �ƌ��_������π�Ɋւ��ē������ɂ��邱�Ƃ��l����ƁA��Βl�L�����͕��ł��B����āA
�ƌ��_������π�Ɋւ��ē������ɂ��邱�Ƃ��l����ƁA��Βl�L�����͕��ł��B����āA�� 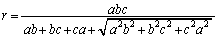
�NjL�F(2)��(3)�͔��a���������낤�ɂˁI��1�s�ɓ��肫��Ȃ��̂Ō���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B