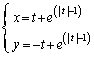早稲田大学理工学部2005年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 4点O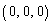 ,A
,A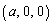 ,B
,B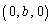 ,C
,C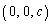 を頂点とする四面体を考える。ただし、
を頂点とする四面体を考える。ただし、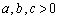 とする。以下の問に答えよ。
とする。以下の問に答えよ。
(1) 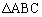 の面積を求めよ。
の面積を求めよ。 (2) 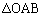 の内接円の中心の座標を求めよ。
の内接円の中心の座標を求めよ。 (3) 四面体OABCの各面に接する球の中心の座標を求めよ。
[解答へ]
[2] 円周上にm個の点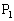 ,
,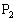 ,・・・,
,・・・,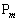 がこの順に配置され、各点
がこの順に配置され、各点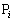 に一つの実数
に一つの実数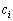 が与えられている(
が与えられている(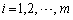 )。ただし、
)。ただし、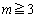 とする。さらに、
とする。さらに、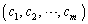 は条件
は条件
(*) 各点の値は、隣接する2点の値の和に等しい
を満たす。このとき、以下の問に答えよ。
(1) 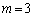 のとき、
のとき、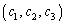 の値を求めよ。
の値を求めよ。 (2) 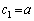 ,
,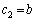 とおくとき、
とおくとき、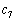 をa,bで表せ。ただし、
をa,bで表せ。ただし、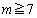 とする。
とする。 (3) 条件(*)をみたし、かつ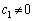 となる
となる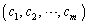 が存在するのはmがどのような自然数のときか。mが満たすべき必要十分条件を求め、その理由を簡単に述べよ。
が存在するのはmがどのような自然数のときか。mが満たすべき必要十分条件を求め、その理由を簡単に述べよ。 [解答へ]
[3] 袋の中に1からnまでの番号のついたn個の玉が入っている。この袋から玉を1個取り出し、番号を調べてもとに戻すことをr回行うとき、取り出された玉の番号の最大値をXとする。以下の問に答えよ。
(1) 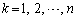 に対して、Xがちょうどkとなる確率を求めよ。
に対して、Xがちょうどkとなる確率を求めよ。 (2) 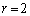 のとき、Xの期待値を求めよ。
のとき、Xの期待値を求めよ。 (3) 一般のrに対してXの期待値を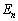 とおくとき、極限値
とおくとき、極限値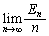 を求めよ。
を求めよ。 [解答へ]
[4] 複素数zが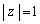 を満たしながら動くとき、次の式で定まるwについて以下の問に答えよ。
を満たしながら動くとき、次の式で定まるwについて以下の問に答えよ。
(1) wの虚部の取る値の範囲を求めよ。
(2) wが複素数平面上に描く曲線の長さを求めよ。(複素数平面上の長さは座標平面上の長さと同じとする。)
[解答へ]
[5] 媒介変数tにより
と表されるxy平面上の曲線Cについて以下の問に答えよ。
(1) 曲線Cと座標軸が接する点の座標を求めよ。
(2) 曲線Cとx軸,y軸で囲まれた部分をx軸のまわりに1回転させてできる立体の体積を求めよ。
(3) (2)で求めた体積をVとするとき、V,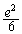 ,
,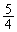 を小さい順に並べよ。ただし、
を小さい順に並べよ。ただし、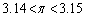 および
および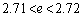 は既知とする。
は既知とする。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。