早大理工数学'05年[3]
袋の中に1からnまでの番号のついたn個の玉が入っている。この袋から玉を1個取り出し、番号を調べてもとに戻すことをr回行うとき、取り出された玉の番号の最大値をXとする。以下の問に答えよ。
(1) 
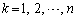に対して、Xがちょうどkとなる確率を求めよ。 (2) 
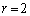のとき、Xの期待値を求めよ。 (3) 一般のrに対してXの期待値を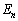
とおくとき、極限値
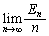を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (1) r回試行を行って、最大値がkになるということは、r回すべて玉の番号が1〜kのどれかであって、かつ、「r回すべて玉の番号が1〜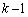
のどれか」ではない(つまり、r回のうち少なくとも1回はkが出ている)、ということです。 r回すべて玉の番号が1〜kのどれかになる確率は、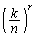
です(独立試行の確率を参照)。r回すべて玉の番号が1〜
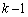のどれかになる確率は、
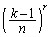です。
∴ 
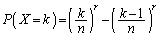......[答]
(3) rが任意の自然数のとき、
ここで、
より、
従って、
この右辺は、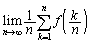
に近い形をしているので、区分求積法にするのだろうと思うのですが、中カッコの中では、kと
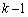が混在しているので、このままでは、区分求積法に持ち込むことができません。
そこでkだけ、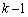
だけ、という形をひねり出すために、はさみうちの原理を使います。jを
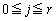をみたす整数だとして、
(
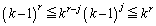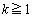)より、 ∴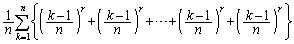 
左辺の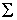
は、kを1からnまで動かすときに、
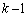が0から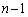
まで変わるので、
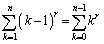という具合に直せば、
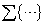の中の中カッコ内は、r項の和になっているので、 ここで、左辺、右辺ともに、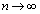
のとき、 よって、はさみうちの原理より、
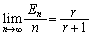......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
......[答]
