���嗝�H���w'05�N[4]
���f��z��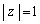 �����Ȃ��瓮���Ƃ��A���̎��Œ�܂�w�ɂ��Ĉȉ��̖�ɓ�����B
�����Ȃ��瓮���Ƃ��A���̎��Œ�܂�w�ɂ��Ĉȉ��̖�ɓ�����B
(1) w�̋����̎��l�͈̔͂����߂�B
(2) w�����f�����ʏ�ɕ`���Ȑ��̒��������߂�B(���f�����ʏ�̒����͍��W���ʏ�̒����Ɠ����Ƃ���B)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�͌��s�ے��ł͔͈͊O�̖��ł��B
(1) 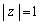 ���݂������f���́A
���݂������f���́A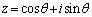 (
(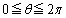 )�ƕ\���܂��B
)�ƕ\���܂��B 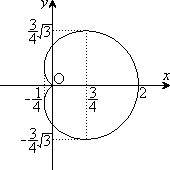
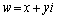 (x�Cy�͎���)�Ƃ����ƁA
(x�Cy�͎���)�Ƃ����ƁA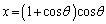 �C
�C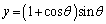 ����@
����@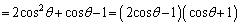 ����A
����A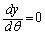 �Ƃ���ƁA
�Ƃ���ƁA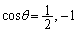
�� 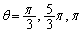
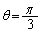 �̂Ƃ��A
�̂Ƃ��A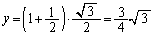 �C
�C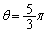 �̂Ƃ��A
�̂Ƃ��A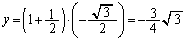 �����\���Aw�̋���y�̂Ƃ�͈͂�(���̑������Q��)�A
�����\���Aw�̋���y�̂Ƃ�͈͂�(���̑������Q��)�A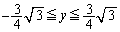 ......[��]
......[��]
(2) 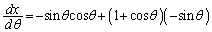
�� 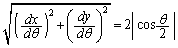
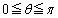 �ɂ�����
�ɂ�����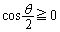 �C
�C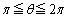 �ɂ�����
�ɂ�����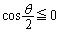
���߂��Ȑ��̒����́A(1)��y�̕ω��̂��������A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B