���嗝�H���w'05�N[5]
�}��ϐ�t�ɂ��
�ƕ\�����xy���ʏ�̋Ȑ�C�ɂ��Ĉȉ��̖�ɓ�����B
(1) �Ȑ�C�ƍ��W�����ڂ���_�̍��W�����߂�B
(2) �Ȑ�C��x���Cy���ň͂܂ꂽ������x���̂܂���1��]�����Ăł��闧�̂̑̐ς����߂�B
(3) (2)�ŋ��߂��̐ς�V�Ƃ���Ƃ��AV�C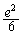 �C
�C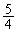 �����������ɕ��ׂ�B�������A
�����������ɕ��ׂ�B�������A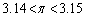 �����
�����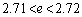 �͊��m�Ƃ���B
�͊��m�Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
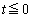 �̂Ƃ��A
�̂Ƃ��A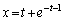 �C
�C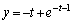 ����A
����A
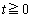 �̂Ƃ��A
�̂Ƃ��A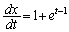 �C
�C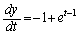 �@(�����̌������Q��)
�@(�����̌������Q��)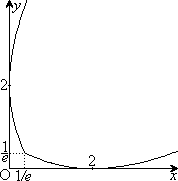
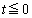 �̂Ƃ��A
�̂Ƃ��A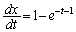 �C
�C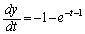
�����\�͈ȉ��̒ʂ�B�܂��Ȑ�C�̃O���t�͉E�}�B| t | (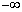 ) ) |
| 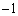 |
| 0 |
| 1 |
| (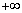 ) ) |
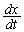 |
| �| | 0 | �{ | �~ | �{ | �{ | �{ |
|
| x | (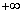 ) ) |  | 0 |  | 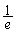 |  | 2 |  | (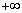 ) ) |
| t | (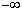 ) ) |
| 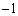 |
| 0 |
| 1 |
| (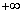 ) ) |
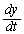 |
| �| | �| | �| | �~ | �| | 0 | �{ |
|
| y | (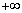 ) ) |  | 2 |  | 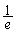 |  | 0 |  | (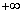 ) ) |
�����\���A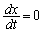 �ƂȂ�̂́A
�ƂȂ�̂́A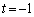 �̂Ƃ��݂̂ŁA���̂Ƃ��A
�̂Ƃ��݂̂ŁA���̂Ƃ��A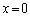 �C
�C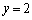 �C
�C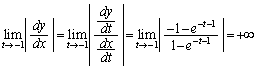 (�}��ϐ��\�����ꂽ���̔����@���Q��)���A�Ȑ�C��
(�}��ϐ��\�����ꂽ���̔����@���Q��)���A�Ȑ�C��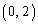 �ɂ�����y���Ɛڂ��܂��B
�ɂ�����y���Ɛڂ��܂��B
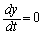 �ƂȂ�̂́A
�ƂȂ�̂́A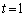 �݂̂ŁA���̂Ƃ��A
�݂̂ŁA���̂Ƃ��A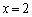 �C
�C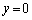 �C
�C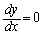 ���A�Ȑ�C��
���A�Ȑ�C��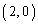 �ɂ�����x���Ɛڂ��܂��B
�ɂ�����x���Ɛڂ��܂��B
����āA���W���Ƃ̐ړ_�́A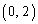 �C
�C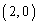 ......[��]�Ȃ��A�����\���A
......[��]�Ȃ��A�����\���A �̂Ƃ�
�̂Ƃ�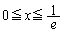 �C
�C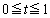 �̂Ƃ�
�̂Ƃ�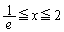
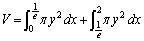 ����B
����B��1���͇A�C��2���͇@�ɂ���u���ϕ����܂��B
��1��(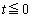 )�ł́A
)�ł́A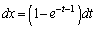 �Cx�F
�Cx�F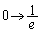 �̂Ƃ�t�F
�̂Ƃ�t�F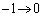
��2��(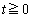 )�ł́A
)�ł́A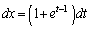 �Cx�F
�Cx�F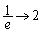 �̂Ƃ�t�F
�̂Ƃ�t�F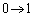
�B�̑�1���́A ����ɁAs��t�ɖ߂��āA
�B�̑�2���́A
�� 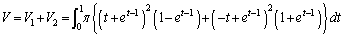 ��ϕ����́A
��ϕ����́A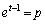 �Ƃ����ƁA
�Ƃ����ƁA
�� 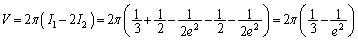 ......[��]
......[��]
(3) 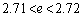 ���A
���A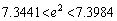
�܂��A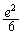 ��
��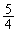 ���r���܂��B
���r���܂��B
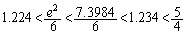 ���A
���A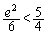 �ł��B
�ł��B
���ɁA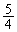 ��V���r���܂��B
��V���r���܂��B 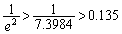 �C
�C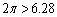 ���A
���A�� 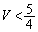
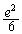 ��V���r���܂��B
��V���r���܂��B �� 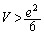 ����āA
����āA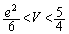 ......[��]
......[��]
���Ȃ��Ă��܂����ł����A���͂��������������ɂ͎^���ł��܂���B
���炭�A�������͌���Ȃ�0�ɋ߂��A�����������͑��̖�肪�قƂ�ł��Ă��Ȃ��ł��傤�B
���i�҂̑唼�����̖���r���Ŏ̂ĂĂ���Ǝv���܂����A�̂Ė��ɂ���A�Ƃ������ƂŁA�������������o�肵�Ă���̂Ȃ�l�����̂ł��B
�E�ϗ͂Ȃǂ��������̂Ȃ�A�ꍇ�����̕��G�Ȗ��Ȃǂ��H�v���ׂ����ƍl���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 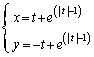
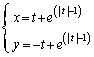
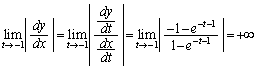 (�}��ϐ��\�����ꂽ���̔����@���Q��)
(�}��ϐ��\�����ꂽ���̔����@���Q��)