���嗝�H���w'06�N[3]
����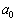 �C
�C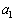 �C
�C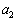 �C��� �͏���
�C��� �͏���
�����Ƃ���B�ȉ��̖�ɓ�����B
(1) ����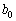 �C
�C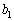 �C
�C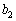 �C��� �����̎��Œ�߂�B
�C��� �����̎��Œ�߂�B 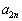 �C
�C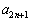 �C
�C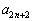 �����ׂĐ��Ȃ��
�����ׂĐ��Ȃ��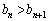 �����藧���Ƃ������B
�����藧���Ƃ������B(2) 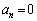 ����n�����邱�Ƃ������B
����n�����邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�́A��Βl���o�Ă��邵�A�����o�Ă���̂ŁA�ǂ�ǂ�ꍇ�������Ă����܂��B(2)�́A���R����1�����݂ɑ��݂��Ă��āA�����̂悤�ɁA�قȂ�2�����̊Ԃɖ����Ɏ��������݂���(�������f�����ƌ����܂�)�킯�ł͂Ȃ��A�Ƃ����Ƃ��납�痈�܂��B�w���@�ŏؖ����Ă݂܂��B
(1) (i) 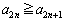 �̂Ƃ��A
�̂Ƃ��A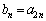
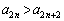 (
(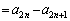 )�@����A
)�@����A
�E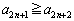 �̂Ƃ��A�@���A
�̂Ƃ��A�@���A �E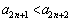 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A ������ɂ��Ă��A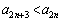 �@����B
�@����B
�E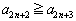 �̂Ƃ��A
�̂Ƃ��A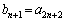
�A���A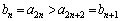
�E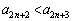 �̂Ƃ��A
�̂Ƃ��A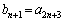
�B���A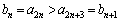
(ii) 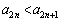 �̂Ƃ��A
�̂Ƃ��A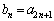
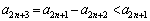 �@����D
�@����D
�E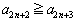 �̂Ƃ��A
�̂Ƃ��A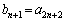
�C���A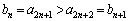
�E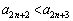 �̂Ƃ��A
�̂Ƃ��A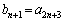
�D���A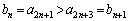
�ȏ���A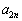 �C
�C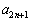 �C
�C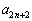 �����ׂĐ��Ȃ��
�����ׂĐ��Ȃ��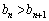 �����藧���܂��B
�����藧���܂��B
(2) 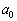 �C
�C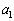 �����R���ŁA
�����R���ŁA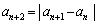 ���A
���A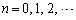 �ɂ��āA
�ɂ��āA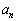 �́A0�C�܂��́A���R���ł��B
�́A0�C�܂��́A���R���ł��B �����ŁA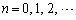 �ɂ��āA���ׂ�
�ɂ��āA���ׂ�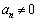 �Ɖ��肷��ƁA��蕶���̒�`���A
�Ɖ��肷��ƁA��蕶���̒�`���A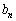 �����ׂĎ��R���@����E �ł��B
�����ׂĎ��R���@����E �ł��B
�܂�(1)���A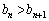 �C�����A
�C�����A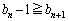
����āA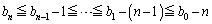
�Ƃ������Ƃ́A�C�ӂ̎��R��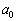 �C
�C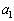 �ɑ��āA
�ɑ��āA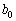 ��
��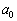 �C
�C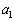 �̏������Ȃ����Ɉ�v���܂����A
�̏������Ȃ����Ɉ�v���܂����A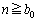 �ƂȂ�悤��n��I�ԂƁA
�ƂȂ�悤��n��I�ԂƁA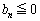 �ƂȂ�A�E�Ɩ������܂��B
�ƂȂ�A�E�Ɩ������܂��B
����āA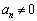 �Ƃ�������͌��ŁA
�Ƃ�������͌��ŁA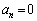 ����n�����݂��܂��B
����n�����݂��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B