���嗝�H���w'08�N[2]
���R��m�Cn�ɑ���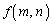 ��
�� �@�@�@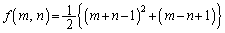
�Œ�߂�B�ȉ��̖�ɓ�����B
(1) 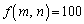 ���݂���m�Cn��1�g���߂�B
���݂���m�Cn��1�g���߂�B (2) a�Cb�Cc�Cd�͐����ŁA����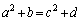 ���݂����Ƃ���B�s����
���݂����Ƃ���B�s����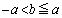 �C
�C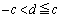 �����藧�Ȃ�A
�����藧�Ȃ�A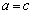 �C
�C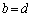 �ƂȂ邱�Ƃ������B
�ƂȂ邱�Ƃ������B (3) �C�ӂ̎��R��k�ɑ��A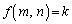 ���݂���m�Cn������1�g�������݂��邱�Ƃ������B
���݂���m�Cn������1�g�������݂��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� ���͈Ӓn�̈����l�ԂȂ̂ŁA���Ȃ�A(1)�́A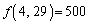 �ɂ��܂����A���Ƃ����킯�ł��Ȃ��A����ł��āA�����������Ȃ��烁�J�j�Y���������A�_���I�\�z�͂����悤�Ƃ������ŁA���́A�ǖ₾�Ǝv���܂��B�Ȃ��A�������Q�Ƃ��Ă��������B
�ɂ��܂����A���Ƃ����킯�ł��Ȃ��A����ł��āA�����������Ȃ��烁�J�j�Y���������A�_���I�\�z�͂����悤�Ƃ������ŁA���́A�ǖ₾�Ǝv���܂��B�Ȃ��A�������Q�Ƃ��Ă��������B
(1) 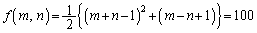
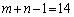 �C
�C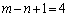
�܂�A
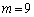 �C
�C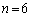
�Ƃ���ƁA
�ƂȂ�A���������̂ŁA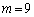 �C
�C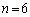 ......[��]
......[��]
(2) 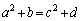 �@����@
�@����@ ���A
��蕶�ɗ^�����Ă�������F
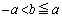 �@����A
�@����A
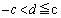 �@����B
�@����B�A�|�B���A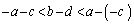 �@(�s�����̏ؖ����Q��)��
�@(�s�����̏ؖ����Q��)�� 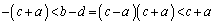 �A���A
�A���A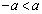 �C�܂�A
�C�܂�A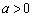 �ł��B�܂��A�B���A
�ł��B�܂��A�B���A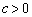 �ł��B�]���āA
�ł��B�]���āA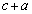 (
(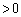 )�Ŋe�ӂ�����ƁA
)�Ŋe�ӂ�����ƁA
(3) �܂��A�C�ӂ̎��R��k�ɑ��A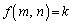 �C�܂�A
�C�܂�A �Ƃ��āA
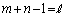 �C
�C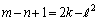
�ƂȂ鐮��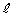 �����������Ƃ��܂��B
�����������Ƃ��܂��B
����2����A������m�Cn�ɂ��ĉ����ƁA 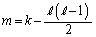 �C
�C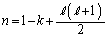
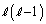 �C
�C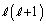 �͘A��2�����̐ςȂ̂ŋ����ł����āA
�͘A��2�����̐ςȂ̂ŋ����ł����āA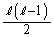 �C
�C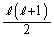 �͐����ł��B�]���āAm�Cn�͐����ł��B�����ŁA
�͐����ł��B�]���āAm�Cn�͐����ł��B�����ŁA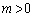 �C
�C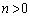 �ł��邽�߂ɂ́A
�ł��邽�߂ɂ́A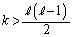 �C
�C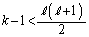
�łȂ���Ȃ�܂���B2�Ԗڂ̕��̕s�����́Ak�C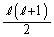 �������ł��邱�Ƃ���A
�������ł��邱�Ƃ���A �Ɠ��l�ŁA���ǁA
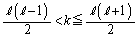 �@����C
�@����C�����������悢���ƂɂȂ�܂��B�]���āAm�Cn�����Ȃ��Ƃ�1�g���݂��邱�Ƃ��������߂ɂ́A�C����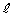 �����݂��邱�Ƃ������悢���ƂɂȂ�܂��B
�����݂��邱�Ƃ������悢���ƂɂȂ�܂��B
�C�̍��̕s��������A �� 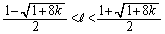 �@����D
�@����D
�C�̉E�̕s��������A �� 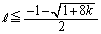 �C
�C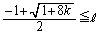 �@����E
�@����E
�D ���� �E���A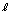 �����R���Ƃ���A
�����R���Ƃ���A 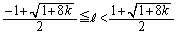 �@����F
�@����F���̋�Ԃ̕���1�Ȃ̂ŇF���݂������R���͕K�����݂��܂��B
���ǁA�ؖ��̃X�g�[���[�͈ȉ��̂悤�ɂȂ�܂��B
�C�ӂ̎��R��k�ɑ��āA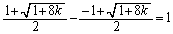 ���A
���A 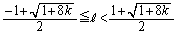 �@����F
�@����F�������R��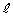 ���K�����݂��܂��B
���K�����݂��܂��B
�F�̍��̕s�������A ���ӂ�2�悵�āA
�� 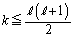 �F�̉E�̕s�������A
�F�̉E�̕s�������A 2�悵�Đ�������ƁA
�]���āA�C�ӂ̎��R��k�ɑ��āA
�������R��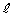 ���K�����݂��܂��B���̂Ƃ��A
���K�����݂��܂��B���̂Ƃ��A 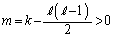 �C
�C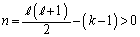
�Ƃ����A
�����܂��B
���ɁA�C�ӂ̎��R��k�ɑ��A2�g�̎��R��m�Cn��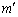 �C
�C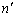 �������Ă����Ƃ��ɁA
�������Ă����Ƃ��ɁA �܂�A
�Ƃ��܂��B
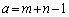 �C
�C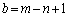 �C
�C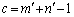 �C
�C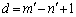 �Ƃ����ƁA�@�����܂��Bm�Cn�͎��R���Ȃ̂ŁA
�Ƃ����ƁA�@�����܂��Bm�Cn�͎��R���Ȃ̂ŁA ����āA�A�C�B�����������̂ŁA(2)���A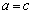 �C
�C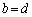
�܂�A ����āA�C�ӂ̎��R��k�ɑ��A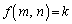 ���݂���m�Cn������1�g�������݂��܂��B
���݂���m�Cn������1�g�������݂��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B