早大理工数学'10年[2]
xy平面上の点 に対して、点
に対して、点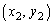 ,
, ,・・・ を次の式で順に定める。
,・・・ を次の式で順に定める。
以下の問いに答えよ。
(1) 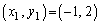 のとき、
のとき、 を求めよ。
を求めよ。 (2) 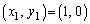 のとき、
のとき、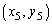 を求めよ。
を求めよ。 (4)  となる2以上の整数nが存在しないとき、点
となる2以上の整数nが存在しないとき、点 はどのような範囲にあるかを図示せよ。
はどのような範囲にあるかを図示せよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 問題文に行列が出てきますが、行列や1次変換の問題というほどのことはありません。
第1象限、第4象限、・・・、x軸上 の部分、y軸上
の部分、y軸上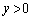 の部分、・・・、という具合に分けて考えるように促す誘導に即して考えます。面倒ですが、すべての場合を調べても試験時間内にやりきれるでしょう。
の部分、・・・、という具合に分けて考えるように促す誘導に即して考えます。面倒ですが、すべての場合を調べても試験時間内にやりきれるでしょう。
これは、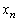 と
と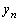 を入れ替えて
を入れ替えて にマイナスをつける(図形的には、反時計回りに
にマイナスをつける(図形的には、反時計回りに 回転することを意味する)、ということです。
回転することを意味する)、ということです。 ・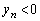 のとき、
のとき、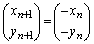
これは、 と
と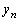 の双方にマイナスをつける(図形的には、反時計回りにπ回転することを意味する)、ということです。
の双方にマイナスをつける(図形的には、反時計回りにπ回転することを意味する)、ということです。 以上の規則で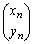 から
から を求めることを、
を求めることを、 →
→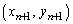 のように表すことにします。
のように表すことにします。
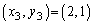 ......[答]このまま続けていくと、
......[答]このまま続けていくと、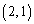 →
→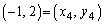 となり、
となり、 となっています。
となっています。
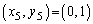 ......[答]
......[答] となっています。
となっています。
(3) 以下では、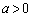 ,
,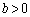 とします。
とします。
 →
→ →
→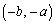 →
→ →
→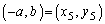
∴ 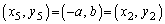 これより、
これより、 では
では ,
,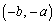 ,
, が循環的に現れ、kを自然数として、
が循環的に現れ、kを自然数として、
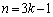 のとき
のとき ,
,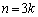 のとき
のとき ,
, のとき
のとき
よって、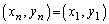 となる2以上の整数nは存在しません。
となる2以上の整数nは存在しません。 →
→ →
→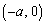 →
→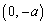 →
→
∴  これより、
これより、 では
では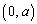 ,
,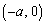 ,
, が循環的に現れ、kを自然数として、
が循環的に現れ、kを自然数として、
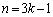 のとき
のとき ,
, のとき
のとき ,
,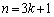 のとき
のとき
よって、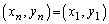 となる2以上の整数nは存在しません。
となる2以上の整数nは存在しません。・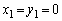 のとき、
のとき、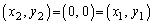
これより、すべての整数 について、
について、
 (3)を含めて以上より、
(3)を含めて以上より、
“ となる2以上の整数nが存在しない”
となる2以上の整数nが存在しない”⇔ “ かつ
かつ 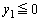 ”
” 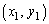 の存在範囲を図示すると右図黄緑色着色部(太線を含み、点線と白マルを除く)。
の存在範囲を図示すると右図黄緑色着色部(太線を含み、点線と白マルを除く)。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 