���嗝�H���w'10�N[5]
�\�̏o��m����p (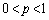 )�C���̏o��m����
)�C���̏o��m���� �̍d�݂�1������Bn�����R���Ƃ���B���̍d�݂�
�̍d�݂�1������Bn�����R���Ƃ���B���̍d�݂�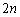 �����Ƃ��A�\��
�����Ƃ��A�\�� ��ȏ�o��m����
��ȏ�o��m���� �Ƃ���B�ȉ��̖₢�ɓ�����B
�Ƃ���B�ȉ��̖₢�ɓ�����B
(1) 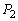 �C
�C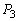 �����߂�B
�����߂�B (2)  �ƂȂ�p�͈̔͂����߂�B
�ƂȂ�p�͈̔͂����߂�B (3) 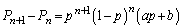 �ƂȂ�a�Cb��n��p���ĕ\���B������a�Cb��p���܂܂Ȃ��Ƃ���B
�ƂȂ�a�Cb��n��p���ĕ\���B������a�Cb��p���܂܂Ȃ��Ƃ���B (4)  �̂Ƃ��A
�̂Ƃ��A ���ő�ɂ���n�����߂�B
���ő�ɂ���n�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����m���̓����o�肵�Ă������嗝�H�̖ʖږ��@�A�����[���V�X�����ł��B
(1) 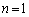 �̂Ƃ��A�d�݂�2���āA�\��2��ȏ�o��m��
�̂Ƃ��A�d�݂�2���āA�\��2��ȏ�o��m�� �́A
�́A 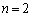 �̂Ƃ��A�d�݂�4���āA�\��3��ȏ�o��m��
�̂Ƃ��A�d�݂�4���āA�\��3��ȏ�o��m��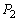 �́A�\��3��o��m����
�́A�\��3��o��m���� �C�\��4��o��m����
�C�\��4��o��m���� �C����āA
�C����āA �̂Ƃ��A�d�݂�6���āA�\��4��ȏ�o��m��
�̂Ƃ��A�d�݂�6���āA�\��4��ȏ�o��m�� �́A�\��4��o��m����
�́A�\��4��o��m���� �C�\��5��o��m����
�C�\��5��o��m����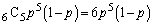 �C�\��6��o��m����
�C�\��6��o��m����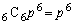 �C����āA
�C����āA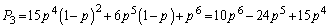 ......[��]
......[��]
(2) (1)�̌��ʂ�p���āA
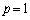 �̂Ƃ��A
�̂Ƃ��A �ƂȂ�̂ŁA�J�b�R����
�ƂȂ�̂ŁA�J�b�R����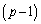 �Ŋ����܂��B
�Ŋ����܂��B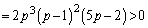 �@����@
�@����@ ���A
���A ......[��]
......[��]
(3) �d�݂�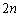 �����Ƃ��A�\��
�����Ƃ��A�\��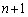 ��ȏ�o��m��
��ȏ�o��m�� �́A�\��
�́A�\��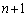 ��o��m���A�\��
��o��m���A�\�� ��o��m���A����A�\��
��o��m���A����A�\��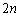 ��o��m�����������킹�āA
��o��m�����������킹�āA �ƕ\���܂����A�������ʓI��p�̐����ŕ\���͍̂���ł��B�����ŁA(1)�̌��ʂ��g���ė\�����Ă݂܂��B
������A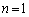 �̂Ƃ��A
�̂Ƃ��A �C
�C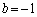 �ł��B
�ł��B
�@���A ������A �̂Ƃ��A
�̂Ƃ��A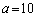 �C
�C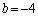 �ł��B
�ł��B
���ꂾ���ł́A��ʓI��n�ɂ��ė\������͓̂���ł����A���ɖ��������� ���A
���A �Ƃ��Čv�Z���A
���A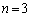 �̂Ƃ��A
�̂Ƃ��A �C
�C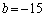 �Ƌ��߂Ă݂Ă��A�s�\�Ƃ����킯�ł͂���܂��A��͂�\������̂͌������ł��傤�B���ɗ\���ł����Ƃ��āA���w�I�A�[�@�łǂ��������A�Ƃ������Ƃ��ۑ�ɂȂ�܂��B
�Ƌ��߂Ă݂Ă��A�s�\�Ƃ����킯�ł͂���܂��A��͂�\������̂͌������ł��傤�B���ɗ\���ł����Ƃ��āA���w�I�A�[�@�łǂ��������A�Ƃ������Ƃ��ۑ�ɂȂ�܂��B
���w�I�A�[�@�̘g�g�݂ɏ悹�邽�߂ɂ́A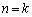 �̏ꍇ����
�̏ꍇ���� �̏ꍇ�ւǂ��Ȃ��邩�A�Ƃ������Ƃ��l����K�v������܂��B���̂��߂�
�̏ꍇ�ւǂ��Ȃ��邩�A�Ƃ������Ƃ��l����K�v������܂��B���̂��߂�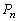 ��
�� �̂Ȃ�����l���Ă݂܂��B
�̂Ȃ�����l���Ă݂܂��B
 �͍d�݂�
�͍d�݂� ����
����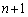 ��ȏ�\���o��(�ȉ��A������u�����v�ƌ������Ƃɂ��܂�)�m���ł����A
��ȏ�\���o��(�ȉ��A������u�����v�ƌ������Ƃɂ��܂�)�m���ł����A ����
����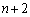 ��ȏ�\���o��ƁA
��ȏ�\���o��ƁA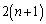 ���Ă��u�����v�͖���Ă��܂��B�Ƃ������Ƃ́A
���Ă��u�����v�͖���Ă��܂��B�Ƃ������Ƃ́A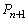 ����
����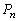 �������ƁA
�������ƁA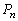 �̂�����
�̂����� ��ȏ�\���o��m��
��ȏ�\���o��m��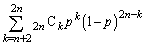 �͏����������ƂɂȂ�܂��B�ł����A
�͏����������ƂɂȂ�܂��B�ł����A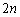 ����
����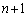 ��\���o���ꍇ�ł��A����2��̂ǂ��炩�A���邢�́A2��Ƃ��\���o���
��\���o���ꍇ�ł��A����2��̂ǂ��炩�A���邢�́A2��Ƃ��\���o��� ���āu�����v�ł��܂��B����Ɍ����A
���āu�����v�ł��܂��B����Ɍ����A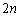 ���āu�����v�ł��Ȃ������ꍇ�ł��An��\���o�Ă���A����2��̂ǂ�����\�ł���A
���āu�����v�ł��Ȃ������ꍇ�ł��An��\���o�Ă���A����2��̂ǂ�����\�ł���A ���āu�����v�ł��܂��B
���āu�����v�ł��܂��B
�����Ő������܂��B�d�݂� ���āA�\��n��o�鎖�ۂ��u����A�v�C�\��
���āA�\��n��o�鎖�ۂ��u����A�v�C�\�� ��o�鎖�ۂ��u����B�v�C�\��
��o�鎖�ۂ��u����B�v�C�\��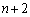 ��ȏ�o�鎖�ۂ��u����C�v�Ƃ��A����A�C����B�C����C���N����m����
��ȏ�o�鎖�ۂ��u����C�v�Ƃ��A����A�C����B�C����C���N����m����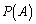 �C
�C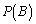 �C
�C �Ƃ���ƁA
�Ƃ���ƁA
�d�݂�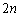 ���Đ�������̂́A����B�C����C���N�����ꍇ�ŁA���̊m��
���Đ�������̂́A����B�C����C���N�����ꍇ�ŁA���̊m��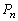 �ɂ��āA
�ɂ��āA �d�݂� ���Đ�������̂́A����A���N���Ă�����2��̂ǂ�����\���o���ꍇ�ƁA����B���N���Ă�����2��̂ǂ��炩�A���邢�́A2��Ƃ��\���o��ꍇ�ƁA����C���N�����ꍇ�ŁA���̊m��
���Đ�������̂́A����A���N���Ă�����2��̂ǂ�����\���o���ꍇ�ƁA����B���N���Ă�����2��̂ǂ��炩�A���邢�́A2��Ƃ��\���o��ꍇ�ƁA����C���N�����ꍇ�ŁA���̊m�� �ɂ��āA
�ɂ��āA ������A
 �@����A
�@����A�Ƃ���ŁA����A���N����m�� �́A
�́A ����B���N����m��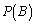 �́A
�́A �A�ɑ�����āA
����ŁA���w�I�A�[�@���g�����ƂȂ��Aa�Cb�����߂��܂����B
 �C
�C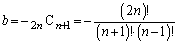 ......[��]
......[��]
(4) 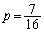 �̂Ƃ��A
�̂Ƃ��A
������A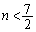 �C�����A
�C�����A �̂Ƃ��A
�̂Ƃ��A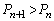
 �C�����A
�C�����A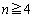 �̂Ƃ��A
�̂Ƃ��A
�� 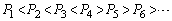 ����āA
����āA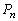 ���ő�ɂ���n�́A
���ő�ɂ���n�́A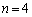 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B