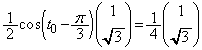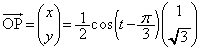���嗝�H���w'11�N[2]
xy-���ʏ�̉~C�F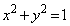 �̓����a
�̓����a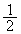 �̉~D��C�ɐڂ��Ȃ��炷�ׂ炸�ɓ]����B����t�ɂ�����D�͓_
�̉~D��C�ɐڂ��Ȃ��炷�ׂ炸�ɓ]����B����t�ɂ�����D�͓_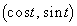 ��C�ɐڂ��Ă���Ƃ���BD�̎���̓_P�̋O�Ղɂ��čl����B���鎞��
��C�ɐڂ��Ă���Ƃ���BD�̎���̓_P�̋O�Ղɂ��čl����B���鎞��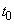 �ɂ����ē_P��
�ɂ����ē_P��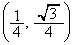 �ɂ���AD�̒��S����2�ی��ɂ���Ƃ���B�ȉ��̖₢�ɓ�����B
�ɂ���AD�̒��S����2�ی��ɂ���Ƃ���B�ȉ��̖₢�ɓ�����B
(1) ����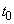 �ɂ�����D�̒��S�̍��W�����߂�B
�ɂ�����D�̒��S�̍��W�����߂�B (2) ��1�ی��ɂ����āA�_P��C��ɂ���Ƃ���P�̍��W�����߂�B
(3) �_P�̋O�Ղ�xy-���ʏ�ɐ}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�~�̓�����]���������̉~�̎���̓_�̋O�Ղ́A�ӂ��A�n�C�|�T�C�N���C�h�ɂȂ�܂��B�{��ł́A������Ɛ}��`���Ă݂�A����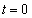 ��
��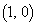 �ɂ������~D��̓_���Ax�����
�ɂ������~D��̓_���Ax����� �̕��������Ƃ͂����킩��܂��B�_P���ŏ��ɂǂ��ɂ����̂����킩��Ȃ��̂ł����A�ŏ��̈ʒu�ƒ��S�����Ԕ��a��x���ƂȂ��p��α�Ƃ����A�n�C�|�T�C�N���C�h�̗ޑ�Ɠ����悤�ɍl���čs���܂��B
�̕��������Ƃ͂����킩��܂��B�_P���ŏ��ɂǂ��ɂ����̂����킩��Ȃ��̂ł����A�ŏ��̈ʒu�ƒ��S�����Ԕ��a��x���ƂȂ��p��α�Ƃ����A�n�C�|�T�C�N���C�h�̗ޑ�Ɠ����悤�ɍl���čs���܂��B
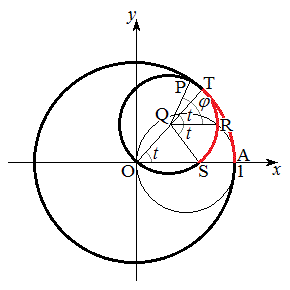 (1) ����t�ɂ�����~D�̒��S�̈ʒu��Q�C Q��ʂ�x���ɕ��s�Ȓ����Ɖ~D�Ƃ̌�_�̂����Ax���W�̑傫������R�Ƃ���
(1) ����t�ɂ�����~D�̒��S�̈ʒu��Q�C Q��ʂ�x���ɕ��s�Ȓ����Ɖ~D�Ƃ̌�_�̂����Ax���W�̑傫������R�Ƃ���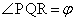 �C�ړ_
�C�ړ_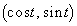 ��T�Ƃ��܂��B
��T�Ƃ��܂��BQ�CT�CO�͈꒼����ɂ���̂ŁA����t�ɂ�����Q�̍��W��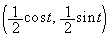 �ł��B�܂��A
�ł��B�܂��A 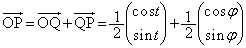 �@����@
�@����@����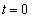 �ɂ����Đړ_T�͓_A
�ɂ����Đړ_T�͓_A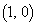 �ɂ���܂��B���̂Ƃ��A
�ɂ���܂��B���̂Ƃ��A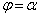 (
(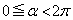 )�Ƃ��܂��BD��̓_�Ŏ���
)�Ƃ��܂��BD��̓_�Ŏ���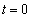 ��A
��A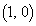 �Ɉʒu���Ă����_��S�Ƃ���ƁA����t�ɂ����āA�~D��̉~��TS�Ɖ~C��̉~��TA�̒����͓������̂ŁA
�Ɉʒu���Ă����_��S�Ƃ���ƁA����t�ɂ����āA�~D��̉~��TS�Ɖ~C��̉~��TA�̒����͓������̂ŁA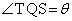 �Ƃ���ƁA
�Ƃ���ƁA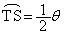 �C
�C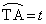 (��ʊp���Q��)���A
(��ʊp���Q��)���A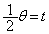 �C
�C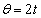
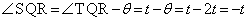
������A����t�ɂ����āA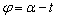
�@�ɑ�����āA 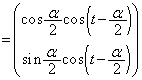 �@����A
�@����AP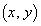 �́A
�́A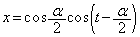 �C
�C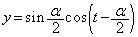 �C������AP�͒���
�C������AP�͒���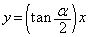 ��ɂ���܂��B�܂��A
��ɂ���܂��B�܂��A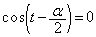 �̂Ƃ��ɂ́A�_P�͌��_O�ɗ��܂��BP�͎���
�̂Ƃ��ɂ́A�_P�͌��_O�ɗ��܂��BP�͎���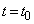 ��
��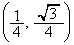 �ɗ���̂ŁA
�ɗ���̂ŁA �� 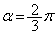 �A�ɑ�����āA
�A�ɑ�����āA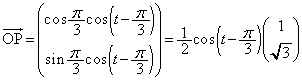 �@����B
�@����B
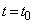 �ł́A
�ł́A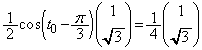
����āA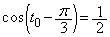
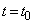 �ɂ����āAD�̒��SQ����2�ی��ɂ��邱�Ƃ���A
�ɂ����āAD�̒��SQ����2�ی��ɂ��邱�Ƃ���A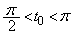 �C
�C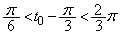
�� 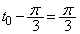 ��
�� 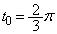
D�̒��SQ�̍��W�́A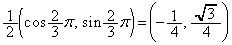 ......[��]
......[��]
(2) �_P�͒���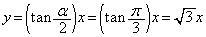 ��̓_�ł����A���̒����Ɖ~C�Ƃ̌�_�́A
��̓_�ł����A���̒����Ɖ~C�Ƃ̌�_�́A 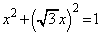 �C
�C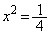
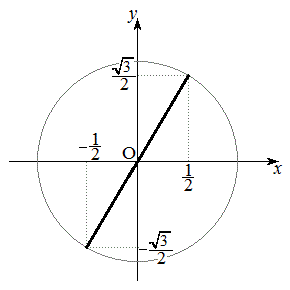
(3) �B���A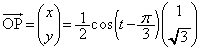
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 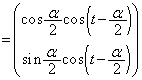 �@����A
�@����A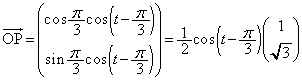 �@����B
�@����B