����c��w��E�n���E��i���H�w��2011�N���w�������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@xy-���ʏ�̕�����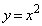 ��C�Ƃ���B�ȉ��̖₢�ɓ�����B
��C�Ƃ���B�ȉ��̖₢�ɓ�����B
(1) C��̓_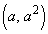 �ɂ�����C�̖@���̕����������߂�B
�ɂ�����C�̖@���̕����������߂�B (2) �_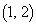 ��ʂ�@���̐������߂�B
��ʂ�@���̐������߂�B (3) �_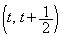 ��ʂ�C�̖@���̐���2�ƂȂ邽�߂�t �ɑ�����������߂�B
��ʂ�C�̖@���̐���2�ƂȂ邽�߂�t �ɑ�����������߂�B [��]
[2]�@xy-���ʏ�̉~C�F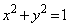 �̓����a
�̓����a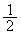 �̉~D��C�ɐڂ��Ȃ��炷�ׂ炸�ɓ]����B����t�ɂ�����D�͓_
�̉~D��C�ɐڂ��Ȃ��炷�ׂ炸�ɓ]����B����t�ɂ�����D�͓_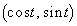 ��C�ɐڂ��Ă���Ƃ���BD�̎���̓_P�̋O�Ղɂ��čl����B���鎞��
��C�ɐڂ��Ă���Ƃ���BD�̎���̓_P�̋O�Ղɂ��čl����B���鎞��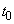 �ɂ����ē_P��
�ɂ����ē_P��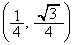 �ɂ���AD�̒��S����2�ی��ɂ���Ƃ���B�ȉ��̖₢�ɓ�����B
�ɂ���AD�̒��S����2�ی��ɂ���Ƃ���B�ȉ��̖₢�ɓ�����B
(1) ����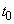 �ɂ�����D�̒��S�̍��W�����߂�B
�ɂ�����D�̒��S�̍��W�����߂�B (2) ��1�ی��ɂ����āA�_P��C��ɂ���Ƃ���P�̍��W�����߂�B
(3) �_P�̋O�Ղ�xy-���ʏ�ɐ}������B
[��]
[3]�@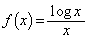 �Ƃ���B�ȉ��̖₢�ɓ�����B
�Ƃ���B�ȉ��̖₢�ɓ�����B
(1) 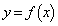 �̃O���t�̊T�`�����̓_�ɒ��ӂ��ĕ`���F
�̃O���t�̊T�`�����̓_�ɒ��ӂ��ĕ`���F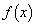 �̑����A�O���t�̉��ʁA
�̑����A�O���t�̉��ʁA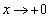 �C
�C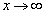 �̂Ƃ���
�̂Ƃ���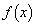 �̋����B
�̋����B (2) n�����R���Ƃ���B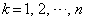 �ɑ���x��
�ɑ���x��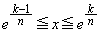 ���Ƃ���
���Ƃ���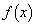 �̍ő�l��
�̍ő�l��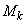 �C�ŏ��l��
�C�ŏ��l��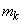 �Ƃ��A
�Ƃ��A �Ƃ����B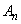 �C
�C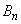 �����߂�B
�����߂�B (3) 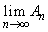 �����
�����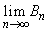 �����߂�B
�����߂�B (4) �en�ɑ���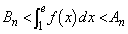 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B [��]
[4]�@xy-���ʏ�̌��_��O�Ƃ��A�ȉ~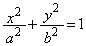 (
(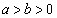 )��E�Ƃ���BE��̓_P
)��E�Ƃ���BE��̓_P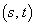 �ɂ�����E�̖@����x���Ƃ̌�_��Q�Ƃ���B�_P��
�ɂ�����E�̖@����x���Ƃ̌�_��Q�Ƃ���B�_P��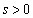 �C
�C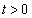 �͈̔͂��Ƃ��A
�͈̔͂��Ƃ��A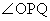 ���ő�ɂȂ�_P�����߂�B
���ő�ɂȂ�_P�����߂�B
[��]
[5]�@�l�ʑ�OABC�ɂ�����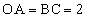 �C
�C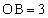 �C
�C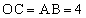 �C
�C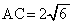 �ł���B�܂��A
�ł���B�܂��A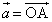 �C
�C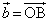 �C
�C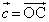 �Ƃ���B�ȉ��̖₢�ɓ�����B
�Ƃ���B�ȉ��̖₢�ɓ�����B
 (2) ��OAB���܂ޕ��ʂ�H�Ƃ���BH��̓_P�Œ���PC��H������������̂��Ƃ�B���̂Ƃ��A
(2) ��OAB���܂ޕ��ʂ�H�Ƃ���BH��̓_P�Œ���PC��H������������̂��Ƃ�B���̂Ƃ��A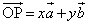 �ƂȂ�x�Cy�����߂�B
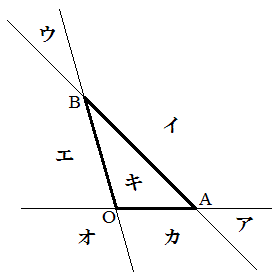
�ƂȂ�x�Cy�����߂�B(3) ����H��OA�CAB�CBO�ʼnE�}�̂悤��7�̗̈�A�C�C�C�E�C�G�C�I�C�J�C�L�ɂ킯��B�_P�͂ǂ̗̈�ɓ��邩������B (4) ��AB�Ł�ABC�Ɓ�OAB�̂Ȃ��p�͉s�p�ɂȂ邩�A���p�ɂȂ邩�A����Ƃ��݊p�ɂȂ邩�肹��B�������A1�ӂ����L����2�̎O�p�`�̂Ȃ��p�Ƃ́A���L����ӂɒ������镽�ʂł�2�̎O�p�`�̐���̂Ȃ��p�̂��Ƃł���B
[��]
�e�⌟��
[1](��������)�@�@�����o�Ă��܂����A�����I�ɐ��w�U�͈̔͂̔����̖��ł��B�_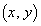 ����A3�����̃O���t��3�{�̐ڐ���������Ƃ��A�_
����A3�����̃O���t��3�{�̐ڐ���������Ƃ��A�_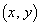 �̑��ݔ͈͂����߂�悤�Ȗ��(�эL�{�Y��08�N[2])�ł́A�{��Ɠ��l�̉�@�ʼn������ƂɂȂ�܂��B�����������́A���w�V�܂ŗ��C���闝�n�������n���̕������ӂɂ��邱�Ƃ������̂ł����A���H�n��w�ł��o�肳��邱�Ƃ�����܂��B���w�V���C�҂��K���o�����Ă����ׂ��^�C�v�̖��ł��B
�̑��ݔ͈͂����߂�悤�Ȗ��(�эL�{�Y��08�N[2])�ł́A�{��Ɠ��l�̉�@�ʼn������ƂɂȂ�܂��B�����������́A���w�V�܂ŗ��C���闝�n�������n���̕������ӂɂ��邱�Ƃ������̂ł����A���H�n��w�ł��o�肳��邱�Ƃ�����܂��B���w�V���C�҂��K���o�����Ă����ׂ��^�C�v�̖��ł��B
�{��ł́A(3)�̓r���ɏo�Ă���3���������F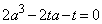 �ŁA�萔t �����āA
�ŁA�萔t �����āA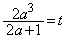 �Ƃ���A���w�V�͈̖̔͂��ɂȂ�܂��B���n���́A�������������P���ł��Ղ������m��܂���B�����A�K���������܂��萔�������ł���킯�ł͂Ȃ��̂ŁA���w�U�ʼn������@���K�{�ł��B
�Ƃ���A���w�V�͈̖̔͂��ɂȂ�܂��B���n���́A�������������P���ł��Ղ������m��܂���B�����A�K���������܂��萔�������ł���킯�ł͂Ȃ��̂ŁA���w�U�ʼn������@���K�{�ł��B
[2](��������)�@�ɂ������܂������A�~�̓�����]���������̉~�̉~����̓_�̋O�Ղ́A�ӂ��A�n�C�|�T�C�N���C�h�ɂȂ�܂��B�A���A�{��ł͂�⎖��قȂ�܂��B�o��҂́A�v�Z���ȒP�ɂ��邽�߂ɁA�ʏ�̖��Ɛݒ��ς����Ǝv���܂����A���ɂƂ��ẮA��₠�肪�����f�ŁA���������Ȃ��A�Ǝ�����ł܂��������������̂ł͂Ȃ����Ǝv���܂��B
���������čl����A�ނ�������Ղ��Ȃ�悤�ɔz������Ă���̂ŁA���������j�𗧂Ă��̂ł���A���M�������ė�Âɉ����i�߂�悢�̂ł��B�ނ���A���܂ʼn����Ă�������A�펯�I�Ȃ��Ƃ���A�o���I�Ȃ��ƂȂǂɉe�����ꂸ�ɁA�ڂ̑O�̖��ƌ��������ĉ����ׂ��ł��Bx�̕������F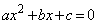 ������1�̉������A�ƌ���ꂽ�Ƃ��ɁA����͏d���ŁA
������1�̉������A�ƌ���ꂽ�Ƃ��ɁA����͏d���ŁA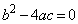 �̂Ƃ����A�ƌ��߂��Ă͂Ȃ�Ȃ��̂ł��B
�̂Ƃ����A�ƌ��߂��Ă͂Ȃ�Ȃ��̂ł��B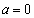 �C
�C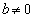 �ł���A1���������ŁA�������͂���1�̉����������܂���B
�ł���A1���������ŁA�������͂���1�̉����������܂���B
���̐��E�̎��ۂ̒��ɂ́A�����������ǂ�Ȃɕ���ςݏd�˂Ă����Ǝ��M�������Ă��Ă��A���̌o���͈̔͂ł͋y�Ȃ��悤�ȓ��قȎ��ۂ���������܂��B���m�̐��E�A���m�̖�肪���݂��邱�Ƃ�f���Ɏ���āA�\���Ɏז�����邱�ƂȂ��A�ڂ̑O�̖��ɗ�Ò����Ɍ��������悤�ɂ��܂��傤�B
[3](��������)�@�Ֆ�Ƃ����킯�ł͂���܂��A�悭�����Ă������ł���Ύ肪�~�܂�Ƃ���͂Ȃ��A�Ƃ������ł��B���x�ȎZ�I�͕K�v�ł͂���܂���B���ȏ����x���̂��Ƃ��m���ɐg�ɂ��Ă��邩�A�Ƃ������Ƃ�����Ă��܂��B�K�x�ȃ{�����[��������A�v�Z���K�ɂ͐�D�̖��ƌ����܂��B
�{��ł��C�ɂȂ�̂́A��蕶�ɓ��i�̒��ӏ������Ȃ��A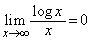 ��O��Ƃ��Ă悢�̂��A�Ƃ������Ƃł��B�������ł́A�܂��͒m���Ƃ��ė��p�����A�Ƃ��ē��Ă������Ă����A���ԓI�]�T������A�ؖ������Ă����A�Ƃ������Ƃł悢�Ǝv���܂��B
��O��Ƃ��Ă悢�̂��A�Ƃ������Ƃł��B�������ł́A�܂��͒m���Ƃ��ė��p�����A�Ƃ��ē��Ă������Ă����A���ԓI�]�T������A�ؖ������Ă����A�Ƃ������Ƃł悢�Ǝv���܂��B
�ł́A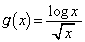 �Ƃ������̑����ׂāA
�Ƃ������̑����ׂāA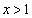 �ɂ����āA
�ɂ����āA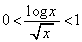 ���A���ӂ�
���A���ӂ�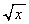 �ł���āA
�ł���āA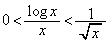 ��
��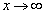 �Ƃ��Ă͂��݂������g���܂����B
�Ƃ��Ă͂��݂������g���܂����B
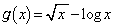 �̑����ׂāA
�̑����ׂāA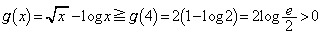 ����A
����A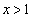 �ɂ�����
�ɂ����� �Ƃ��čs�����Ƃ��ł��܂��B
�Ƃ��čs�����Ƃ��ł��܂��B
���ɂ��A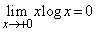 ��
��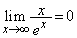 �Ȃǂ��K�v�ɂȂ�ꍇ������܂��B�������Ŏ��Ԃ������A
�Ȃǂ��K�v�ɂȂ�ꍇ������܂��B�������Ŏ��Ԃ������A
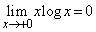 �́A
�́A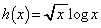 �̑����ׁA
�̑����ׁA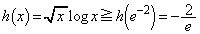 ��
��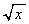 �������āA
�������āA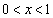 �ɂ����āA
�ɂ����āA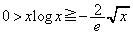 ��
��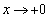 �Ƃ��Ă͂��݂������g���Γ����܂��B
�Ƃ��Ă͂��݂������g���Γ����܂��B
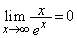 �́A
�́A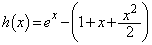 �Ƃ����A
�Ƃ����A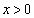 �ɂ����āA
�ɂ����āA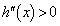 �C
�C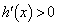 �C
�C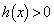 �����������A
�����������A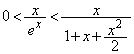 ��
��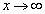 �Ƃ��Ă͂��݂������g���Γ����܂��B
�Ƃ��Ă͂��݂������g���Γ����܂��B
[4](��������)�@�ȉ~����ނƂ��Ď��グ���Ă��܂����A�ڐ��̕��������g�����x�ŁA�ȉ~�Ƃ��Ă̐������g���킯�ł͂Ȃ��A�����������o���܂ł��Ȃ��ő�ŏ��̖��ł��B�ł́A���ڂ̉��@�藝�Ƒ������ρE���敽�ς̊W��p���Ă��܂��B�ȉ~��2�����̂Ȃ��p���l���邠����͋��ȏ����x���̊�{���ƌ����܂����A�������ρE���敽�ς̎g�����ɂ͏��X���ӂ��K�v�ł��B
�{��ł́A2�����̂Ȃ��p�̐��ڂ��A�ȉ~��̓_�̍��W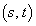 ��x���W��y���W�̐�
��x���W��y���W�̐�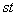 �Ɉˑ����ĕω����܂��B2�����̂Ȃ��p�̍ő���A
�Ɉˑ����ĕω����܂��B2�����̂Ȃ��p�̍ő���A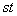 �ő�Ƃ��čl���邱�ƂɂȂ�܂����A
�ő�Ƃ��čl���邱�ƂɂȂ�܂����A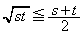 �Ƃ����`�ő������ρE���敽�ς̊W�𗘗p���邱�Ƃ͂ł��܂���B�Ȃ����ƌ����ƁA
�Ƃ����`�ő������ρE���敽�ς̊W�𗘗p���邱�Ƃ͂ł��܂���B�Ȃ����ƌ����ƁA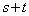 �����l�ɂȂ�Ȃ�����ł��B
�����l�ɂȂ�Ȃ�����ł��B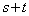 �����lc�ɂȂ�ł���A
�����lc�ɂȂ�ł���A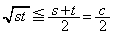 �Ƃ��āA�u
�Ƃ��āA�u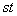 ��
��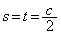 �̂Ƃ��ő�l
�̂Ƃ��ő�l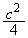 ���Ƃ�v�Ƃ��邱�Ƃ��ł��܂��B�������A�{��ł�
���Ƃ�v�Ƃ��邱�Ƃ��ł��܂��B�������A�{��ł�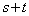 �͒萔�ɂȂ�܂���B
�͒萔�ɂȂ�܂���B
�Ⴆ�A�u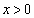 �C
�C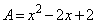 �C
�C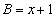 �̂Ƃ��A
�̂Ƃ��A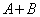 �̍ŏ��l�����߂�B�v�Ƃ��������A�������ρE���敽�ς̊W��p���āA
�̍ŏ��l�����߂�B�v�Ƃ��������A�������ρE���敽�ς̊W��p���āA
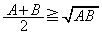 (������
(������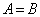 �̂Ƃ�����)�@���(��)�@���A
�̂Ƃ�����)�@���(��)�@���A
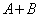 �́A
�́A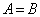 �C�����A
�C�����A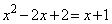 �C
�C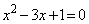 �C
�C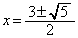 �̂Ƃ��A�ŏ��l�F
�̂Ƃ��A�ŏ��l�F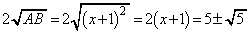 (����������
(����������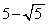 ���Ƃ�ׂ��ł��傤��)���Ƃ�B
���Ƃ�ׂ��ł��傤��)���Ƃ�B
�ȂǂƂ���̂͊ԈႢ�ł��B�Ȃ��Ȃ�A(��)�̉E��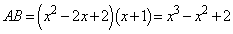 ���萔�ɂȂ�Ȃ�����ł��B
���萔�ɂȂ�Ȃ�����ł��B
�������́A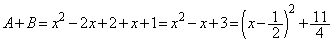 �́A
�́A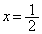 �̂Ƃ��ɍŏ��l�F
�̂Ƃ��ɍŏ��l�F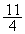 ���Ƃ�܂��B
���Ƃ�܂��B
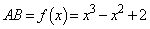 �Ƃ���ƁA
�Ƃ���ƁA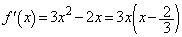 �ł����āA
�ł����āA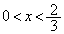 �ɂ�����
�ɂ�����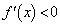 �C
�C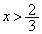 �ɂ�����
�ɂ�����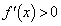 ���A
���A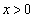 �ɂ����āA
�ɂ����āA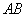 �́A
�́A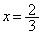 �̂Ƃ��A�ŏ��l
�̂Ƃ��A�ŏ��l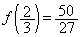 ���Ƃ�܂��B�m���ɁA
���Ƃ�܂��B�m���ɁA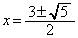 �̂Ƃ�
�̂Ƃ�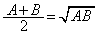 �Ƃ͂Ȃ�܂����A
�Ƃ͂Ȃ�܂����A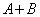 ���ŏ��̂Ƃ�(
���ŏ��̂Ƃ�(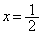 )�ƁA
)�ƁA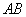 ���ŏ��̂Ƃ�(
���ŏ��̂Ƃ�(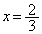 )�Ƃ���v���Ă��܂���B���̏ꍇ�ɂ́A�������ρE���敽�ς̊W��p���čŏ��l�����߂邱�Ƃ͂ł��Ȃ��̂ł��B
)�Ƃ���v���Ă��܂���B���̏ꍇ�ɂ́A�������ρE���敽�ς̊W��p���čŏ��l�����߂邱�Ƃ͂ł��Ȃ��̂ł��B
�����ŁA���嗝�H'11�N[4]�ł́A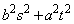 �����l
�����l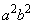 �ƂȂ邱�Ƃɒ��ڂ��āA�������ρE���敽�ς̊W���g���܂����B�~�X���Ղ��|�C���g�Ȃ̂ŁA�悭���ӂ��Ă��������B
�ƂȂ邱�Ƃɒ��ڂ��āA�������ρE���敽�ς̊W���g���܂����B�~�X���Ղ��|�C���g�Ȃ̂ŁA�悭���ӂ��Ă��������B
[5](��������)�@�O���͕��}�ȃx�N�g���̓��όv�Z���s����{���ł����A(4)�͂܂Ƃ��Ɍv�Z���悤�Ƃ���̂ł͑�ςȂ̂ŁA�肪�~�܂邩���m��܂���B������Ɛ������悤�Ƃ���Ɠ���ł����A(3)�̌��ʂ��g���Ē��_C���灢OAB���܂ޕ���H�ɉ��낵�������̑�P���A����AB�Ɋւ��āA��OAB�Ɣ��Α��ɂ��邱�Ƃ��w�E���Ă����悢�ł��傤�B
�x�N�g���̓������Ƃ��Ă͕p�o�^�C�v�̖��ł��B�����������ł����A�����̓w�͂̐��ʂ����āA�������Ő������m�M���������̂ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
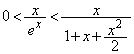 ��
��