���嗝�H���w'11�N[5]
�l�ʑ�OABC�ɂ�����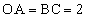 �C
�C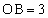 �C
�C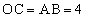 �C
�C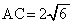 �ł���B�܂��A
�ł���B�܂��A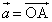 �C
�C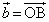 �C
�C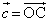 �Ƃ���B�ȉ��̖₢�ɓ�����B
�Ƃ���B�ȉ��̖₢�ɓ�����B
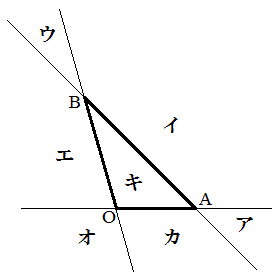 (2) ��OAB���܂ޕ��ʂ�H�Ƃ���BH��̓_P�Œ���PC��H������������̂��Ƃ�B���̂Ƃ��A
(2) ��OAB���܂ޕ��ʂ�H�Ƃ���BH��̓_P�Œ���PC��H������������̂��Ƃ�B���̂Ƃ��A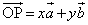 �ƂȂ�x�Cy�����߂�B
�ƂȂ�x�Cy�����߂�B(3) ����H��OA�CAB�CBO�ʼnE�}�̂悤��7�̗̈�A�C�C�C�E�C�G�C�I�C�J�C�L�ɂ킯��B�_P�͂ǂ̗̈�ɓ��邩������B (4) ��AB�Ł�ABC�Ɓ�OAB�̂Ȃ��p�͉s�p�ɂȂ邩�A���p�ɂȂ邩�A����Ƃ��݊p�ɂȂ邩�肹��B�������A1�ӂ����L����2�̎O�p�`�̂Ȃ��p�Ƃ́A���L����ӂɒ������镽�ʂł�2�̎O�p�`�̐���̂Ȃ��p�̂��Ƃł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@1����������邾���Ȃ̂ł����A�������ł͈ӊO�Ƌꂵ�ނ����m��܂���B
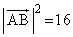 ���A
���A�� 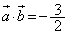 ......[��]
......[��]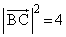 ���A
���A �� 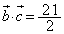 ......[��]
......[��]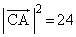 ���A
���A �� 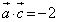 ......[��]
......[��]
(2) 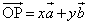 �C
�C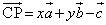
����PC��H����������A�Ƃ������Ƃ́A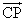 ���AH�����2�̃x�N�g��
���AH�����2�̃x�N�g��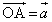 �C
�C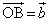 �̂�����Ƃ������ɂȂ�A�Ƃ������Ƃł��B(1)���g���ē��όv�Z�����܂��B
�̂�����Ƃ������ɂȂ�A�Ƃ������Ƃł��B(1)���g���ē��όv�Z�����܂��B
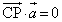 ���A
���A 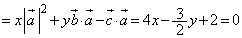 �@����@
�@����@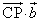 ���A
���A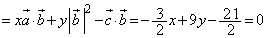 �@����A
�@����A�@�~6�{�A���A
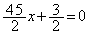 �@��
�@�� 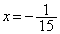 ......[��]
......[��]�A���A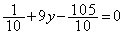 �@��
�@�� 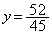 ......[��]
......[��]
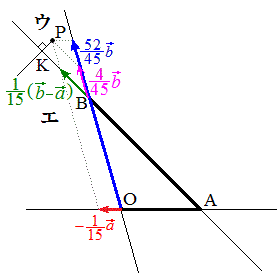 (3) (2)���A
(3) (2)���A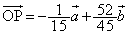 �@����B
�@����B�ƂȂ�܂����A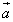 �̌W�������ł��邱�Ƃ���A�_P�͒���OB���������ɂ���܂��B
�̌W�������ł��邱�Ƃ���A�_P�͒���OB���������ɂ���܂��B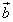 �̌W�������ł��邱�Ƃ���A�_P�͒���OA�����㑤�ɂ���܂��B����āA�_P�̈ʒu�́A�E���G�ł��B�E�ƃG���Ă���̂͒���AB�Ȃ̂ŁA����AB�����E���������邢�͒���AB�ォ�ׂ�悢���ƂɂȂ�܂�(���ʃx�N�g���̉��p���Q��)�B
�̌W�������ł��邱�Ƃ���A�_P�͒���OA�����㑤�ɂ���܂��B����āA�_P�̈ʒu�́A�E���G�ł��B�E�ƃG���Ă���̂͒���AB�Ȃ̂ŁA����AB�����E���������邢�͒���AB�ォ�ׂ�悢���ƂɂȂ�܂�(���ʃx�N�g���̉��p���Q��)�B
�B��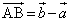 ��
��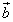 ��1�������ŕ\�����Ƃ��l���܂��B
��1�������ŕ\�����Ƃ��l���܂��B 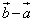 �̌W���A
�̌W���A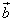 �̌W�����Ƃ��ɐ��Ȃ̂ŁA�_P������̂́A�̈�E ......[��]�NjL�D
�̌W�����Ƃ��ɐ��Ȃ̂ŁA�_P������̂́A�̈�E ......[��]�NjL�D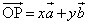 �ƕ\���Ƃ��A
�ƕ\���Ƃ��A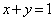 �ł���A�_P�͒���AB��̓_�ł��B
�ł���A�_P�͒���AB��̓_�ł��B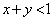 �̂Ƃ��͓_P�͒���AB���O���̓_�ł��B
�̂Ƃ��͓_P�͒���AB���O���̓_�ł��B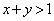 �̂Ƃ��͓_P�͒���AB�Ɋւ���O�Ɣ��Α��̓_�ł��B�B�ł́A
�̂Ƃ��͓_P�͒���AB�Ɋւ���O�Ɣ��Α��̓_�ł��B�B�ł́A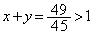 �Ȃ̂ŁA����������A�_P���̈�E�ɂ��邱�Ƃ��킩��܂��B
�Ȃ̂ŁA����������A�_P���̈�E�ɂ��邱�Ƃ��킩��܂��B
(4) P���璼��AB�ɐ���PK�����낵�A��OAB���܂ޕ��ʓ��œ_K��ʂ�x�N�g���ƁA��ABC���܂ޕ��ʓ��œ_K��ʂ�x�N�g���Ƃ̓��ς̐������l����悢(2�O�p�`�̂Ȃ��p�́A���ς����Ȃ�s�p�A0�Ȃ璼�p�A���Ȃ�݊p)�̂ł����A���ς̌v�Z�͕��G�ł��B�����ł́A(3)�𗘗p���܂��B
2�̎O�p�`�����L�����AB�ɒ������镽�ʂƂ��āA�_K��ʂ蒼��AB�ɐ����ȕ���α���l����ƁA�O�p�`OAB���܂ޕ��ʂƕ���α�Ƃ̌���́A�_K�Œ���AB�ƒ������܂��B�O�p�`ABC���܂ޕ��ʂƕ���α�Ƃ̌���͒���CK�ł��B����CK�́A����AB�ƒ������܂��B�_C���灢OAB���܂ޕ���H�ɉ��낵���_���_P�ŁA�_P�́A����AB�̉E���A��OAB�͕�AB�������Ē���AB�̍����ɂ���̂ŁA��ABC�Ɓ�OAB�̂Ȃ��p�͓݊p ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B