�эL�{�Y�吔�w'08�N[2]
���_��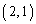 �ŁA�_
�ŁA�_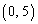 ��ʂ�2����
��ʂ�2����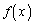 ������A
������A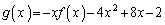 �Ƃ���B
�Ƃ���B
(1) ��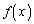 �����߂�B
�����߂�B (2) 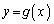 �̑����\�����A���̃O���t�������B
�̑����\�����A���̃O���t�������B (3) �Ȑ�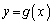 ��
��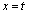 �ɂ�����ڐ��̕����������߂�B
�ɂ�����ڐ��̕����������߂�B (4) �Ȑ�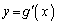 ��x���Ƃň͂܂ꂽ�����ŁA��ӂ�x���ƕ��s�ł���2�̒��_���Ȑ�
��x���Ƃň͂܂ꂽ�����ŁA��ӂ�x���ƕ��s�ł���2�̒��_���Ȑ�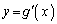 ��ɂ��钷���`�����Ƃ��A�ʐς��ő�ƂȂ钷���`��4�̒��_�̍��W�Ƃ��̖ʐς����߂�B
��ɂ��钷���`�����Ƃ��A�ʐς��ő�ƂȂ钷���`��4�̒��_�̍��W�Ƃ��̖ʐς����߂�B (5) �_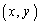 ����Ȑ�
����Ȑ�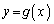 �ɈقȂ�3�{�̐ڐ���������Ƃ��A�_
�ɈقȂ�3�{�̐ڐ���������Ƃ��A�_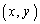 �̑��݂���͈͂�s�����ŕ\���A�܂����͈̔͂�}������B
�̑��݂���͈͂�s�����ŕ\���A�܂����͈̔͂�}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@2�����A3�����̃O���t����A�ڐ�����A�ő�l����A2���������A3���������̉��̏�������A���ݔ͈͂���A�ŁA�Ă���̃Z���^�[�����p���K���ł��B
(1) 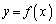 �̒��_��
�̒��_��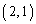 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A 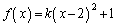 �Ƃ������Ƃ��ł��܂�(2�������Q��)�B
�Ƃ������Ƃ��ł��܂�(2�������Q��)�B
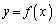 ��
��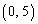 ��ʂ�̂ŁA
��ʂ�̂ŁA�� 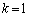 ��
�� 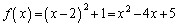 ......[��]
......[��]
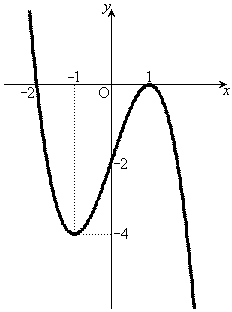 (2)
(2) 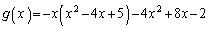
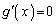 �Ƃ���ƁA
�Ƃ���ƁA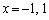
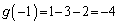 �C
�C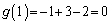
(3) �Ȑ�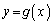 ��
��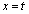 �ɂ������ڐ��́A
�ɂ������ڐ��́A �������āA
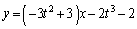 ......[��]�@����@
......[��]�@����@
(4) �Ȑ�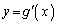 ��y���Ɋւ��đΏ̂Ȃ̂ŁA�����`���Ώ̂ɂȂ�Ax���ƕ��s�ȕӂ̗��[�ɂ���Ȑ�
��y���Ɋւ��đΏ̂Ȃ̂ŁA�����`���Ώ̂ɂȂ�Ax���ƕ��s�ȕӂ̗��[�ɂ���Ȑ�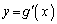 ���2�_�́A
���2�_�́A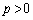 �Ƃ��āA
�Ƃ��āA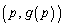 �C
�C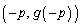 (
(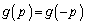 )�ł��B�������A����2�_�́A�Ȑ�
)�ł��B�������A����2�_�́A�Ȑ�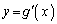 ��
��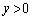 �̕����ɑ��݂���̂ŁA
�̕����ɑ��݂���̂ŁA ���A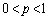 �ł��B
�ł��B
�����`�̉���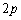 �C�c��
�C�c��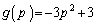 ���A�����`�̖ʐ�
���A�����`�̖ʐ�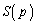 �́A
�́A �����\���A�����`�̖ʐς�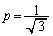 �̂Ƃ��ő�l
�̂Ƃ��ő�l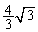 ......[��]�@���Ƃ�(3�����̍ő�E�ŏ����Q��)�A
......[��]�@���Ƃ�(3�����̍ő�E�ŏ����Q��)�A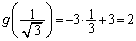 ���A���̂Ƃ��A�����`��4���_�̍��W�́A
���A���̂Ƃ��A�����`��4���_�̍��W�́A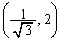 �C
�C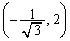 �C
�C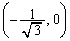 �C
�C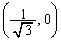 ......[��]
......[��]
(5) �_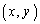 ����Ȑ�
����Ȑ�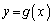 �ɈقȂ�3�{�̐ڐ���������Ƃ��A���̓_��x���W��a�Cy���W��b���������Ƃɂ��܂�(x�Cy�̂܂܂��ƁA�Ȑ�
�ɈقȂ�3�{�̐ڐ���������Ƃ��A���̓_��x���W��a�Cy���W��b���������Ƃɂ��܂�(x�Cy�̂܂܂��ƁA�Ȑ�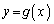 ��̓_�A�ڐ���̓_�ƍ������₷���Ȃ�̂ŁA�ʂ̕����ɂ��܂�)�B�ڐ��@���_
��̓_�A�ڐ���̓_�ƍ������₷���Ȃ�̂ŁA�ʂ̕����ɂ��܂�)�B�ڐ��@���_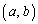 ��ʂ�̂ŁA
��ʂ�̂ŁA �����t�Ɋւ���3���������ƌ��Đ�������ƁA
���̍��ӂ�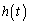 �Ƃ����ƁA�_
�Ƃ����ƁA�_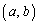 ����Ȑ�
����Ȑ�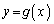 ��3�{�̐ڐ���������A�Ƃ������Ƃ́A�ړ_��3�ł��āA�ړ_��x���W�����ɂ���3��������
��3�{�̐ڐ���������A�Ƃ������Ƃ́A�ړ_��3�ł��āA�ړ_��x���W�����ɂ���3��������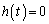 �����قȂ�3�����������A�Ƃ������Ƃł��B
�����قȂ�3�����������A�Ƃ������Ƃł��B
���̂��߂̏����́A��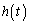 ���ɑ�Ƌɏ��������A(�ɑ�l)�~(�ɏ��l)�����ɂȂ邱�Ƃł�(�����@�̕������ւ̉��p���Q��)�B
���ɑ�Ƌɏ��������A(�ɑ�l)�~(�ɏ��l)�����ɂȂ邱�Ƃł�(�����@�̕������ւ̉��p���Q��)�B 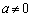 �ł���A�ɑ�A�ɏ������݂��܂�(2��������
�ł���A�ɑ�A�ɏ������݂��܂�(2��������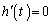 �̔��ʎ������A�Ƃ��Ă�OK)�B
�̔��ʎ������A�Ƃ��Ă�OK)�B
���̂Ƃ��A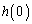 �C
�C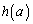 �̂����ꂩ������ɑ�l�ő������ɏ��l�ł��B����āA
�̂����ꂩ������ɑ�l�ő������ɏ��l�ł��B����āA�����ŁA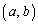 ��
��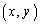 �ɖ߂��ƁA�_
�ɖ߂��ƁA�_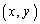 ����Ȑ�
����Ȑ�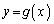 �ɈقȂ�3�{�̐ڐ�������������́A
�ɈقȂ�3�{�̐ڐ�������������́A �ƂȂ�܂����A�s�����ɂ�����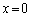 �Ƃ��Ă��A
�Ƃ��Ă��A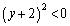 �ƂȂ��Đ��藧���Ȃ��̂ŁA�_
�ƂȂ��Đ��藧���Ȃ��̂ŁA�_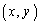 �̑��݂���͈͂́A
�̑��݂���͈͂́A 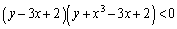 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B