���嗝�H���w'11�N[4]
xy-���ʏ�̌��_��O�Ƃ��A�ȉ~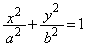 (
(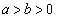 )��E�Ƃ���BE��̓_P
)��E�Ƃ���BE��̓_P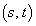 �ɂ�����E�̖@����x���Ƃ̌�_��Q�Ƃ���B�_P��
�ɂ�����E�̖@����x���Ƃ̌�_��Q�Ƃ���B�_P��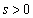 �C
�C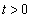 �͈̔͂��Ƃ��A
�͈̔͂��Ƃ��A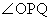 ���ő�ɂȂ�_P�����߂�B
���ő�ɂȂ�_P�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@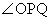 �͒���OP�Ɩ@���̂Ȃ��p�Ȃ̂ŁA�����̌X�����琳�ڂ̉��@�藝���l���邱�ƂɂȂ�܂��B
�͒���OP�Ɩ@���̂Ȃ��p�Ȃ̂ŁA�����̌X�����琳�ڂ̉��@�藝���l���邱�ƂɂȂ�܂��B
P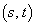 ���ȉ~��̓_�Ȃ̂ŁA
���ȉ~��̓_�Ȃ̂ŁA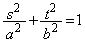
����āA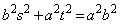 �@����@
�@����@
P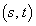 �ɂ�����E�̐ڐ��́A
�ɂ�����E�̐ڐ��́A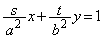
���̌X����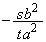 �C����āA�@����x���������Ƃ̂Ȃ��p��α�Ƃ��āA�@���̌X����
�C����āA�@����x���������Ƃ̂Ȃ��p��α�Ƃ��āA�@���̌X����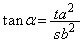 �ł�(2�����̕��s�E�������Q��)�B
�ł�(2�����̕��s�E�������Q��)�B
����OP��x���������Ƃ̂Ȃ��p��β �Ƃ��āA����OP�̌X����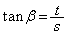
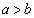 �Ȃ̂ŁA�@����x���Ƃ̌�_Q��
�Ȃ̂ŁA�@����x���Ƃ̌�_Q��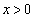 �̕����ɂ��邱�Ƃ���A
�̕����ɂ��邱�Ƃ���A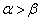
����āA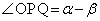
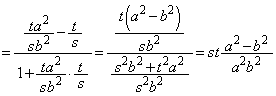 �@(�� �@)
�@(�� �@)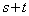 �͈��l�ł͂Ȃ��̂ŁA�������ϑ��敽�ς̊W��
�͈��l�ł͂Ȃ��̂ŁA�������ϑ��敽�ς̊W��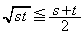 �̌`�ł͎g�����Ƃ͂ł��܂��A�@�̉E��
�̌`�ł͎g�����Ƃ͂ł��܂��A�@�̉E��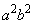 �����ł��邱�Ƃɒ��ڂ��āA�������ϑ��敽�ς̊W���A
�����ł��邱�Ƃɒ��ڂ��āA�������ϑ��敽�ς̊W���A
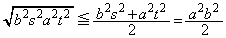 (�s�����̓�������������̂�
(�s�����̓�������������̂�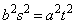 �C�܂�A
�C�܂�A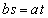 �̂Ƃ�)
�̂Ƃ�)
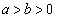 �C
�C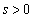 �C
�C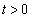 ���A
���A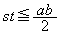
�� 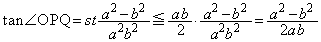
�s�����̓�������������̂́A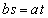 �̂Ƃ��ŁA���̂Ƃ��A�@���A
�̂Ƃ��ŁA���̂Ƃ��A�@���A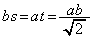 �C
�C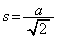 �C
�C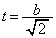
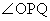 ���ő�ƂȂ�_P�́A
���ő�ƂȂ�_P�́A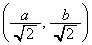 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 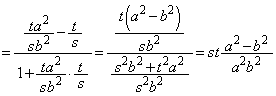 �@(�� �@)
�@(�� �@)