���嗝�H���w'11�N[1]
xy-���ʏ�̕�����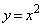 ��C�Ƃ���B�ȉ��̖₢�ɓ�����B
��C�Ƃ���B�ȉ��̖₢�ɓ�����B
(1) C��̓_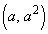 �ɂ�����C�̖@���̕����������߂�B
�ɂ�����C�̖@���̕����������߂�B (2) �_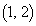 ��ʂ�@���̐������߂�B
��ʂ�@���̐������߂�B (3) �_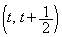 ��ʂ�C�̖@���̐���2�ƂȂ邽�߂�t �ɑ�����������߂�B
��ʂ�C�̖@���̐���2�ƂȂ邽�߂�t �ɑ�����������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(3)�ł́A���ǁA3�����̋ɒl�ׂ邱�ƂɂȂ�܂��B
(1) C�F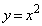
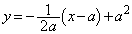
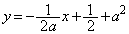 ......[��]�@����@
......[��]�@����@
(2) �@���_ ��ʂ�̂ŁA
��ʂ�̂ŁA �� 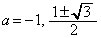
a��3�ʂ�̒l��3�{�̈قȂ�@����^���܂��B����āA�_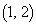 ��ʂ�@���̐��́A3 ......[��]
��ʂ�@���̐��́A3 ......[��]
(3) �@���_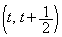 ��ʂ�̂ŁA
��ʂ�̂ŁA 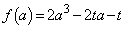 �Ƃ����ƁA
�Ƃ����ƁA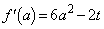
�@���̐���2�ƂȂ邽�߂ɁA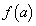 �͋ɑ�A�ɏ������K�v������(3�����̑������Q��)�A2��������
�͋ɑ�A�ɏ������K�v������(3�����̑������Q��)�A2��������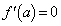 �͑��قȂ�2�������������܂��B����āA
�͑��قȂ�2�������������܂��B����āA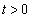 ���K�v�ŁA
���K�v�ŁA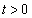 �̂��ƂɁA
�̂��ƂɁA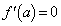 �́A2��
�́A2��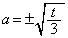 �������܂��B
�������܂��B
���̂Ƃ��A�@���̐���2�ƂȂ邽�߂ɁA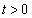 �̂��Ƃŋɑ�l���邢�͋ɏ��l��0�ƂȂ邱�Ƃ��K�v�\���ŁA
�̂��Ƃŋɑ�l���邢�͋ɏ��l��0�ƂȂ邱�Ƃ��K�v�\���ŁA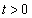 ���A
���A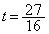 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B