早大理工数学'11年[3]
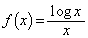 とする。以下の問いに答えよ。
とする。以下の問いに答えよ。
(1) 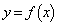 のグラフの概形を次の点に注意して描け:
のグラフの概形を次の点に注意して描け: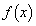 の増減、グラフの凹凸、
の増減、グラフの凹凸、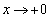 ,
,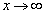 のときの
のときの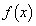 の挙動。
の挙動。 (2) nを自然数とする。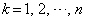 に対してxが
に対してxが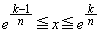 を動くときの
を動くときの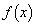 の最大値を
の最大値を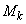 ,最小値を
,最小値を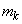 とし、
とし、 とおく。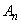 ,
,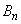 を求めよ。
を求めよ。 (3) 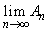 および
および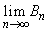 を求めよ。
を求めよ。 (4) 各nに対して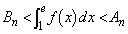 であることを示せ。
であることを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 極限と微分に関する基本問題です。こうした問題で着実に得点できるように、基本反復演習をしておいて欲しいというのが出題者の意図でしょう。
なお、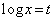 とおいて置換成分することにより、
とおいて置換成分することにより、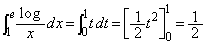 なので、(3)の結果は最初から見えています。
なので、(3)の結果は最初から見えています。
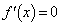 とすると、
とすると、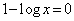 ∴
∴ 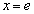 ,このとき、
,このとき、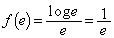
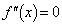 とすると、
とすると、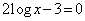 ∴
∴ 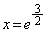 ,このとき、
,このとき、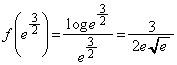
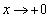 のとき、
のとき、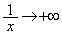 ,
,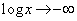 より、
より、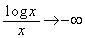
これより、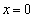 (y軸)が漸近線になります。
(y軸)が漸近線になります。
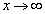 のときの
のときの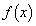 の挙動を調べるために準備をします。
の挙動を調べるために準備をします。
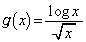 とおくと、
とおくと、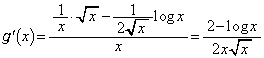
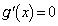 とすると、
とすると、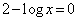 ∴
∴ 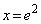 ,このとき、
,このとき、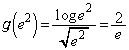 増減表より、
増減表より、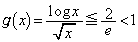 (関数の増減を参照)
(関数の増減を参照)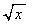 で割ると、
で割ると、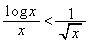
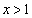 において
において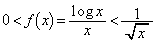
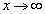 のとき、
のとき、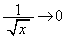 ,はさみうちの原理より、
,はさみうちの原理より、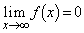
また、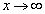 のとき、
のとき、 ,これより、
,これより、 (x軸)が漸近線になります。
(x軸)が漸近線になります。
 の増減表は以下のようになります。
の増減表は以下のようになります。 以上より、
以上より、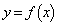 のグラフは右図太線。
のグラフは右図太線。
(2) 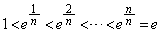 より、
より、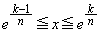 (
(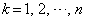 )において、
)において、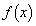 は単調増加です。この範囲における
は単調増加です。この範囲における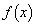 の最大値
の最大値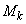 ,最小値
,最小値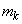 は、
は、 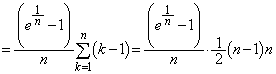
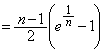 ......[答]
......[答]
(3) 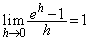 (極限の公式を参照)を利用するために、(2)の結果で、
(極限の公式を参照)を利用するために、(2)の結果で、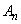 を
を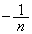 で割って
で割って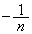 をかけます。
をかけます。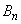 を
を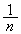 で割って
で割って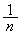 をかけます。
をかけます。 ∴ 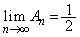 ,
,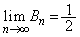 ......[答]
......[答]
(4) 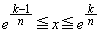 において,
において,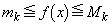
範囲内で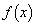 は、恒等的に
は、恒等的に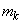 ,あるいは
,あるいは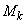 に等しい、ということはないので、
に等しい、ということはないので、 各辺を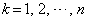 について加え合わせると、
について加え合わせると、 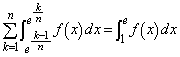 より、
より、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 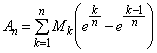
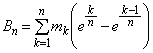
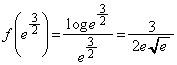
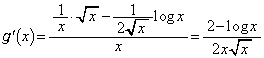
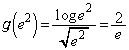
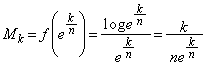
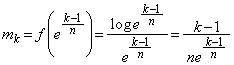
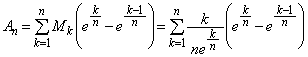
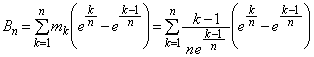
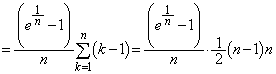
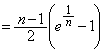 ......[答]
......[答]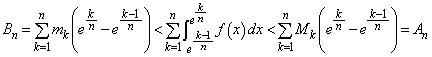
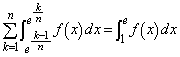 より、
より、