極限 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
極限は、微分・積分を考える上での基礎概念です。正確な議論をしようとすると、大学入試のレベルを超えてしまうので、ここでは、
‘nを限りなく大きくすると(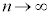 と表す)'、数列の第n項
と表す)'、数列の第n項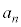 はどうなるか(これを数列の極限と言い、
はどうなるか(これを数列の極限と言い、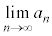 と表す)、また、‘xを限りなく大きくすると(
と表す)、また、‘xを限りなく大きくすると(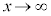 と表す)'、‘xを限りなくaに近づけると(
と表す)'、‘xを限りなくaに近づけると(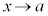 と表す)'、関数
と表す)'、関数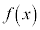 はどうなるか(これを関数
はどうなるか(これを関数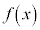 の極限と言い、
の極限と言い、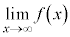 ,
,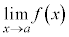 などと表す)、といった表現で理解することにします。
などと表す)、といった表現で理解することにします。
ここで学習する内容は、以下の通りです。各項目をクリックしてください。
数列の極限 数列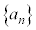 において、
において、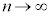 のとき、数列の第n項
のとき、数列の第n項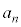 の動きを考えます。
の動きを考えます。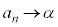 となるならαを極限値と言い、数列
となるならαを極限値と言い、数列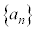 はαに収束すると言います。
はαに収束すると言います。
等比数列の極限 等比数列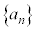 が0に収束する条件は、公比rについて、
が0に収束する条件は、公比rについて、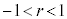
無限級数 数列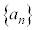 の各項の和を無限にとったもの
の各項の和を無限にとったもの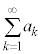 を無限級数と言います。部分和
を無限級数と言います。部分和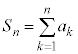 が、
が、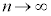 のとき
のとき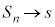 となるなら、sを無限級数の和と言います。
となるなら、sを無限級数の和と言います。
無限等比級数 初項a,公比rの等比数列の各項の和を無限にとった無限等比級数が収束する条件は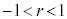 ,このときの和は
,このときの和は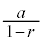
関数の極限 関数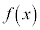 において、
において、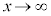 のとき、
のとき、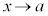 のときの、関数の動きを考えます。
のときの、関数の動きを考えます。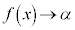 となるならαを極限値と言います。
となるならαを極限値と言います。
不定形の極限 単純に、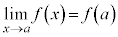 としたのでは求められない極限を求める技巧を学びます。
としたのでは求められない極限を求める技巧を学びます。
はさみうちの原理 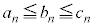 ,
,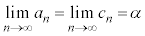 であれば、
であれば、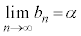 です。また、
です。また、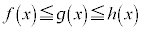 ,
,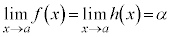 であれば、
であれば、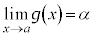 です。
です。
極限の公式 公式: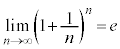 ,
,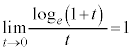 ,
,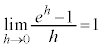 ,
,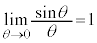 は、微分法において導関数を求める基礎となる公式です。
は、微分法において導関数を求める基礎となる公式です。
関数の連続 関数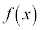 が
が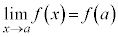 を満たすとき、
を満たすとき、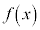 は
は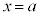 において連続です。
において連続です。
最大値・最小値の定理 閉区間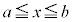 において連続な関数
において連続な関数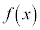 は、最大値、最小値をもちます。
は、最大値、最小値をもちます。
中間値の定理 閉区間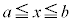 において連続な関数
において連続な関数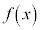 について、
について、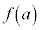 と
と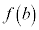 の間の値をとるところが必ずある、という定理です。
の間の値をとるところが必ずある、という定理です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 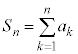 が、
が、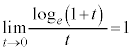 ,
,