早大理工数学'13年[4]
 半径1の半円を底面とし、高さが1の半円柱に含まれる立体Rがある。その高さx (
半径1の半円を底面とし、高さが1の半円柱に含まれる立体Rがある。その高さx (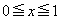 )での断面が、次の図のように2つの直角三角形を合わせた形になっている。次の問いに答えよ。
)での断面が、次の図のように2つの直角三角形を合わせた形になっている。次の問いに答えよ。
(1) 高さxでのRの断面積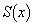 を求めよ。
を求めよ。 (2) Rの体積を求めよ。必要ならば、積分する際に と置き換えよ。
と置き換えよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (1)では立体の形状を追求しないのがコツです。断面積を積分するだけで、早大理工としては、物足りない感じがします。
 (1) 右図において、△ABC∽△ACFより、AB:AC=AC:AF
(1) 右図において、△ABC∽△ACFより、AB:AC=AC:AF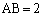 ,
,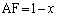 より、
より、
三平方の定理より、
また、EO//CFより、BO:BC=EO:CF∴ 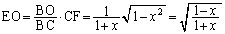
 ......[答]
......[答]
(2) Rの体積Vは、 より、
より、 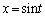 とおくと、
とおくと、 ,
,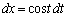 ,x:
,x: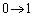 のとき、t:
のとき、t: (置換積分を参照)
(置換積分を参照)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 