早稲田大学基幹・創造・先進理工学部2013年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 放物線C: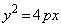 (
(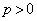 )の焦点F
)の焦点F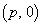 を通る2直線
を通る2直線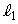 ,
,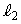 は互いに直交し、Cと
は互いに直交し、Cと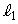 は2点
は2点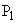 ,
,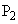 で、Cと
で、Cと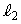 は2点
は2点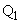 ,
,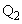 で交わるとする。次の問いに答えよ。
で交わるとする。次の問いに答えよ。
(1) 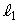 の方程式を
の方程式を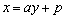 と置き、
と置き、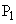 ,
,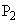 の座標をそれぞれ
の座標をそれぞれ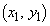 ,
,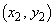 とする。
とする。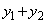 ,
,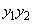 をaとpで表せ。
をaとpで表せ。 (2) 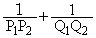 は
は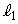 ,
,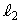 のとり方によらず一定であることを示せ。
のとり方によらず一定であることを示せ。 [解答へ]
[2] 複素数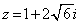 と自然数
と自然数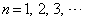 について、複素数
について、複素数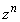 を実数
を実数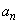 ,
,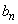 を用いて
を用いて
と表す。次の問いに答えよ。
(1) 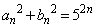 (
(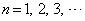 )であることを示せ。
)であることを示せ。 (2) すべてのnについて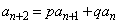 が成り立つ定数p,qを求めよ。
が成り立つ定数p,qを求めよ。 (3) どんなnについても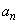 は5の整数倍でないことを示せ。
は5の整数倍でないことを示せ。 (4) 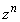 (
(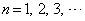 )は実数でないことを示せ。
)は実数でないことを示せ。 [解答へ]
[3] 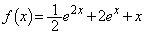 とする。次の問いに答えよ。
とする。次の問いに答えよ。
(1) 実数t に対して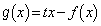 とおく。xが実数全体を動くとき、
とおく。xが実数全体を動くとき、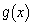 が最大値をもつようなt の範囲を求めよ。またt がその範囲にあるとき、
が最大値をもつようなt の範囲を求めよ。またt がその範囲にあるとき、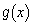 の最大値とそのときのxの値を求めよ。
の最大値とそのときのxの値を求めよ。 (2) (1)で求めた最大値を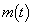 とする。aを定数とし、t の関数
とする。aを定数とし、t の関数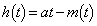 を考える。t が(1)で求めた範囲を動くとき、
を考える。t が(1)で求めた範囲を動くとき、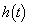 の最大値を求めよ。
の最大値を求めよ。 [解答へ]
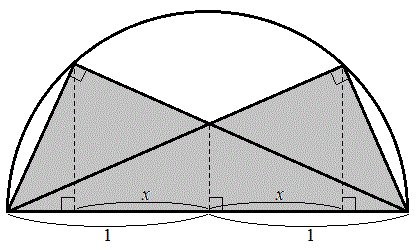 [4] 半径1の半円を底面とし、高さが1の半円柱に含まれる立体Rがある。その高さx (
[4] 半径1の半円を底面とし、高さが1の半円柱に含まれる立体Rがある。その高さx (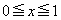 )での断面が、次の図のように2つの直角三角形を合わせた形になっている。次の問いに答えよ。
)での断面が、次の図のように2つの直角三角形を合わせた形になっている。次の問いに答えよ。
(1) 高さxでのRの断面積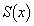 を求めよ。
を求めよ。 (2) Rの体積を求めよ。必要ならば、積分する際に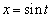 と置き換えよ。
と置き換えよ。 [解答へ]
[5] 空間内に平面Pがある。空間内の図形Aに対し、Aの各点からPに下ろした垂線とPとの交点の全体を、AのPへの正射影と呼ぶ。次の問いに答えよ。
(1) 平面Qが平面Pと角θ (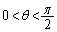 )で交わっているとする。すなわち、PとQの交線に垂直な平面でP,Qを切ってできる2直線のなす角がθ であるとする。Q上の長さ1の線分のPへの正射影の長さの最大値と最小値を求めよ。
)で交わっているとする。すなわち、PとQの交線に垂直な平面でP,Qを切ってできる2直線のなす角がθ であるとする。Q上の長さ1の線分のPへの正射影の長さの最大値と最小値を求めよ。 (2) (1)のQを考える。Q上の1辺の長さが1である正三角形のPへの正射影の面積を求めよ。
(3) 1辺の長さが1である正四面体TのPへの正射影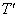 はどんな形か。また、
はどんな形か。また、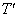 の面積の最大値を求めよ。
の面積の最大値を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。