���嗝�H���w'13�N[2]
���f��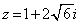 �Ǝ��R��
�Ǝ��R��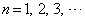 �ɂ��āA���f��
�ɂ��āA���f��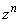 ������
������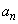 �C
�C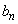 ��p����
��p����
�ƕ\���B���̖₢�ɓ�����B
(1) 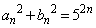 (
(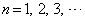 )�ł��邱�Ƃ������B
)�ł��邱�Ƃ������B (2) ���ׂĂ�n�ɂ���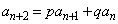 �����藧�萔p�Cq�����߂�B
�����藧�萔p�Cq�����߂�B (3) �ǂ��n�ɂ��Ă�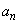 ��5�̐����{�łȂ����Ƃ������B
��5�̐����{�łȂ����Ƃ������B (4) 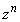 (
(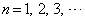 )�͎����łȂ����Ƃ������B
)�͎����łȂ����Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�A���Q�����̖��ł��B(3)�ł�(2)���A(4)�ł�(1)�C(3)���A�q���g�ɂȂ��Ă��邱�ƂɋC�Â��K�v������܂�
(1) 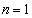 �̂Ƃ��A
�̂Ƃ��A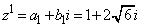 ���A
���A 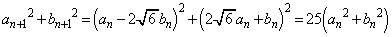 (
(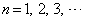 )
)������J��Ԃ��p���āA
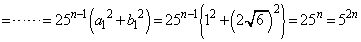 (
(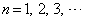 )�@(�� �@)
)�@(�� �@)
(2) �A���A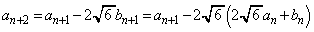
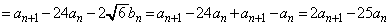 �@����B
�@����B����āA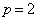 �C
�C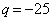 ......[��]
......[��]
�@�C�A���A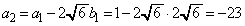
�B���A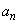 �C
�C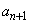 �������Ȃ�
�������Ȃ� �������Ȃ̂ŁA�A�[�I�ɂ��ׂĂ̎��R��n�ɂ��āA
�������Ȃ̂ŁA�A�[�I�ɂ��ׂĂ̎��R��n�ɂ��āA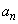 �͐����ł�(���w�I�A�[�@���Q��)�B�܂��A
�͐����ł�(���w�I�A�[�@���Q��)�B�܂��A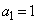 �C
�C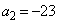 ��5�̔{���ł͂���܂���B
��5�̔{���ł͂���܂���B
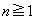 �̂Ƃ��A
�̂Ƃ��A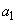 �C
�C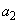 �C����C
�C����C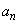 �C
�C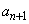 �̂��ׂĂ�5�̔{���łȂ��A
�̂��ׂĂ�5�̔{���łȂ��A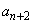 ��5�̔{���Ɖ��肵�܂��Bk�𐮐��Ƃ��āA
��5�̔{���Ɖ��肵�܂��Bk�𐮐��Ƃ��āA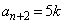 �Ƃ������Ƃ��ł��܂��B
�Ƃ������Ƃ��ł��܂��B
�B���A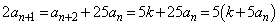
������A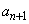 ��5�̔{���ƂȂ�A����Ɩ������܂��B����āA
��5�̔{���ƂȂ�A����Ɩ������܂��B����āA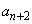 ��5�̔{���Ƃ�������͌��ŁA
��5�̔{���Ƃ�������͌��ŁA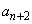 ��5�̔{���ł͂���܂���B
��5�̔{���ł͂���܂���B
�]���āA���ׂĂ̎��R��n�ɂ��āA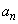 ��5�̔{���ł͂���܂���B
��5�̔{���ł͂���܂���B
(4) �w���@��p���ďؖ����܂��B
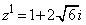 �͎����ł͂���܂���(���f�����Q��)�B
�͎����ł͂���܂���(���f�����Q��)�B
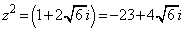 �������ł͂���܂���B
�������ł͂���܂���B
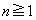 �̂Ƃ��A
�̂Ƃ��A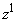 �C
�C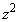 �C����C
�C����C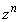 �C
�C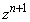 �̂��ׂĂ������łȂ��A
�̂��ׂĂ������łȂ��A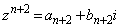 �������A�܂�A
�������A�܂�A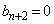 �Ɖ��肵�܂��B(1)���A
�Ɖ��肵�܂��B(1)���A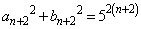 �ł����A
�ł����A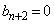 �̂Ƃ��A
�̂Ƃ��A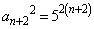 �C�܂�A
�C�܂�A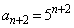 �ƂȂ�A(3)�̌��ʂƖ������܂��B����āA
�ƂȂ�A(3)�̌��ʂƖ������܂��B����āA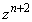 �������Ƃ�������͌��ŁA
�������Ƃ�������͌��ŁA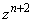 �͎����ł͂���܂���B
�͎����ł͂���܂���B
�]���āA���ׂĂ̎��R��n�ɂ��āA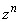 �͎����ł͂���܂���B
�͎����ł͂���܂���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B