早大理工数学'13年[5]
空間内に平面Pがある。空間内の図形Aに対し、Aの各点からPに下ろした垂線とPとの交点の全体を、AのPへの正射影と呼ぶ。次の問いに答えよ。
(1) 平面Qが平面Pと角θ (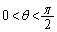 )で交わっているとする。すなわち、PとQの交線に垂直な平面でP,Qを切ってできる2直線のなす角がθ であるとする。Q上の長さ1の線分のPへの正射影の長さの最大値と最小値を求めよ。
)で交わっているとする。すなわち、PとQの交線に垂直な平面でP,Qを切ってできる2直線のなす角がθ であるとする。Q上の長さ1の線分のPへの正射影の長さの最大値と最小値を求めよ。 (2) (1)のQを考える。Q上の1辺の長さが1である正三角形のPへの正射影の面積を求めよ。
(3) 1辺の長さが1である正四面体TのPへの正射影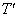 はどんな形か。また、
はどんな形か。また、 の面積の最大値を求めよ。
の面積の最大値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 本問はヒントがついていますが、物議を醸した東大理系'88年[2]の再来か、という問題です。(3)は早大理工11年[5](3)を参照してください。
(1) 平面Pと平面Qの交線を とします。Q上の長さ1の線分の端点のうちの片方が
とします。Q上の長さ1の線分の端点のうちの片方が 上に来るように線分を平行移動させても一般性を失いません。
上に来るように線分を平行移動させても一般性を失いません。 上に来た端点をA,長さ1の線分の他方の端点をBとします。
上に来た端点をA,長さ1の線分の他方の端点をBとします。 Q上で、ABと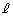 のなす角をφ (
のなす角をφ ( )とします。Bから
)とします。Bから に垂線BHを下ろすと、
に垂線BHを下ろすと、 ,Bから平面Pに垂線BKを下ろすと、
,Bから平面Pに垂線BKを下ろすと、 です(三角比を参照)。ABの正射影AKの長さは、三平方の定理より、
です(三角比を参照)。ABの正射影AKの長さは、三平方の定理より、  より、AKの長さは、
より、AKの長さは、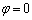 のときに最大値1,
のときに最大値1, のときに最小値
のときに最小値 ......[答] をとります。
......[答] をとります。
(2) 1辺の長さが1の正三角形の1頂点が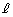 上に来るように正三角形を平行移動させても一般性を失いません。
上に来るように正三角形を平行移動させても一般性を失いません。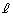 に来た頂点をA,他の2頂点をB,Cとし、辺AB,辺ACと
に来た頂点をA,他の2頂点をB,Cとし、辺AB,辺ACと がなす角をα,β とします。αとβと
がなす角をα,β とします。αとβと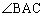 に重なりができないようにα,β をとれば、
に重なりができないようにα,β をとれば、 より、
より、 です。
です。 Bから ,平面Pに垂線BH,BKを下ろし、Cから
,平面Pに垂線BH,BKを下ろし、Cから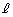 ,平面Pに垂線CL,CMを下ろすと、(1)と同様にして、
,平面Pに垂線CL,CMを下ろすと、(1)と同様にして、 Bを通って に平行な直線と辺ACとの交点をJとし、Jから平面Pに垂線JNを下ろすと、KN // BJ //
に平行な直線と辺ACとの交点をJとし、Jから平面Pに垂線JNを下ろすと、KN // BJ // です。正弦定理より、
です。正弦定理より、 ∴  正三角形ABCの正射影の面積は、
正三角形ABCの正射影の面積は、 
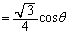 ......[答]
......[答]別解.直線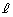 に垂直な平面で切って考えることもできます。
に垂直な平面で切って考えることもできます。 直線 に沿ってx軸をとり、x座標がxのところを通る平面(x軸に垂直)で、1辺の長さ1の正三角形を切ったときの切り口にできる線分の長さを
に沿ってx軸をとり、x座標がxのところを通る平面(x軸に垂直)で、1辺の長さ1の正三角形を切ったときの切り口にできる線分の長さを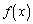 とすると、正三角形の存在範囲が
とすると、正三角形の存在範囲が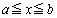 だとして、正三角形の面積は、
だとして、正三角形の面積は、 となります。(1)より、この線分の正射影の長さは となるので、正三角形の正射影の面積は、
となるので、正三角形の正射影の面積は、
(3) 正四面体Tの4頂点をO,A,B,Cとし、三角形ABCが存在する面を平面Qとします。
Oから平面Pに垂線OHを下ろすとき、直線OHが三角形ABCの周上または内部を通過する場合と通過しない場合があります。
(i) 直線OHが三角形ABCの周上または内部を通過する場合
三角形ABCの正射影を三角形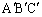 として、Hは三角形
として、Hは三角形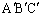 の周上または内部の点です。
の周上または内部の点です。
従って、正四面体Tの正射影 は三角形
は三角形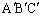 となります。
となります。
このときは、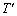 の面積は、(2)より、
の面積は、(2)より、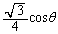 となります。
となります。
 より、
より、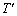 の面積の最大値は
の面積の最大値は です。
です。 (ii) 直線OHが三角形ABCの周上または内部を通過しない場合
このとき、Hは三角形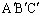 の外部の点です。外部の点と言っても、直線
の外部の点です。外部の点と言っても、直線 と直線
と直線 に挟まれていて、辺
に挟まれていて、辺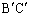 を介して三角形
を介して三角形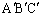 と隣接している領域、三角形
と隣接している領域、三角形 と頂点
と頂点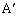 のみを共有している領域など、全部で6つの領域に分かれます。
のみを共有している領域など、全部で6つの領域に分かれます。 (a) Hが、三角形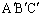 と頂点
と頂点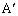 のみを共有している領域にある(半直線
のみを共有している領域にある(半直線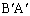 上で線分
上で線分 上を除く部分にある場合、半直線
上を除く部分にある場合、半直線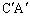 上で線分
上で線分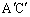 上を除く部分にある場合を含む)場合は、
上を除く部分にある場合を含む)場合は、 は正三角形OBCの正射影に一致し、正射影の形は三角形です。この場合の
は正三角形OBCの正射影に一致し、正射影の形は三角形です。この場合の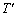 の面積の最大値は(i)と同じく
の面積の最大値は(i)と同じく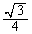 です。
です。 Hが、頂点 のみ、あるいは、頂点
のみ、あるいは、頂点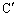 のみを共有している領域にある場合も同様です。
のみを共有している領域にある場合も同様です。 (b) Hが、半直線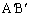 と半直線
と半直線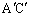 に挟まれていて、辺
に挟まれていて、辺 を介して三角形
を介して三角形 と隣接している領域にある(境界線上は除きます)場合、正射影の形は四角形
と隣接している領域にある(境界線上は除きます)場合、正射影の形は四角形 になります。
になります。 三角形ABC(平面Q)と平面Pのなす角は、BCの中点をMとして、三角形ABCと平面PをAMを含む平面で切断したときに切り口にできる角です。これをθ とします。直線AMと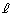 との交点をLとすると、
との交点をLとすると、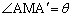 です。
です。
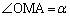 とすると、三角形OBCと平面Pの間の角は
とすると、三角形OBCと平面Pの間の角は となりますが、直線OHが三角形ABCの周上または内部を通過しない、ということは、
となりますが、直線OHが三角形ABCの周上または内部を通過しない、ということは、 ということです。三角形OBCと平面のなす角は、鋭角側をとるのであれば、
ということです。三角形OBCと平面のなす角は、鋭角側をとるのであれば、 ということになります。OからAMに垂線OGを下ろすと、Gは三角形ABCの重心で、AG:GM=2:1より、
ということになります。OからAMに垂線OGを下ろすと、Gは三角形ABCの重心で、AG:GM=2:1より、 正射影 ,つまり、四角形
,つまり、四角形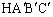 の面積は、
の面積は、 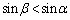 より
より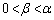 なので、
なので、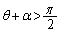 であれば、
であれば、 となり得ます。よって、
となり得ます。よって、 の最大値は
の最大値は です。Hが、三角形
です。Hが、三角形 と辺
と辺 を介して隣接している領域、辺
を介して隣接している領域、辺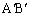 を介して隣接している領域にある場合も同様です。
を介して隣接している領域にある場合も同様です。以上より、 の形状は三角形または四角形で、その最大値は
の形状は三角形または四角形で、その最大値は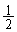 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。