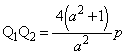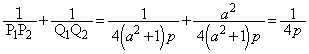���嗝�H���w'13�N[1]
������C�F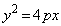 (
(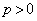 )�̏œ_F
)�̏œ_F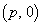 ��ʂ�2����
��ʂ�2����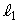 �C
�C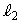 �݂͌��ɒ������AC��
�݂͌��ɒ������AC��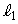 ��2�_
��2�_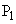 �C
�C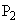 �ŁAC��
�ŁAC��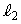 ��2�_
��2�_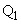 �C
�C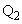 �Ō����Ƃ���B���̖₢�ɓ�����B
�Ō����Ƃ���B���̖₢�ɓ�����B
(1) 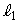 �̕�������
�̕�������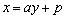 �ƒu���A
�ƒu���A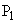 �C
�C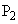 �̍��W�����ꂼ��
�̍��W�����ꂼ��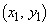 �C
�C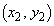 �Ƃ���B
�Ƃ���B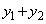 �C
�C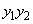 ��a��p�ŕ\���B
��a��p�ŕ\���B (2) 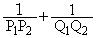 ��
��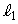 �C
�C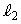 �̂Ƃ���ɂ�炸���ł��邱�Ƃ������B
�̂Ƃ���ɂ�炸���ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�܂��͌y�������炵�A�Ƃ����������̖��ł��B
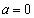 �̂Ƃ��A
�̂Ƃ��A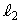 ��x��(
��x��(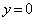 )�ƂȂ�A������C��2��_�������Ȃ��Ȃ�̂ŁA��ӂ��
)�ƂȂ�A������C��2��_�������Ȃ��Ȃ�̂ŁA��ӂ��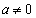 �ł��B
�ł��B
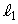 �̌X����
�̌X����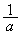 �C����Ɛ����Ȓ���
�C����Ɛ����Ȓ���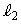 �̌X����
�̌X����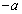 (2�����̕��s�Ɛ������Q��)�C
(2�����̕��s�Ɛ������Q��)�C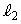 ��F
��F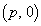 ��ʂ邩��A
��ʂ邩��A
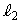 �F
�F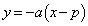 �@����B
�@����B
(1) �@�C�A��A������ƁA
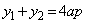 �C
�C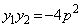 ......[��]�@����C
......[��]�@����C�܂��A�A���A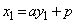 �C
�C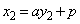 �@����D
�@����D
(2) 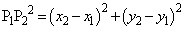
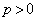 ���A
���A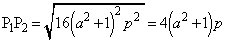 �@����E
�@����E
�@�C�B��A������ƁA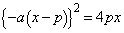
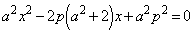 �@����F
�@����F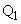 �C
�C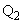 �̍��W��
�̍��W��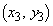 �C
�C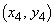 �Ƃ��āA�F��2����
�Ƃ��āA�F��2����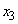 �C
�C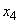 ������A���ƌW���̊W���A
������A���ƌW���̊W���A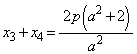 �C
�C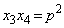 �@����G
�@����G�B���A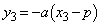 �C
�C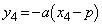 �@����H
�@����H ����ƇE���A
a�Ɉˑ����Ȃ��̂ŁA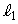 �C
�C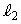 �̂Ƃ���ɂ�炸���ɂȂ�܂��B
�̂Ƃ���ɂ�炸���ɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 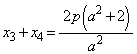 �C
�C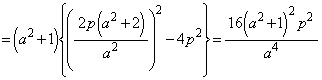 �@(�� �G)
�@(�� �G)