���嗝�H���w'22�N[2]
p�Cq�𑊈قȂ�f���Ƃ���B����3�������݂���x��2����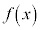 ���l����B
���l����B ���W���͂��ׂĐ�����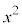 �̌W����1�ł���B
�̌W����1�ł���B
��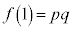 �ł���B
�ł���B
��������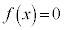 �͐����������B
�͐����������B �ȉ��̖�ɓ�����B
(1) 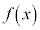 �����ׂċ��߂�B
�����ׂċ��߂�B (2) (1)�ŋ��߂����̂�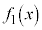 �C
�C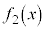 �C����C
�C����C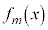 �Ƃ���B
�Ƃ���B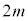 ��������
��������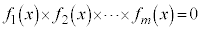 �̑��قȂ���̑��a��p�Cq�ɂ��Ȃ����Ƃ������B
�̑��قȂ���̑��a��p�Cq�ɂ��Ȃ����Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��₩�Ǝv���ƈӊO�Ƃ����ł��Ȃ��A�Ƃ������ł��B�������Œ��߂���������ƁA�ƂɋA���Ă��������邱�ƂɂȂ�܂�
(1) p�Cq�͑��قȂ�̂ŁA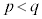 �Ƃ��čl���܂��B2���������F
�Ƃ��čl���܂��B2���������F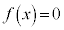 �̐�������a�C�����̉���b�Ƃ���ƁA
�̐�������a�C�����̉���b�Ƃ���ƁA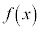 ��
��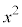 �̌W����1�Ȃ̂ŁA
�̌W����1�Ȃ̂ŁA 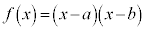 �@����@
�@����@�Ƃ����܂��B��ӂ��A
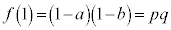 �@����A
�@����A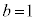 �Ƃ���ƁAp�Cq�̂����ꂩ��0�ŕs�K�ł��B
�Ƃ���ƁAp�Cq�̂����ꂩ��0�ŕs�K�ł��B
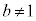 �̂Ƃ��A
�̂Ƃ��A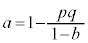 �������Ȃ̂ŁA
�������Ȃ̂ŁA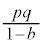 �������ł��Bp�Cq�͑��قȂ�f���Ȃ̂ŁA
�������ł��Bp�Cq�͑��قȂ�f���Ȃ̂ŁA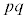 �̖́A1�Cp�Cq�C
�̖́A1�Cp�Cq�C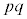 ��4�݂̂ŁA
��4�݂̂ŁA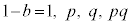 �Ɍ����܂��B�܂�Ab�������ł��B������A�A���݂������ׂĂ�
�Ɍ����܂��B�܂�Ab�������ł��B������A�A���݂������ׂĂ�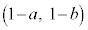 �̑g�ݍ��킹�́Aa�Cb�Ƃ��ɐ����Ȃ̂ŁA
�̑g�ݍ��킹�́Aa�Cb�Ƃ��ɐ����Ȃ̂ŁA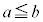 �Ƃ��āA
�Ƃ��āA����āA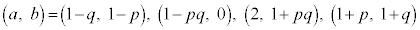 �@����B
�@����B
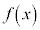 �̑S�ẮA�@���A
�̑S�ẮA�@���A
(2) (1)���A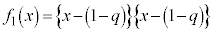 �C
�C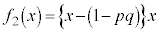 �C
�C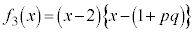 �C
�C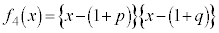 �C
�C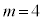 �Ȃ̂ŁA
�Ȃ̂ŁA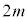 ����������8���������F
����������8���������F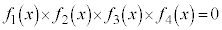 �ł��B
�ł��B ���̉��́A�B���A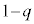 �C
�C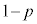 �C
�C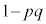 �C0�C2�C
�C0�C2�C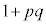 �C
�C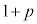 �C
�C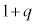 �@����C
�@����C
�����ŁA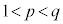 �C
�C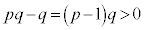 ���A
���A  �C
�C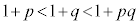 �C
�C�܂��A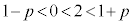 ���A
���A �ƂȂ�A�C�̉��͂��ׂđ��قȂ�܂��B����āA���̑��a�́A
����āA���̑��a��p�Cq�͂�炸�A��ӂ͎�����܂����B
���D��ӂ́Ap�Cq���f���łȂ��Ă��������܂��B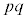 �̖̂�������������
�̖̂�������������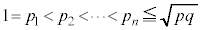 �Ƃ��āA
�Ƃ��āA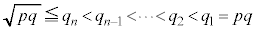 �C�܂��A
�C�܂��A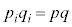 (
(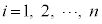 )�ƂȂ�悤��
)�ƂȂ�悤��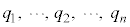 �����߂�ƁA
�����߂�ƁA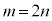 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A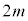 ���������́A
���������́A �ƂȂ�A(2)�̉��̑��a�́A
�ƂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B