早稲田大学基幹・創造・先進理工学部2022年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 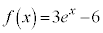 ,
,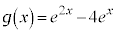 とおく。xy平面上の曲線
とおく。xy平面上の曲線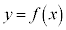 をC,曲線
をC,曲線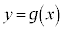 をDとする。以下の問に答えよ。
をDとする。以下の問に答えよ。
(1) CとDの概形を一つのxy平面上に描け。
(2) CとDによって囲まれた部分の面積Sを求めよ。
(3) CとDによって囲まれた部分を、x軸の周りに1回転させてできる立体の体積Vを求めよ。
[解答へ]
[2] p,qを相異なる整数とする。次の3条件をみたすxの2次式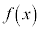 を考える。
を考える。 ●係数はすべて整数で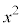 の係数は1である。
の係数は1である。
●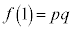 である。
である。
●方程式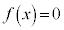 は整数解をもつ。
は整数解をもつ。 以下の問に答えよ。
(1) 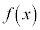 をすべて求めよ。
をすべて求めよ。 (2) (1)で求めたものを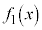 ,
,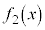 ,・・・,
,・・・,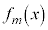 とする。
とする。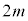 次方程式
次方程式 の相異なる解の総和はp,qによらないことを示せ。
の相異なる解の総和はp,qによらないことを示せ。 [解答へ]
[3] rを実数とする。次の条件によって定められる数列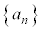 ,
,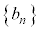 ,
,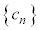 を考える。
を考える。
ただし、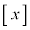 はxを超えない最大の整数とする。以下の問に答えよ。
はxを超えない最大の整数とする。以下の問に答えよ。
(1) 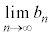 と
と を求めよ。
を求めよ。 (2)  (
(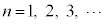 )を示せ。
)を示せ。 (3) 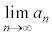 を求めよ。
を求めよ。 [解答へ]
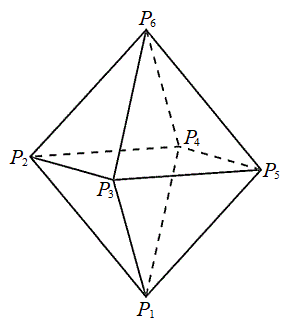 [4] 一辺の長さが
[4] 一辺の長さが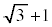 である正八面体の頂点を右図のように
である正八面体の頂点を右図のように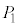 ,
,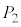 ,
,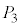 ,
,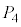 ,
,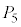 ,
, とする。各
とする。各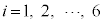 に対して、
に対して、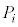 以外の5点を頂点とする四角錐(すい)のすべての面に内接する球(内部を含む)を
以外の5点を頂点とする四角錐(すい)のすべての面に内接する球(内部を含む)を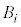 とする。
とする。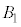 の体積をXとし、
の体積をXとし、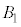 と
と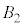 の共通部分の体積をYとし、
の共通部分の体積をYとし、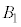 ,
,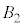 ,
,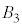 の共通部分の体積をZとする。さらに、
の共通部分の体積をZとする。さらに、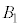 ,
,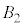 ,・・・,
,・・・,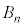 を合わせて得られる立体の体積を
を合わせて得られる立体の体積を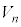 (
(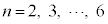 )とする。以下の問に答えよ。ただし、(1)は答のみを解答用紙の該当欄に書け。
)とする。以下の問に答えよ。ただし、(1)は答のみを解答用紙の該当欄に書け。
(1) 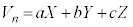 となる整数a,b,cを
となる整数a,b,cを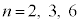 の場合について求めよ。
の場合について求めよ。 (2) Xの値を求めよ。
(3) 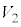 の値を求めよ。
の値を求めよ。 [解答へ]
[5] 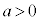 を定数とし、
を定数とし、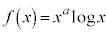 とする。以下の問に答えよ。
とする。以下の問に答えよ。
(1) 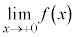 を求めよ。必要ならば
を求めよ。必要ならば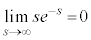 が成り立つことは証明なしに用いてよい。
が成り立つことは証明なしに用いてよい。 (2) 曲線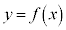 の変曲点がx軸上に存在するときのaの値を求めよ。さらにそのとき
の変曲点がx軸上に存在するときのaの値を求めよ。さらにそのとき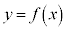 のグラフの概形を描け。
のグラフの概形を描け。 (3) 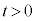 に対して、曲線
に対して、曲線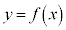 上の点
上の点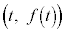 における接線を
における接線を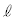 とする。
とする。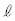 がy軸の負の部分と交わるための
がy軸の負の部分と交わるための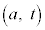 の条件を求め、その条件の表す領域をat平面上に図示せよ。
の条件を求め、その条件の表す領域をat平面上に図示せよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。