���嗝�H���w'22�N[5]
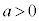 ��萔�Ƃ��A
��萔�Ƃ��A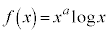 �Ƃ���B�ȉ��̖�ɓ�����B
�Ƃ���B�ȉ��̖�ɓ�����B
(1) 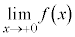 �����߂�B�K�v�Ȃ��
�����߂�B�K�v�Ȃ��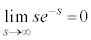 �����藧���Ƃ͏ؖ��Ȃ��ɗp���Ă悢�B
�����藧���Ƃ͏ؖ��Ȃ��ɗp���Ă悢�B (2) �Ȑ�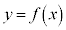 �̕ϋȓ_��x����ɑ��݂���Ƃ���a�̒l�����߂�B����ɂ��̂Ƃ�
�̕ϋȓ_��x����ɑ��݂���Ƃ���a�̒l�����߂�B����ɂ��̂Ƃ�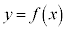 �̃O���t�̊T�`��`���B
�̃O���t�̊T�`��`���B (3) 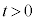 �ɑ��āA�Ȑ�
�ɑ��āA�Ȑ�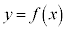 ��̓_
��̓_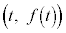 �ɂ�����ڐ���
�ɂ�����ڐ���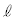 �Ƃ���B
�Ƃ���B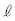 ��y���̕��̕����ƌ���邽�߂�
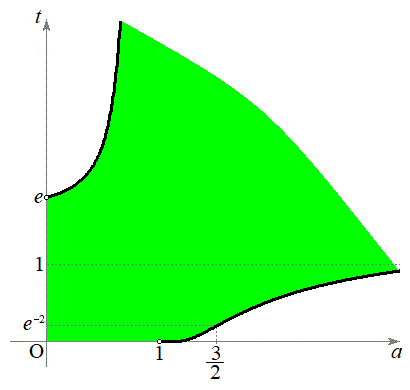
��y���̕��̕����ƌ���邽�߂�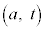 �̏��������߁A���̏����̕\���̈��at���ʏ�ɐ}������B
�̏��������߁A���̏����̕\���̈��at���ʏ�ɐ}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@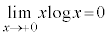 �������Ƃ��A
�������Ƃ��A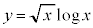 (
(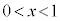 )�̍ŏ��lm (
)�̍ŏ��lm (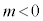 )�����߁A
)�����߁A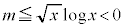 �̊e�ӂ�
�̊e�ӂ�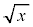 �������āA
�������āA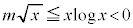 �Ƃ��A
�Ƃ��A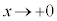 �Ƃ��Ă͂��݂����ɂ���Ƃ����̂��퓅��i�ł��B�{��ł́A
�Ƃ��Ă͂��݂����ɂ���Ƃ����̂��퓅��i�ł��B�{��ł́A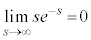 ���g���A�Ƃ����w�������Ă��܂��B
���g���A�Ƃ����w�������Ă��܂��B
(1)  �ɂ����āA
�ɂ����āA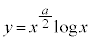 ���l���܂��B��������ƁA
���l���܂��B��������ƁA 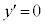 �Ƃ���ƁA
�Ƃ���ƁA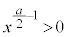 ���A
���A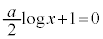 �@��
�@�� 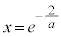 �@(�ΐ������Q��)
�@(�ΐ������Q��)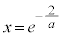 �̂Ƃ��A
�̂Ƃ��A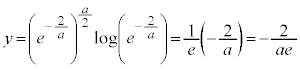 �����\�́A�ȉ��̂悤�ɂȂ�܂��B�����\���A
�����\�́A�ȉ��̂悤�ɂȂ�܂��B�����\���A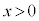 �ɂ����āA
�ɂ����āA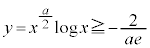 �C
�C
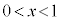 �ɂ����ẮA
�ɂ����ẮA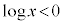 ���A
���A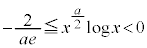
�e�ӂ�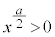 ��������ƁA
��������ƁA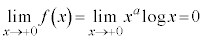 ......[��]
......[��]�ʉ��D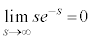 �𗘗p����A�Ƃ����q���g�����Ă���̂ŁA
�𗘗p����A�Ƃ����q���g�����Ă���̂ŁA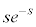 ��
��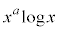 �Ƃ�����ׂāA
�Ƃ�����ׂāA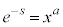 �Ƃ������ӂ̑ΐ����l���A
�Ƃ������ӂ̑ΐ����l���A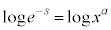 �C
�C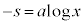
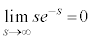 �ɂ����āA
�ɂ����āA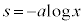 �Ƃ�����
�Ƃ�����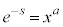 �ł����āA
�ł����āA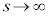 �̂Ƃ�
�̂Ƃ�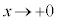 �ƂȂ�A
�ƂȂ�A 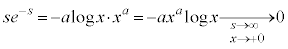 �@��
�@�� 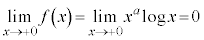
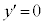 �Ƃ���ƁA
�Ƃ���ƁA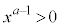 ���A
���A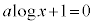 �@��
�@�� 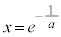
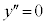 �Ƃ���ƁA
�Ƃ���ƁA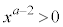 ���A
���A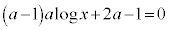 �ƂȂ�܂����A
�ƂȂ�܂����A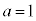 �̂Ƃ��ɂ͉����Ȃ��A
�̂Ƃ��ɂ͉����Ȃ��A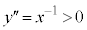 ���A�ϋȓ_�͂ł��܂���B
���A�ϋȓ_�͂ł��܂���B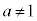 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A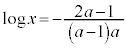 �@��
�@�� 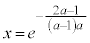
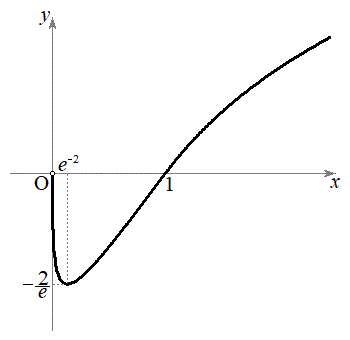 ���̂Ƃ��A
���̂Ƃ��A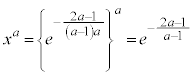 ���A�ϋȓ_��x����ɑ��݂���Ƃ��A
���A�ϋȓ_��x����ɑ��݂���Ƃ��A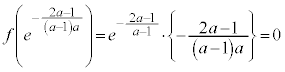 �@��
�@�� 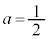 ......[��]
......[��]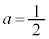 �̂Ƃ��A
�̂Ƃ��A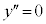 �ƂȂ�x�́A
�ƂȂ�x�́A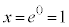 �C���̂Ƃ�
�C���̂Ƃ�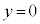
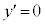 �ƂȂ�x�́A
�ƂȂ�x�́A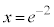 �C���̂Ƃ���y�́A
�C���̂Ƃ���y�́A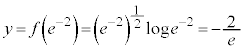 �����\�́A
�����\�́A| x | 0 | �@ | 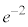 | �@ | 1 | �@ |
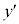 | �~ | �| | 0 | �{ | �{ | �{ |
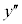 | �~ | �{ | �{ | �{ | 0 | �| |
| y | �~ |  | 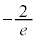 |  | 0 |  |
�����\��(1)���A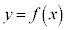 �̃O���t�͉E�}(���̂Ƃ��A�m���ɕϋȓ_��x����ɑ��݂��܂�)�B
�̃O���t�͉E�}(���̂Ƃ��A�m���ɕϋȓ_��x����ɑ��݂��܂�)�B
(3) 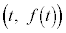 �ɂ������ڐ�
�ɂ������ڐ�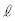 �́A
�́A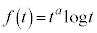 �C
�C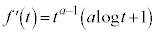 (�� �@)���A
(�� �@)���A 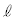 ��y���̕��̕����ƌ���邽�߂ɁA
��y���̕��̕����ƌ���邽�߂ɁA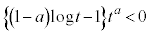 �@����A
�@����A
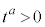 ���A
���A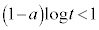
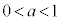 �̂Ƃ��A
�̂Ƃ��A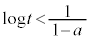 �C
�C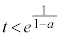 �@����B
�@����B
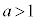 �̂Ƃ��A
�̂Ƃ��A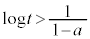 �C
�C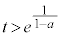 �@����C
�@����C
 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A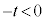 �܂�
�܂�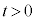 �@����D
�@����D
�����ŁA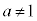 �Ƃ��āA��
�Ƃ��āA��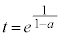 (
(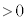 )���l���܂��B
)���l���܂��B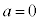 �̂Ƃ�
�̂Ƃ�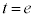
| a | 0 | �@ | 1 | �@ | 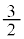 | �@ |
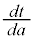 | �{ | �{ | �~ | �{ | �{ | �{ |
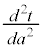 | �{ | �{ | �~ | �{ | 0 | �| |
| t | e |  | �~ |  | 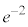 |  |
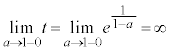 �C
�C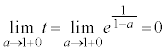 �C
�C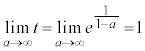
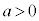 �C�B�C�C�C�D���A���߂��̈���}������ƁA�E�}���ΐF���F��(���E���������)�B
�C�B�C�C�C�D���A���߂��̈���}������ƁA�E�}���ΐF���F��(���E���������)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 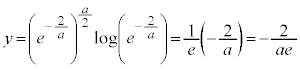
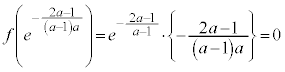 �@��
�@�� 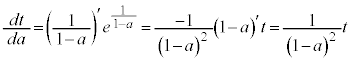 (
(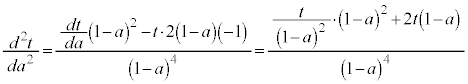

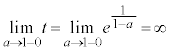 �C
�C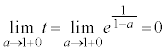 �C
�C