���嗝�H���w'22�N[1]
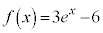 �C
�C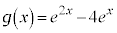 �Ƃ����Bxy���ʏ�̋Ȑ�
�Ƃ����Bxy���ʏ�̋Ȑ�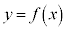 ��C�C�Ȑ�
��C�C�Ȑ�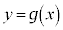 ��D�Ƃ���B�ȉ��̖�ɓ�����B
��D�Ƃ���B�ȉ��̖�ɓ�����B
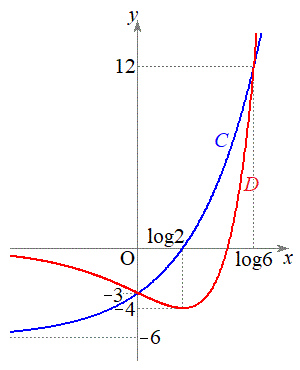
(1) C��D�̊T�`�����xy���ʏ�ɕ`���B
(2) C��D�ɂ���Ĉ͂܂ꂽ�����̖ʐ�S�����߂�B
(3) C��D�ɂ���Ĉ͂܂ꂽ�������Ax���̎����1��]�����Ăł��闧�̂̑̐�V�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(3)�̐ϕ��́A����͂���܂��A����킵�����ɖʓ|�ŁA�������ł͌�ɂ���̂������ł��B
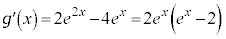 �C
�C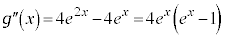 �@(�������̔����@���Q��)
�@(�������̔����@���Q��)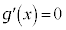 �Ƃ���ƁA
�Ƃ���ƁA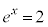 �C
�C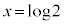 �@(�ΐ������Q�ƁB�ȉ��ɂ����āA
�@(�ΐ������Q�ƁB�ȉ��ɂ����āA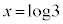 �̂Ƃ�
�̂Ƃ�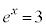 �C
�C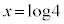 �̂Ƃ�
�̂Ƃ�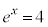 �C
�C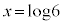 �̂Ƃ�
�̂Ƃ�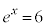 �ƂȂ�܂�)
�ƂȂ�܂�)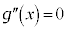 �Ƃ���ƁA
�Ƃ���ƁA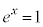 �C
�C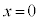
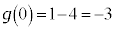 �C
�C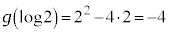 �C�ȏ���A
�C�ȏ���A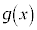 �̑����\�͈ȉ��̂悤�ɂȂ�܂��B
�̑����\�͈ȉ��̂悤�ɂȂ�܂��B| x | �@ | 0 | �@ | 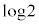 | �@ |
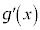 | �| | �| | �| | 0 | �{ |
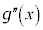 | �| | 0 | �{ | �{ | �{ |
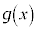 |  | 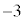 |  | 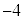 |  |
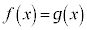 �Ƃ���ƁA
�Ƃ���ƁA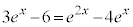
C�CD�́A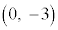 �C
�C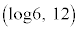 �ɂ����Č����܂��B
�ɂ����Č����܂��B
�܂��A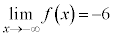 �C
�C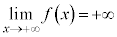 �C
�C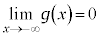 �C
�C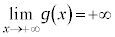
�ȏ���AC��D�̊T�`�́A�E�}�̂悤�ɂȂ�܂��B
(2) 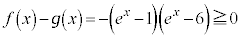 �Ƃ���ƁA
�Ƃ���ƁA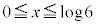
C��D�ɂ���Ĉ͂܂ꂽ�����́A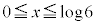 �͈̔͂ɂ���܂��B����āA�����ʐ�S�́A
�͈̔͂ɂ���܂��B����āA�����ʐ�S�́A 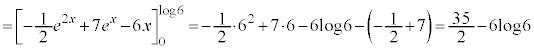 ......[��]
......[��]
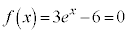 �Ƃ���ƁA
�Ƃ���ƁA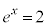 �@��
�@�� 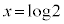
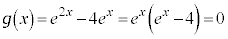 �Ƃ���ƁA
�Ƃ���ƁA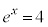 �@��
�@�� 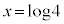
(1)�̉̃O���t��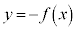 �C
�C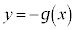 �̃O���t���d�˂ĕ`���ƉE�}�̂悤�ɂȂ�܂��B�O���t���AC��D�ɂ���Ĉ͂܂ꂽ����(���F���F��)���Ax���̎����1��]������ƁA�O���ɗ���̂́A
�̃O���t���d�˂ĕ`���ƉE�}�̂悤�ɂȂ�܂��B�O���t���AC��D�ɂ���Ĉ͂܂ꂽ����(���F���F��)���Ax���̎����1��]������ƁA�O���ɗ���̂́A
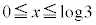 �ɂ����Ă�D�F
�ɂ����Ă�D�F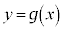 �C
�C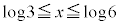 �ɂ����Ă�C�F
�ɂ����Ă�C�F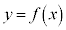 �ł��B
�ł��B
��]�̂̓����ł��蔲���镔���̋��E�ɗ���̂́A
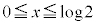 �ɂ����Ă�C�F
�ɂ����Ă�C�F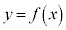 �C
�C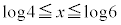 �ɂ����Ă�D�F
�ɂ����Ă�D�F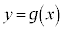 �ł��B
�ł��B
������A���߂����̂̑̐�V�́A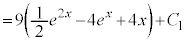 �@(
�@(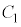 �F�ϕ��萔)
�F�ϕ��萔)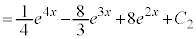 �@(
�@(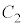 �F�ϕ��萔)
�F�ϕ��萔)�Ƃ��āA�ȉ��A�ϕ��萔���ȗ�����ƁA
�������@�ɑ�����āA
�� 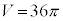 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B