���嗝�H���w'22�N[4]
 ��ӂ̒�����
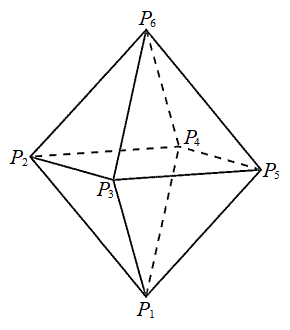
��ӂ̒�����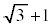 �ł��鐳���ʑ̂̒��_���E�}�̂悤��
�ł��鐳���ʑ̂̒��_���E�}�̂悤��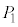 �C
�C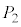 �C
�C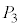 �C
�C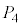 �C
�C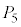 �C
�C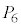 �Ƃ���B�e
�Ƃ���B�e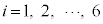 �ɑ��āA
�ɑ��āA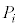 �ȊO��5�_�_�Ƃ���l�p��(����)�̂��ׂĂ̖ʂɓ��ڂ��鋅(�������܂�)��
�ȊO��5�_�_�Ƃ���l�p��(����)�̂��ׂĂ̖ʂɓ��ڂ��鋅(�������܂�)��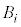 �Ƃ���B
�Ƃ���B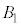 �̑̐ς�X�Ƃ��A
�̑̐ς�X�Ƃ��A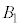 ��
��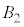 �̋��ʕ����̑̐ς�Y�Ƃ��A
�̋��ʕ����̑̐ς�Y�Ƃ��A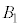 �C
�C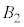 �C
�C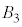 �̋��ʕ����̑̐ς�Z�Ƃ���B����ɁA
�̋��ʕ����̑̐ς�Z�Ƃ���B����ɁA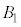 �C
�C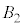 �C����C
�C����C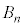 �����킹�ē����闧�̂̑̐ς�
�����킹�ē����闧�̂̑̐ς�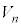 (
(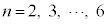 )�Ƃ���B�ȉ��̖�ɓ�����B�������A(1)�͓��݂̂��p���̊Y�����ɏ����B
)�Ƃ���B�ȉ��̖�ɓ�����B�������A(1)�͓��݂̂��p���̊Y�����ɏ����B
(1) 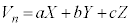 �ƂȂ鐮��a�Cb�Cc��
�ƂȂ鐮��a�Cb�Cc��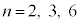 �̏ꍇ�ɂ��ċ��߂�B
�̏ꍇ�ɂ��ċ��߂�B (2) X�̒l�����߂�B
(3) 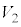 �̒l�����߂�B
�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@����c�炵���I���W�i���e�B�[������ŁA��Ԋ��o���K�v�ł��B
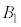 �͐��l�p��
�͐��l�p��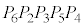 �ɓ��ڂ��鋅�A
�ɓ��ڂ��鋅�A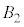 �͐��l�p��
�͐��l�p��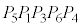 �ɓ��ڂ��鋅�A
�ɓ��ڂ��鋅�A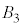 �͐��l�p��
�͐��l�p��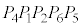 �ɓ��ڂ��鋅�ł��B
�ɓ��ڂ��鋅�ł��B
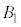 ��
��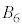 �͐����`
�͐����`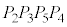 �Ŋu�Ă��Ă���̂ŁA
�Ŋu�Ă��Ă���̂ŁA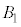 ��
��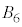 �ɂ͋��ʕ����͂���܂���B
�ɂ͋��ʕ����͂���܂���B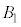 ��
��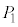 �ȊO��5�_�A
�ȊO��5�_�A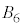 ��
��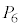 �ȊO��5�_���A���ꂼ��5���_�Ƃ���l�p���ɓ��ڂ��鋅�ł����āA
�ȊO��5�_���A���ꂼ��5���_�Ƃ���l�p���ɓ��ڂ��鋅�ł����āA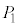 ��
��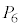 �͐����ʑ̂̑Ό����钸�_�ł��B���l��
�͐����ʑ̂̑Ό����钸�_�ł��B���l��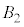 ��
��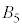 �C
�C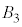 ��
��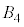 �ɂ͋��ʕ����͂���܂���B
�ɂ͋��ʕ����͂���܂���B
�����ʑ̂̑Ώ̐�����A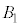 ��
��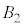 �̈ʒu�W�A
�̈ʒu�W�A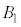 ��
��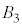 �̈ʒu�W�A
�̈ʒu�W�A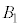 ��
��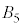 �̈ʒu�W�A
�̈ʒu�W�A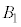 ��
��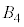 �̈ʒu�W�͓������A���̋��ʕ����̑̐ς�Y�ł��B�܂��A
�̈ʒu�W�͓������A���̋��ʕ����̑̐ς�Y�ł��B�܂��A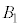 ��
��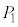 �ȊO��5�_�A
�ȊO��5�_�A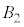 ��
��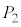 �ȊO��5�_���A���ꂼ��5���_�Ƃ���l�p���ɓ��ڂ��鋅�ł����āA
�ȊO��5�_���A���ꂼ��5���_�Ƃ���l�p���ɓ��ڂ��鋅�ł����āA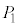 ��
��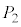 �͐����ʑ̂�1�ӂ̗��[�ƂȂ�אڒ��_�ł��B
�͐����ʑ̂�1�ӂ̗��[�ƂȂ�אڒ��_�ł��B
6�̒��_����2�̒��_��I�ԑI�ѕ��́A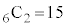 �ʂ�(�g�ݍ��킹���Q��)����܂����A���̂����Ό����钸�_�̑g���A
�ʂ�(�g�ݍ��킹���Q��)����܂����A���̂����Ό����钸�_�̑g���A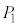 ��
��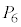 �C
�C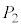 ��
��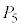 �C
�C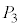 ��
��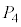 ��3�ʂ肠��A
��3�ʂ肠��A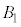 ��
��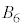 �C
�C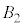 ��
��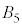 �C
�C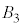 ��
��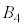 ��3�ʂ�ɂ͋��ʕ���������܂���B�אڒ��_�̑g�ݍ��킹�͎c���12�ʂ�ŁA�����̑g�ݍ��킹�ł́A���ʕ����̑̐ς�Y�ƂȂ�܂��B�@����@
��3�ʂ�ɂ͋��ʕ���������܂���B�אڒ��_�̑g�ݍ��킹�͎c���12�ʂ�ŁA�����̑g�ݍ��킹�ł́A���ʕ����̑̐ς�Y�ƂȂ�܂��B�@����@
�܂��A�����`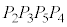 �̒��S�A�����A����
�̒��S�A�����A����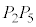 �Ɛ���
�Ɛ���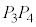 �̌�_��O�Ƃ���ƁA
�̌�_��O�Ƃ���ƁA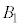 �͐����`
�͐����`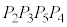 ����
����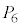 ���Ɉʒu���A
���Ɉʒu���A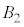 �͐����`
�͐����`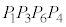 ����
����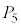 ���Ɉʒu���A
���Ɉʒu���A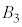 �͐����`
�͐����`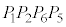 ����
����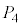 ���Ɉʒu���A�����`
���Ɉʒu���A�����`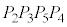 �C�����`
�C�����`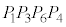 �C�����`
�C�����`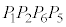 ��1�_O�����L���Ă��āA
��1�_O�����L���Ă��āA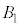 �C
�C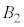 �C
�C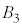 �̋��ʕ����͎O�p��
�̋��ʕ����͎O�p��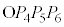 (1�_O�Ɛ����ʑ̂�1���ʂƂłł���O�p��)�̒��ɂ���A���̑̐ς�Z�ł��B
(1�_O�Ɛ����ʑ̂�1���ʂƂłł���O�p��)�̒��ɂ���A���̑̐ς�Z�ł��B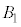 �C
�C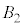 �C
�C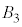 �Ɠ����ʒu�W�ɂ���̂́A�����ʑ̂�8�̑��ʂ����̂ŁA���ɁA
�Ɠ����ʒu�W�ɂ���̂́A�����ʑ̂�8�̑��ʂ����̂ŁA���ɁA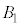 �C
�C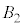 �C
�C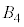 �ȂǁA8�ʂ肠��܂��B�@����A
�ȂǁA8�ʂ肠��܂��B�@����A
6�̒��_����3��I�ԑI�ѕ��́A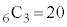 �ʂ肠��܂����A��L��8�ʂ�ȊO�A�Ⴆ��
�ʂ肠��܂����A��L��8�ʂ�ȊO�A�Ⴆ��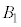 �C
�C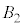 �C
�C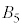 �̂悤�ɁA
�̂悤�ɁA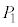 ���܂܂Ȃ����܊p���A
���܂܂Ȃ����܊p���A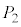 ���܂܂Ȃ����܊p���A
���܂܂Ȃ����܊p���A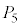 ���܂܂Ȃ����܊p���ɓ��ڂ��鋅�̑g�ݍ��킹�ł́A
���܂܂Ȃ����܊p���ɓ��ڂ��鋅�̑g�ݍ��킹�ł́A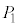 �C
�C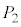 �C
�C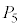 �������ʑ̂̑��ʂłȂ���
�������ʑ̂̑��ʂłȂ���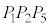 ���Ȃ��A
���Ȃ��A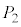 ��
��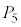 ���Ό����钸�_�Ȃ̂ŁA
���Ό����钸�_�Ȃ̂ŁA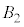 ��
��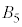 �����ʕ������������A3�̋�
�����ʕ������������A3�̋�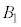 �C
�C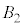 �C
�C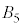 �ł����ʕ����������܂���B
�ł����ʕ����������܂���B
4�̋��A�Ⴆ��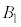 �C
�C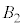 �C
�C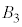 �C
�C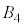 �ł́A
�ł́A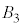 ��
��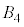 �����ʕ����������Ȃ����߁A4�̋��ŋ��ʕ����������܂���B
�����ʕ����������Ȃ����߁A4�̋��ŋ��ʕ����������܂���B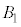 �C
�C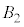 �C
�C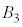 �C
�C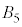 �ł�
�ł�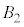 ��
��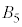 �����ʕ������������A
�����ʕ������������A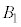 �C
�C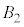 �C
�C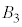 �C
�C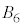 �ł�
�ł�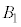 ��
��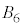 �����ʕ����������܂���B���̂悤�ɁA���ʕ����������Ȃ�2�̋��̑g���ł��Ă��܂��̂ŁA4�̋��ł́A���ʕ������ł��܂���B5�̋��A6�̋��ł����l�ɁA���ʕ����͂ł��܂���B
�����ʕ����������܂���B���̂悤�ɁA���ʕ����������Ȃ�2�̋��̑g���ł��Ă��܂��̂ŁA4�̋��ł́A���ʕ������ł��܂���B5�̋��A6�̋��ł����l�ɁA���ʕ����͂ł��܂���B
��L�̍l�@��_�q����̂�������߁A(1)�ł͉݂̂ł悢���ƂɂȂ��Ă��܂����A�_�q�s�v�ł��l�@���邱�Ƃ͕K�v�ł��B
(1) 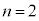 �̏ꍇ�A
�̏ꍇ�A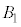 ��
��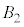 �����킹�ē����闧�̂̑̐�
�����킹�ē����闧�̂̑̐�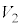 �́A
�́A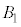 �C
�C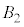 ��2�̋��̑̐ς̘a
��2�̋��̑̐ς̘a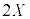 ����A���ʕ����̑̐�Y�������āA
����A���ʕ����̑̐�Y�������āA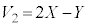 �@����B
�@����B 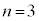 �̏ꍇ�A
�̏ꍇ�A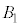 ��
��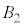 ��
��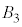 �����킹�ē����闧�̂̑̐�
�����킹�ē����闧�̂̑̐�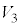 �́A
�́A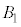 �C
�C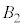 �C
�C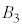 ��3�̋��̑̐ς̘a
��3�̋��̑̐ς̘a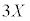 ����A
����A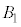 ��
��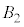 �̋��ʕ����A
�̋��ʕ����A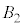 ��
��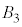 ���ʕ����A
���ʕ����A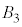 ��
��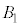 �̋��ʕ����̑̐ς̘a
�̋��ʕ����̑̐ς̘a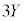 �������A����������
�������A����������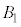 ��
��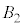 ��
��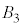 �̋��ʕ����̑̐�Z������������(���������l�����́A�W���̗v�f�̐��̍l�����Ɠ��l�ł�)�A
�̋��ʕ����̑̐�Z������������(���������l�����́A�W���̗v�f�̐��̍l�����Ɠ��l�ł�)�A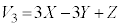 �@����C
�@����C
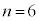 �̏ꍇ�A4�ȏ�̋��ɂ͋��ʕ������Ȃ��̂ŁA
�̏ꍇ�A4�ȏ�̋��ɂ͋��ʕ������Ȃ��̂ŁA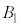 �C
�C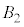 �C����C
�C����C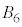 �����킹�ē����闧�̂̑̐�
�����킹�ē����闧�̂̑̐�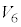 �́A6�̋��̑̐ς̘a����A�@���12�ʂ��2�̋��̋��ʕ����̐ς������A�A���8�ʂ��3�̋��̋��ʕ����̐ς����������āA
�́A6�̋��̑̐ς̘a����A�@���12�ʂ��2�̋��̋��ʕ����̐ς������A�A���8�ʂ��3�̋��̋��ʕ����̐ς����������āA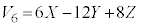 �@����D
�@����D
�B���A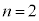 �̂Ƃ��A
�̂Ƃ��A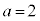 �C
�C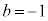 �C
�C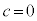 ......[��]�C���A
......[��]�C���A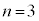 �̂Ƃ��A
�̂Ƃ��A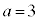 �C
�C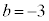 �C
�C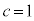 ......[��]�D���A
......[��]�D���A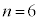 �̂Ƃ��A
�̂Ƃ��A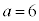 �C
�C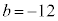 �C
�C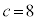 ......[��]
......[��]
�Ȍ�A�����ʑ̂�1�ӂ̒������A�O�����̒藝���g���̂ɂ��ώG�Ȃ̂ŁA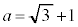 �Ƃ����܂��B
�Ƃ����܂��B
 (2) �Ⴆ��
(2) �Ⴆ��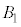 �̏ꍇ�A���̒��S��
�̏ꍇ�A���̒��S��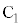 �Ƃ���ƁA
�Ƃ���ƁA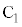 ��
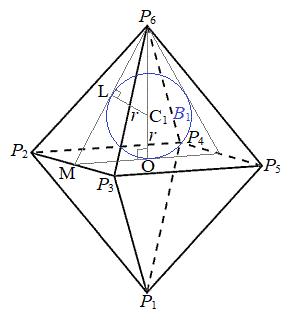
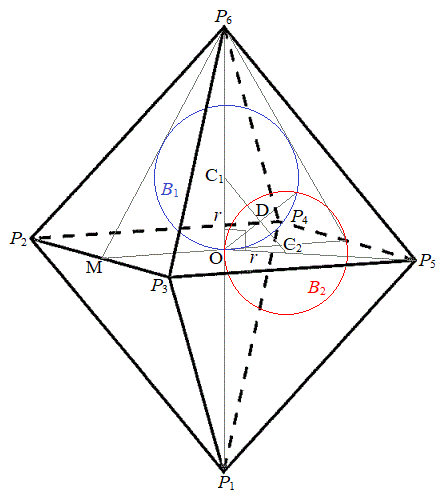
��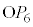 ��̓_�ŁA�E�}�̂悤�ɁA
��̓_�ŁA�E�}�̂悤�ɁA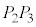 �̒��_��M�Ƃ��A
�̒��_��M�Ƃ��A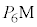 �Ƌ�
�Ƌ�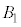 �Ƃ̐ړ_��L�Ƃ���ƁA
�Ƃ̐ړ_��L�Ƃ���ƁA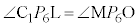 �C
�C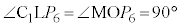 ���A��
���A��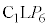 �䁢
�䁢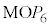 �@��
�@�� 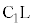 �F
�F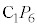 ��MO�F
��MO�F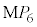 �@����E
�@����E���A��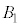 �̔��a��
�̔��a��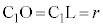 �Ƃ��āA
�Ƃ��āA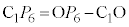 �C�E�C�F���A
�C�E�C�F���A ����āA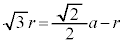 �C
�C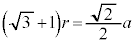
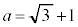 ���A
���A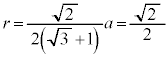 �@����G
�@����G
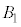 �̑̐�X�́A
�̑̐�X�́A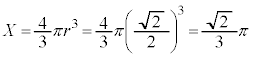 ......[��]
......[��]
 (3) ��
(3) ��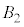 �̒��S
�̒��S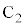 ��
��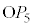 ��ɂ����āA
��ɂ����āA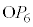 �͐����`
�͐����`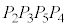 �Ɛ����Ȃ̂ŁA
�Ɛ����Ȃ̂ŁA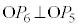 �C�܂��A
�C�܂��A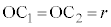 ���A��
���A��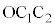 �͒��p�ӎO�p�`�ŁA�G���A
�͒��p�ӎO�p�`�ŁA�G���A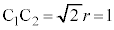 �C
�C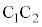 �̒��_��D�Ƃ��āA
�̒��_��D�Ƃ��āA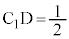 �C����āA
�C����āA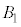 �C
�C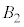 �̋��ʕ����̑̐�Y�́A
�̋��ʕ����̑̐�Y�́A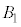 �̑̐�X�̂����A�_D��ʂ�
�̑̐�X�̂����A�_D��ʂ�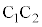 �ɐ����Ȗʂ���
�ɐ����Ȗʂ���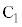 �Ƌt���̕����̑̐ς�2�{�ł��B
�Ƌt���̕����̑̐ς�2�{�ł��B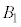 �̔��a��
�̔��a��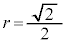 �Ȃ̂ŁA
�Ȃ̂ŁA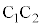 ��x���ɂƂ�A�_
��x���ɂƂ�A�_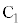 ��
��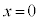 �ƂƂ���ƁA�_D��
�ƂƂ���ƁA�_D��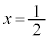 �C����
�C����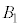 ��
��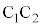 �Ƃ̌�_��
�Ƃ̌�_��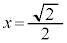 �ƂȂ�܂��B
�ƂȂ�܂��B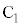 ���狗��x�̂Ƃ����
���狗��x�̂Ƃ����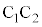 �ɐ����Ȗʂ�
�ɐ����Ȗʂ�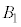 �C
�C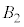 �̋��ʕ���������Ƃ��̒f�ʂɂł���~�̔��a��
�̋��ʕ���������Ƃ��̒f�ʂɂł���~�̔��a��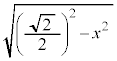 �C������A
�C������A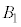 �C
�C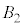 �̋��ʕ������̐�Y�́A�f�ʂ̉~�̖ʐς�x�Őϕ����邱�Ƃɂ��A
�̋��ʕ������̐�Y�́A�f�ʂ̉~�̖ʐς�x�Őϕ����邱�Ƃɂ��A�B��p���āA
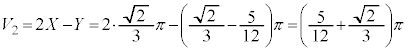 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 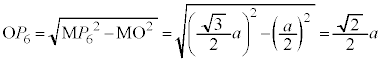 �@����F
�@����F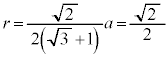 �@����G
�@����G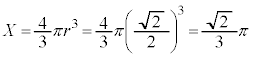 ......[��]
......[��]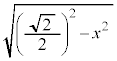 �C������A
�C������A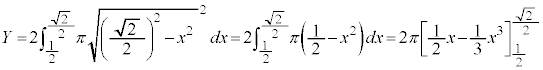
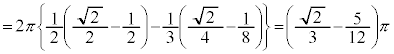
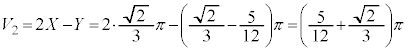 ......[��]
......[��]