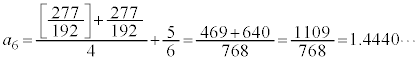���嗝�H���w'22�N[3]
r�������Ƃ���B���̏����ɂ���Ē�߂��鐔��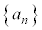 �C
�C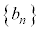 �C
�C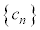 ���l����B
���l����B
�������A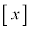 ��x���Ȃ��ő�̐����Ƃ���B�ȉ��̖�ɓ�����B
��x���Ȃ��ő�̐����Ƃ���B�ȉ��̖�ɓ�����B
(1) 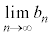 ��
��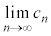 �����߂�B
�����߂�B (2) 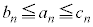 (
(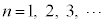 )�������B
)�������B (3) 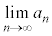 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�K�E�X�L���������Ă����ԑQ�����̖��ł��B���邱�ƂɋC�Â��Ȃ��Ɠ��ł��B�������ŐF�X�Ƃ������Ă݂邱�Ƃ��d�v�Ȗ��ł��B
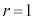 �Ƃ��āA
�Ƃ��āA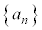 �̍ŏ��̕����v�Z���Ă݂܂��B
�̍ŏ��̕����v�Z���Ă݂܂��B
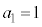 �C
�C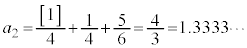 �C
�C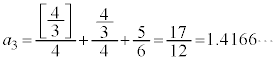 �C
�C
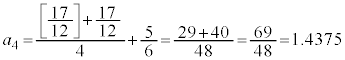 �C
�C
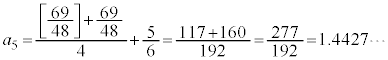 �C
�C
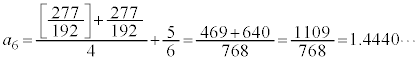
�ƂȂ�A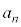 ��
��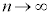 ��1��2�̊�(�����ƌ��������ς��邱�Ƃ��ł��܂���)�Ŏ������������A�Ƃ������Ƃ͂킩��܂��B
��1��2�̊�(�����ƌ��������ς��邱�Ƃ��ł��܂���)�Ŏ������������A�Ƃ������Ƃ͂킩��܂��B
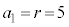 �̂Ƃ����A
�̂Ƃ����A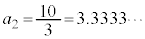 �C
�C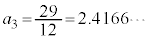 �C
�C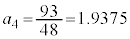 �C
�C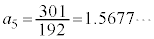 �C
�C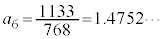
�ƂȂ�قړ��l�ł��B
���Ƃł��ꂪ�A���͂ȃq���g�ɂȂ�܂��B
(1) 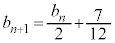 �@����@�C
�@����@�C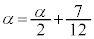 �@����A�@���
�@����A�@���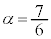
�@�|�A���A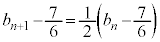
������A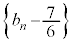 �́A����
�́A����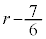 �C����
�C����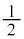 �����䐔���ŁA
�����䐔���ŁA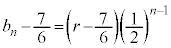
�� 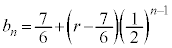
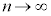 �̂Ƃ�
�̂Ƃ�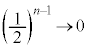 ���
��� �@��
�@�� 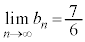 ......[��]
......[��]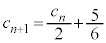 �@����B�C
�@����B�C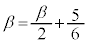 �@����C�@���
�@����C�@���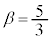
�B�|�C���A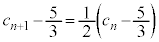
������A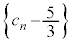 �́A����
�́A����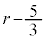 �C����
�C����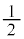 �����䐔���ŁA
�����䐔���ŁA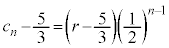
�� 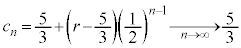 �@��
�@�� 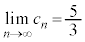 ......[��]
......[��]
(2) �K�E�X�L��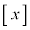 �ɂ��āA
�ɂ��āA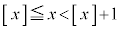 �Ƃ�������������܂��B����������ƁA
�Ƃ�������������܂��B����������ƁA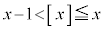 �C������A
�C������A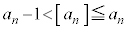 (
(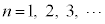 )�@����D
)�@����D ����āA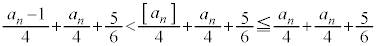
������@�C�B��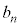 �C
�C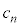 ��p���āA
��p���āA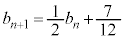 �C
�C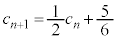 ���A
���A 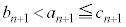 (
(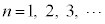 )
)
(3) (2)�̕s�������g�����͂��݂����ɂ��悤�Ƃ���ƁA(1)���A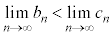 �Ȃ̂ŁA
�Ȃ̂ŁA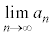 �����߂��܂���B�͂��݂����ɂ��邽�߂ɂ́A
�����߂��܂���B�͂��݂����ɂ��邽�߂ɂ́A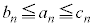 ����������������T���K�v������̂ł����A���ꂪ���s���낵�Ă��Ȃ��Ȃ�������܂���B
����������������T���K�v������̂ł����A���ꂪ���s���낵�Ă��Ȃ��Ȃ�������܂���B �����ŁA��L��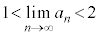 �ɂȂ肻���ȂƂ���ɖڂ�t���܂��B���ۂɂ́A(1)��(2)���A
�ɂȂ肻���ȂƂ���ɖڂ�t���܂��B���ۂɂ́A(1)��(2)���A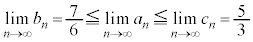 �ł��B
�ł��B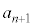 ��1�Ƃ̍��A
��1�Ƃ̍��A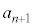 ��2�Ƃ̍��ׂĂ݂�ƁA�D���A
��2�Ƃ̍��ׂĂ݂�ƁA�D���A
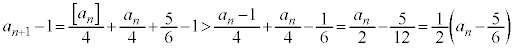 �@����E
�@����E
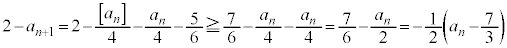 �@����F
�@����F
���鎩�R��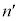 �ɑ��āA
�ɑ��āA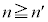 �������ׂĂ̎��R��n�ɂ��āA
�������ׂĂ̎��R��n�ɂ��āA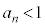 �܂���
�܂���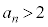 �ł���Ƃ���ƁA
�ł���Ƃ���ƁA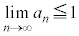 ��
��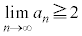 ��
��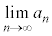 �����U���邩�ł����āA
�����U���邩�ł����āA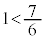 �C
�C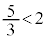 �Ȃ̂ŁA
�Ȃ̂ŁA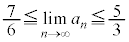 �ɂȂ蓾�܂���B
�ɂȂ蓾�܂���B
�]���āA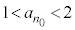 �ƂȂ鎩�R��
�ƂȂ鎩�R��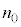 (
(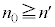 )���K�����݂��܂��B
)���K�����݂��܂��B
���鎩�R��n�ɂ��āA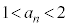 �ł���A
�ł���A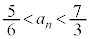 �ł���A�E�C�F���A
�ł���A�E�C�F���A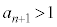 ����
����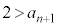 �C�܂�A
�C�܂�A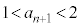 �ł��B
�ł��B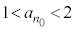 �Ȃ̂ŁA���w�I�A�[�@���A
�Ȃ̂ŁA���w�I�A�[�@���A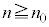 �ƂȂ邷�ׂĂ̎��R��n�ɂ��āA
�ƂȂ邷�ׂĂ̎��R��n�ɂ��āA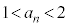 �ł��B
�ł��B
����āA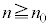 �ƂȂ邷�ׂĂ̎��R��n�ɂ��āA
�ƂȂ邷�ׂĂ̎��R��n�ɂ��āA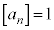 �ł��B
�ł��B
���̂Ƃ��A �@����G
�@����G
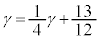 �@����H�@���A
�@����H�@���A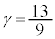
�G�|�H���A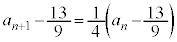
������A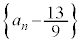 �́A����
�́A����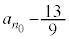 �C����
�C����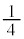 �����䐔���ŁA
�����䐔���ŁA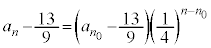
�� 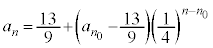 �@(
�@(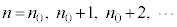 )
)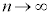 �̂Ƃ��A
�̂Ƃ��A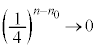 ���A
���A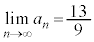 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 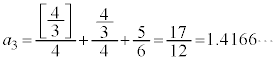 �C
�C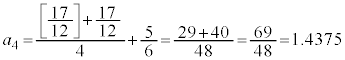 �C
�C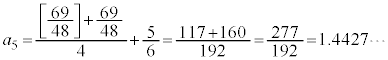 �C
�C