���嗝�H���w'23�N[2]
�ԋʂƍ��ʂ������Ă���܂̒����疳��ׂɋʂ�1���o���A���o�����ʂ�܂ɖ߂�����ŁA���o�����ʂƓ����F�̋ʂ�����1�܂ɓ���鑀����J��Ԃ��B�ȉ��̖�ɓ�����B
(1) ���߂ɑ܂̒��ɐԋʂ�1�A���ʂ�1�����Ă���Ƃ���Bn��̑�����s�����Ƃ��A�ԋʂ����傤��k����o���m����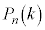 (
(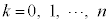 )�Ƃ���B
)�Ƃ���B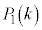 ��
��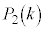 �����߁A�����
�����߁A�����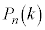 �����߂�B
�����߂�B (2) ���߂ɑ܂̒��ɐԋʂ�r�A���ʂ�b��(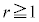 �C
�C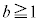 )�����Ă���Ƃ���Bn��̑�����s�����Ƃ��Ak��ڂɐԋʂ��A����ȊO�ł͂��ׂč��ʂ����o�����m����
)�����Ă���Ƃ���Bn��̑�����s�����Ƃ��Ak��ڂɐԋʂ��A����ȊO�ł͂��ׂč��ʂ����o�����m����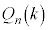 (
(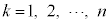 )�Ƃ���B
)�Ƃ���B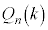 ��k�ɂ��Ȃ����Ƃ������B
��k�ɂ��Ȃ����Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���Rn�͎��R���ł��B���ł͂Ȃ��̂ŁAn�Ck�Cr�Cb�Ȃǂɋ�̓I���l�����ď�c�����A�m���ɓ��_���܂��傤�B(2)�́A�uk�ɂ��Ȃ����Ƃ������v�Ȃ̂ŁA��̓I�Ɋm�������߂Ȃ��Ă��ł���Ǝv���܂����A�ȉ��ł͊m�������߂Ă��܂��B
(1) 1���(����)�̏�ԂŁA�ԋʂ����o���m�������ʂ����o���m����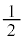 �ł��B1��ڂɐԋʂ����o��(�ԋʂ�1����o��)�ƁA�ԋʂ�2�A���ʂ�1�ɂȂ�܂��B1��ڂɍ��ʂ����o��(�ԋʂ�0����o��)�ƁA�ԋʂ�1�A���ʂ�2�ɂȂ�܂��B�ԋ�2�ɂȂ�m���A�ԋ�1�ɂȂ�m���A�Ƃ���
�ł��B1��ڂɐԋʂ����o��(�ԋʂ�1����o��)�ƁA�ԋʂ�2�A���ʂ�1�ɂȂ�܂��B1��ڂɍ��ʂ����o��(�ԋʂ�0����o��)�ƁA�ԋʂ�1�A���ʂ�2�ɂȂ�܂��B�ԋ�2�ɂȂ�m���A�ԋ�1�ɂȂ�m���A�Ƃ���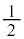 �ł��B����āA�ԋʂ�1����o���m��
�ł��B����āA�ԋʂ�1����o���m��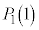 �A0����o���m��
�A0����o���m��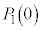 �́A
�́A 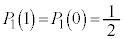 ......[��]�@����@
......[��]�@����@�ԋ�2�A����1��(������)�̏�ԂŁA�ԋʂ����o��(3�̂���2�̂ǂꂩ�����̂Ŋm��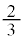 �B���ǁA�ԋʂ�2����o�����ƂɂȂ�܂�)�ƁA�ԋ�3�A����1�ɂȂ�܂����A�����m����
�B���ǁA�ԋʂ�2����o�����ƂɂȂ�܂�)�ƁA�ԋ�3�A����1�ɂȂ�܂����A�����m����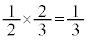 �ł��B
�ł��B
�ԋ�1�A����2��(������)�̏�ԂŁA���ʂ����o��(�m��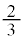 �C�ԋʂ����o����0)�ƁA�ԋ�1�A����3�ɂȂ�܂����A���̊m����
�C�ԋʂ����o����0)�ƁA�ԋ�1�A����3�ɂȂ�܂����A���̊m����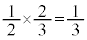 �ł��B
�ł��B
�ԋ�2�A����1��(������)�̏�Ԃō��ʂ����(�m��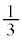 )���A�ԋ�1�A����2��(������)�̏�ԂŐԋʂ����(�m��
)���A�ԋ�1�A����2��(������)�̏�ԂŐԋʂ����(�m��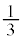 )�����ƁA�ԋʂ����o����1��ŁA�ԋ�2�A����2�ɂȂ�܂����A���̊m����
)�����ƁA�ԋʂ����o����1��ŁA�ԋ�2�A����2�ɂȂ�܂����A���̊m����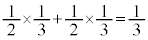 �ł��B
�ł��B
����āA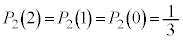 ......[��]����ŁAn���A�ԋʂ̌����A1�A2�A����An�� (�ԋʂ����o���́A���ꂼ��A0��A1��A����A
......[��]����ŁAn���A�ԋʂ̌����A1�A2�A����An�� (�ԋʂ����o���́A���ꂼ��A0��A1��A����A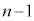 ��)�ɂȂ�m���͓�����
��)�ɂȂ�m���͓�����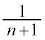 �ɂȂ�̂ł͂Ȃ����A�Ɨ\���ł��܂��B
�ɂȂ�̂ł͂Ȃ����A�Ɨ\���ł��܂��B
���߂ɑ܂̒��ɐԋʂ�1�����Ă����̂ŁA�ԋʂ�k����ƁA1���邲�Ƃɐԋʂ�1������̂ŁAn���̐ԋʂ̌��́An�쒆�ɐԋʂ����o������k��1������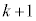 �ł��B
�ł��B
�����ŁA
����Fn��̑�����s�����Ƃ��A�ԋʂ����傤��k����o���m���A�܂�An���ɐԋʂ�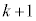 �ɂȂ��Ă���m����
�ɂȂ��Ă���m����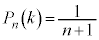 (
(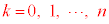 )�ł���B
)�ł���B
(�T) 1���ɐԋʂ�2�ɂȂ��Ă���m���A1�ɂȂ��Ă���m���A�܂�A1��̑���ŁA�ԋʂ�1����o���m���A0����o���m���́A�@���A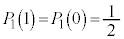 �ł��B����͐������܂��B
�ł��B����͐������܂��B (�U) m���ɐԋʂ�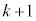 ��(
��(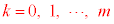 )�ɂȂ��Ă���m���A�܂�An��̑�����s�����Ƃ��A�ԋʂ�k����o���m����
)�ɂȂ��Ă���m���A�܂�An��̑�����s�����Ƃ��A�ԋʂ�k����o���m����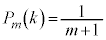 �ł���Ɖ��肵�܂��B
�ł���Ɖ��肵�܂��B m���ɁA�ԋʂƍ��ʂ����킹�āA�ŏ���2����m������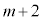 �ɂȂ�܂��B�ԋʂ�k����o���Ɛԋʂ�k������
�ɂȂ�܂��B�ԋʂ�k����o���Ɛԋʂ�k������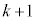 �ɂȂ�܂��B���ʂ�
�ɂȂ�܂��B���ʂ�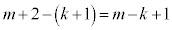 ����܂��B
����܂��B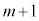 ��ڂɐԋʂ����o���m����
��ڂɐԋʂ����o���m����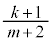 �C���ʂ����o���m����
�C���ʂ����o���m����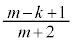 �ł��B
�ł��B
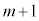 ���̐ԋʂ̌����ő�l
���̐ԋʂ̌����ő�l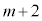 �̏ꍇ�A�ŏ��l1�̏ꍇ�A���̊Ԃ�2�`
�̏ꍇ�A�ŏ��l1�̏ꍇ�A���̊Ԃ�2�`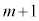 ��(�ԋʂ����o�����́A1�`m)�̏ꍇ�ɕ����Ē��ׂ܂��B
��(�ԋʂ����o�����́A1�`m)�̏ꍇ�ɕ����Ē��ׂ܂��B
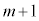 ���ɐԋʂ�
���ɐԋʂ�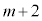 �ɂȂ�̂́Am���ɐԋʂ�
�ɂȂ�̂́Am���ɐԋʂ�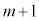 ��(m��̑��삷�ׂĂŐԋʂ����o�����̂Ŋm��
��(m��̑��삷�ׂĂŐԋʂ����o�����̂Ŋm��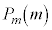 )�����Ă��āA
)�����Ă��āA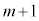 ��ڂɐԋʂ����o���ꍇ�ł��B���̂Ƃ��A
��ڂɐԋʂ����o���ꍇ�ł��B���̂Ƃ��A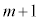 ��̑���Őԋʂ�
��̑���Őԋʂ� �����o�����ƂɂȂ�܂��B���̊m���́A
�����o�����ƂɂȂ�܂��B���̊m���́A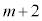 �̋ʂ���
�̋ʂ���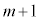 �̐ԋʂ̂ǂꂩ�����o���̂ŁA
�̐ԋʂ̂ǂꂩ�����o���̂ŁA 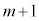 ���ɐԋʂ�1�ɂȂ�̂́Am���ɐԋʂ�1��(m��̑��삷�ׂĂō��ʂ����o�����̂Őԋʂ����o������0�C�m����
���ɐԋʂ�1�ɂȂ�̂́Am���ɐԋʂ�1��(m��̑��삷�ׂĂō��ʂ����o�����̂Őԋʂ����o������0�C�m����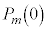 )�����Ă��āA
)�����Ă��āA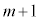 ��ڂɍ���(���ʂ̌���
��ڂɍ���(���ʂ̌���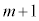 )�����o���ꍇ�ł��B���̂Ƃ��A
)�����o���ꍇ�ł��B���̂Ƃ��A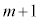 ��̑���Őԋʂ�0�����o�����ƂɂȂ�܂��B���̊m���́A
��̑���Őԋʂ�0�����o�����ƂɂȂ�܂��B���̊m���́A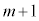 ���ɐԋʂ�
���ɐԋʂ�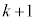 ��(
��(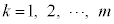 )�ɂȂ�̂́Am���ɐԋʂ�
)�ɂȂ�̂́Am���ɐԋʂ�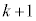 �C���ʂ�
�C���ʂ�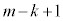 ��(�ԋʂ����o������k�C�m��
��(�ԋʂ����o������k�C�m��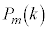 )�����Ă���Ƃ��ɍ��ʂ����o��(�m��
)�����Ă���Ƃ��ɍ��ʂ����o��(�m��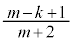 )���A�ԋʂ�k�A���ʂ�
)���A�ԋʂ�k�A���ʂ�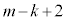 ��(�ԋʂ����o������
��(�ԋʂ����o������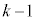 �C�m����
�C�m����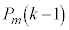 )�����Ă���Ƃ��ɐԋʂ����o��(�m��
)�����Ă���Ƃ��ɐԋʂ����o��(�m��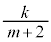 )�Ƃ��ł��B���̂Ƃ��A
)�Ƃ��ł��B���̂Ƃ��A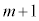 ��̑���Őԋʂ�k (
��̑���Őԋʂ�k (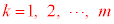 )�����o�����ƂɂȂ�܂��B�����m���́A
)�����o�����ƂɂȂ�܂��B�����m���́A�ȏ���A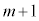 ��̑�����s�����Ƃ��A�ԋʂ�k��(
��̑�����s�����Ƃ��A�ԋʂ�k��( )���o���m����
)���o���m����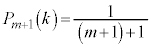 �ł���A
�ł���A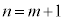 �̂Ƃ�������͐������܂��B
�̂Ƃ�������͐������܂��B (�T)�C(�U)�C���w�I�A�[�@���A���肪�������܂��B����āA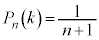 (
(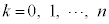 ) ......[��]
) ......[��]
(2) �Ⴆ�A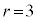 �C
�C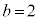 �C
�C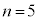 ���炢�ōl���Ă݂܂��B1��ڂɐԋʂ����o���A2��ځ`5��ڂɍ��ʂ����o���Ƃ��A
���炢�ōl���Ă݂܂��B1��ڂɐԋʂ����o���A2��ځ`5��ڂɍ��ʂ����o���Ƃ��A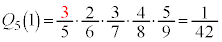 �ł��B2��ڂɐԋʂ����o���A����ȊO���ʂ��Ƃ���ƁA
�ł��B2��ڂɐԋʂ����o���A����ȊO���ʂ��Ƃ���ƁA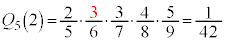 �ł��B���l�ɁA
�ł��B���l�ɁA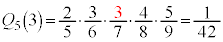 �C
�C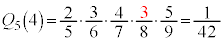 �C
�C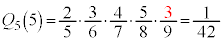 �ƂȂ�܂��B
�ƂȂ�܂��B 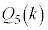 �̕���́A�e��̋ʂ̌��̐ρA�܂�A
�̕���́A�e��̋ʂ̌��̐ρA�܂�A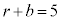 ����
����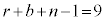 �܂ł̐ςɂȂ�܂��B���q�́Ak���(
�܂ł̐ςɂȂ�܂��B���q�́Ak���(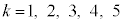 )�̂Ƃ��낾�����߂̐ԋʂ̌�
)�̂Ƃ��낾�����߂̐ԋʂ̌�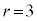 �ƂȂ�A�c��͊e��̍��ʂ̌�
�ƂȂ�A�c��͊e��̍��ʂ̌�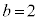 �C
�C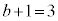 �C����C
�C����C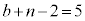 �����сA
�����сA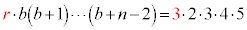 �ƂȂ��Ă��܂��B
�ƂȂ��Ă��܂��B
���߂�m���Ak���(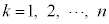 )�ɐԋʂ����o������ȊO��j���(
)�ɐԋʂ����o������ȊO��j���(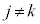 �C
�C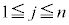 )�ɂ͍��ʂ����o���m�����l���܂��B
)�ɂ͍��ʂ����o���m�����l���܂��B
���傤��k��ڂɐԋʂ����o���m��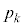 �́A�ԍ����킹���ʂ̌���
�́A�ԍ����킹���ʂ̌���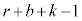 ��(�ŏ�
��(�ŏ�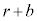 �ŁA
�ŁA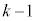 ������Ă���)�C�ԋʂ̌���r�Ȃ̂ŁA
������Ă���)�C�ԋʂ̌���r�Ȃ̂ŁA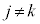 �C
�C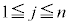 �ƂȂ鎩�R��j�ɂ���j��ڂɁA�ԍ����킹���ʂ̌���
�ƂȂ鎩�R��j�ɂ���j��ڂɁA�ԍ����킹���ʂ̌���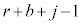 ����A�܂��A���ʂ̌���
����A�܂��A���ʂ̌���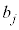 �Ƃ��āA���ʂ����o���m��
�Ƃ��āA���ʂ����o���m��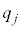 �́A
�́A���ʂ̌�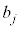 �́A�ŏ�b�ŁA
�́A�ŏ�b�ŁA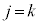 (�ԋʂ����o��)�̂Ƃ��������āA1���������An��ڂ̑O�܂łɁA
(�ԋʂ����o��)�̂Ƃ��������āA1���������An��ڂ̑O�܂łɁA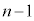 ��̂���
��̂���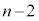 �ʂ����o��
�ʂ����o��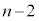 ������
������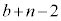 �ɂȂ�̂ŁA���ʂ̌�
�ɂȂ�̂ŁA���ʂ̌�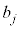 �́A
�́A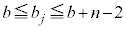 �͈̔͂̐����̒l���Ƃ�܂��B
�͈̔͂̐����̒l���Ƃ�܂��B
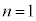 �̂Ƃ���
�̂Ƃ���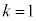 �Ɍ����܂��B
�Ɍ����܂��B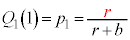 �@����A
�@����A 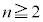 �̂Ƃ��A
�̂Ƃ��A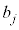 �̓����ɒ��ӂ��āA
�̓����ɒ��ӂ��āA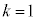 (�Ԃ�1��ڂɎ��o��)�Ȃ�A
(�Ԃ�1��ڂɎ��o��)�Ȃ�A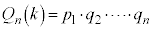
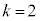 (�Ԃ�2��ڂɎ��o��)�Ȃ�A
(�Ԃ�2��ڂɎ��o��)�Ȃ�A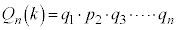
�E�E�E�E�E�E
�E�E�E�E�E�E
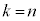 (�Ԃ�n��ڂɎ��o��)�Ȃ�A
(�Ԃ�n��ڂɎ��o��)�Ȃ�A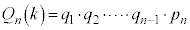
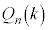 �̕����
�̕����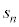 �C���q��
�C���q��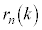 �Ə����A
�Ə����A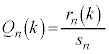 �Ƃ��āA��L������ƁA�e�Ƃɐԍ����킹���ʂ̌���
�Ƃ��āA��L������ƁA�e�Ƃɐԍ����킹���ʂ̌���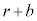 ����1��������n��ڂ�
����1��������n��ڂ�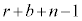 �ƂȂ�A
�ƂȂ�A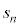 �́A�e��̋ʂ̌��̐ςƂȂ�A
�́A�e��̋ʂ̌��̐ςƂȂ�A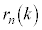 �́A
�́A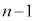 ��ڂ܂łɁA�ԋʂ�1��A���ʂ�
��ڂ܂łɁA�ԋʂ�1��A���ʂ�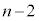 ����o���Ar��
����o���Ar��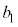 �`
�`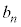 (�r���A�ǂ���1��
(�r���A�ǂ���1��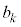 �������邱�Ƃɒ���)�̐ςƂȂ�̂ł����A���ʂ̌��̐ςɂ��ẮA���ʂ�b����
�������邱�Ƃɒ���)�̐ςƂȂ�̂ł����A���ʂ̌��̐ςɂ��ẮA���ʂ�b����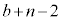 �܂�1��������̂ŁAb����
�܂�1��������̂ŁAb����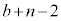 �܂ł̐ςɂȂ�܂��B�܂�A
�܂ł̐ςɂȂ�܂��B�܂�A����āA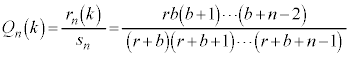 �@����B
�@����B
�A�C�B���A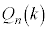 ��k�ɂ��܂���B
��k�ɂ��܂���B ���D��L�ł́A������₷���悤�ɁA�ԋʂ����o���ꍇ�ƍ��ʂ����o���ꍇ���Ē��J�ɏ����܂������A�������ł́A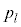 �C
�C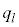 ���Ƃ���
���Ƃ���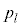 �Ə����āAk��ڂ����ԋʂ����o���A����ȊO�͍��ʂ����o���m���Ƃ��A
�Ə����āAk��ڂ����ԋʂ����o���A����ȊO�͍��ʂ����o���m���Ƃ��A �Ƃ��Ă��܂��̂łȂ��ƁA���Ă������X�y�[�X������Ȃ��Ȃ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 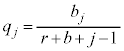
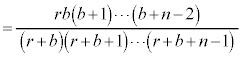
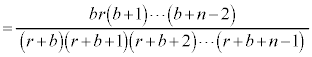
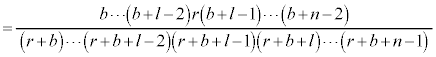
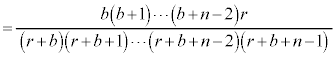
 �Ƃ��āA��L������ƁA�e�Ƃɐԍ����킹���ʂ̌���
�Ƃ��āA��L������ƁA�e�Ƃɐԍ����킹���ʂ̌���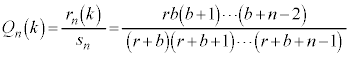 �@����B
�@����B