早稲田大学基幹・創造・先進理工学部2023年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] nを自然数として、整式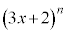 を
を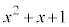 で割った余りを
で割った余りを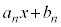 とおく。以下の問に答えよ。
とおく。以下の問に答えよ。
(2) 全てのnに対して、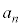 と
と は7で割り切れないことを示せ。
は7で割り切れないことを示せ。 (3) 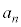 と
と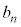 を
を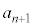 と
と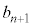 で表し、全てのnに対して、2つの整数
で表し、全てのnに対して、2つの整数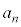 と
と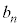 は互いに素であることを示せ。
は互いに素であることを示せ。 [解答へ]
[2] 赤玉と黒玉が入っている袋の中から無作為に玉を1つ取り出し、取り出した玉を袋に戻した上で、取り出した玉と同じ色の玉をもう1つ袋に入れる操作を繰り返す。以下の問に答えよ。
(1) 初めに袋の中に赤玉が1個、黒玉が1個入っているとする。n回の操作を行ったとき、赤玉をちょうどk回取り出す確率を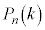 (
(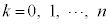 )とする。
)とする。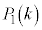 と
と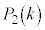 を求め、さらに
を求め、さらに を求めよ。
を求めよ。 (2) 初めに袋の中に赤玉がr個、黒玉がb個(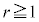 ,
,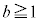 )入っているとする。n回の操作を行ったとき、k回目に赤玉が、それ以外ではすべて黒玉が取り出される確率を
)入っているとする。n回の操作を行ったとき、k回目に赤玉が、それ以外ではすべて黒玉が取り出される確率を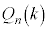 (
(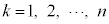 )とする。
)とする。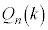 はkによらないことを示せ。
はkによらないことを示せ。 [解答へ]
[3] 実数xに対して関数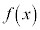 を
を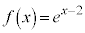 で定め、正の実数xに対して関数
で定め、正の実数xに対して関数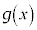 を
を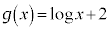 で定める。また、
で定める。また、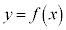 ,
,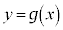 のグラフをそれぞれ
のグラフをそれぞれ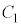 ,
,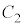 とする。以下の問に答えよ。
とする。以下の問に答えよ。
(1) 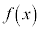 と
と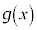 がそれぞれ互いの逆関数であることを示せ。
がそれぞれ互いの逆関数であることを示せ。 (2) 直線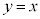 と
と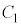 が2点で交わることを示せ。ただし、必要なら
が2点で交わることを示せ。ただし、必要なら を証明しないで用いてよい。
を証明しないで用いてよい。 (3) 直線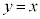 と
と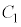 との2つの交点のx座標をα,βとする。ただし、
との2つの交点のx座標をα,βとする。ただし、 とする。直線
とする。直線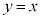 と
と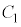 ,
,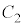 をすべて同じxy平面上に図示せよ。
をすべて同じxy平面上に図示せよ。 (4) 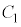 と
と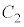 で囲まれる図形の面積を(3)のα,βの多項式で表せ。
で囲まれる図形の面積を(3)のα,βの多項式で表せ。 [解答へ]
[4] 複素数平面上に2点A(1),B(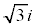 )がある。ただし、iは虚数単位である。複素数zに対し、
)がある。ただし、iは虚数単位である。複素数zに対し、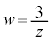 で表される点wを考える。以下の問に答えよ。
で表される点wを考える。以下の問に答えよ。
(1) 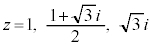 のときのwをそれぞれ計算せよ。
のときのwをそれぞれ計算せよ。 (2) 実数t に対し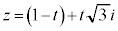 とする。
とする。 について、
について、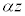 の実部を求め、さらに
の実部を求め、さらに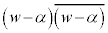 を求めよ。
を求めよ。 (3) wと原点を結んでできる線分Lを考える。zが線分AB上を動くとき、線分Lが通過する範囲を図示し、その面積を求めよ。
[解答へ]
[5] xyz空間において、3点A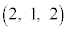 ,B
,B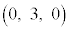 ,C
,C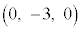 を頂点とする三角形ABCを考える。以下の問に答えよ。
を頂点とする三角形ABCを考える。以下の問に答えよ。
(1) 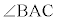 を求めよ。
を求めよ。 (2) 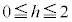 に対し、線分AB,ACと平面
に対し、線分AB,ACと平面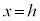 との交点をそれぞれP,Qとする。点P,Qの座標を求めよ。
との交点をそれぞれP,Qとする。点P,Qの座標を求めよ。 (3) 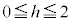 に対し、点
に対し、点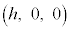 と線分PQの距離をhで表せ。ただし、点と線分の距離とは、点と線分上の点の距離の最小値である。
と線分PQの距離をhで表せ。ただし、点と線分の距離とは、点と線分上の点の距離の最小値である。 (4) 三角形ABCをx軸のまわりに1回転させ、そのときに三角形が通過する点全体からなる立体の体積を求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。