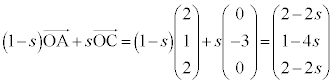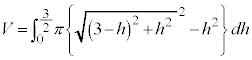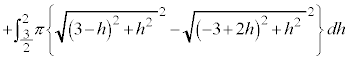���嗝�H���w'23�N[5]
xyz��Ԃɂ����āA3�_A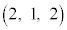 �CB
�CB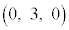 �CC
�CC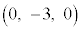 �_�Ƃ���O�p�`ABC���l����B�ȉ��̖�ɓ�����B
�_�Ƃ���O�p�`ABC���l����B�ȉ��̖�ɓ�����B
(1) 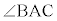 �����߂�B
�����߂�B (2) 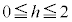 �ɑ��A����AB�CAC�ƕ���
�ɑ��A����AB�CAC�ƕ���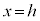 �Ƃ̌�_�����ꂼ��P�CQ�Ƃ���B�_P�CQ�̍��W�����߂�B
�Ƃ̌�_�����ꂼ��P�CQ�Ƃ���B�_P�CQ�̍��W�����߂�B (3) 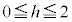 �ɑ��A�_
�ɑ��A�_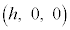 �Ɛ���PQ�̋�����h�ŕ\���B�������A�_�Ɛ����̋����Ƃ́A�_�Ɛ�����̓_�̋����̍ŏ��l�ł���B
�Ɛ���PQ�̋�����h�ŕ\���B�������A�_�Ɛ����̋����Ƃ́A�_�Ɛ�����̓_�̋����̍ŏ��l�ł���B (4) �O�p�`ABC��x���̂܂���1��]�����A���̂Ƃ��ɎO�p�`���ʉ߂���_�S�̂���Ȃ闧�̂̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�U���ɏ���đf���Ɍv�Z���čs���A�v�Z���債�����Ƃ͂Ȃ��A�m���ɓ��_���������ł��B
(1) 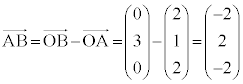 �C
�C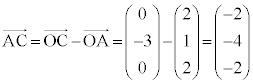 �@����@
�@����@
 (2) ����AB��̓_�́At ��
(2) ����AB��̓_�́At ��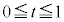 ���������Ƃ��āA
���������Ƃ��āA����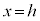 �Ƃ̌�_P�́A
�Ƃ̌�_P�́A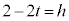 �Ƃ��āA
�Ƃ��āA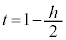 �C
�C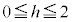 ���
���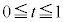 �ł��B
�ł��B
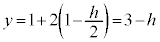 �C
�C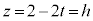 ���AP
���AP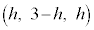 ......[��]����AC��̓_�́As��
......[��]����AC��̓_�́As��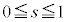 ���������Ƃ��āA
���������Ƃ��āA
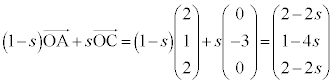
����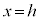 �Ƃ̌�_Q�́A
�Ƃ̌�_Q�́A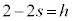 ���A
���A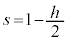 �C
�C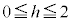 ���
���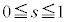 �ł��B
�ł��B
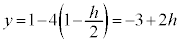 �C
�C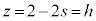 ���AQ
���AQ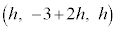 ......[��]
......[��]
(3) P�CQ�͂Ƃ��ɕ���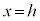 ��̓_�ł����Az���W�͂Ƃ���x���W�Ɠ�����h�Ȃ̂ŁA
��̓_�ł����Az���W�͂Ƃ���x���W�Ɠ�����h�Ȃ̂ŁA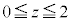 �͈̔͂ɂ���܂��B����PQ (
�͈̔͂ɂ���܂��B����PQ (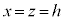 )��y���ƕ��s�ŁA�_H
)��y���ƕ��s�ŁA�_H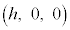 �Ƃ̋�����h�ł����A����PQ�Ƃ̋����̏ꍇ�ɂ́AH�������PQ�ɉ��낵�������̑�R���A����PQ�̒��ɗ��邩�A�Ƃ������Ƃ����ɂȂ�܂��BR�́Azx����(
�Ƃ̋�����h�ł����A����PQ�Ƃ̋����̏ꍇ�ɂ́AH�������PQ�ɉ��낵�������̑�R���A����PQ�̒��ɗ��邩�A�Ƃ������Ƃ����ɂȂ�܂��BR�́Azx����(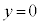 )��ɂ���̂ŁA(2)�̌��ʂ��g���āAP��Q��y���W�̕����ׂ܂��B
)��ɂ���̂ŁA(2)�̌��ʂ��g���āAP��Q��y���W�̕����ׂ܂��B P��y���W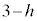 �́A
�́A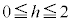 ���A
���A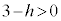 �ł��BQ��y���W
�ł��BQ��y���W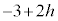 �́A
�́A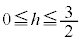 �̂Ƃ��ɂ�
�̂Ƃ��ɂ�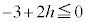 �ł����A
�ł����A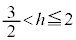 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A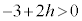 �ɂȂ��Ă��܂��܂��B
�ɂȂ��Ă��܂��܂��B
�܂�AH�������PQ�ɐ��������낷�Ƃ��A�����̑�R�́A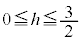 �̂Ƃ��ɂ́A����PQ��ɗ��܂����A
�̂Ƃ��ɂ́A����PQ��ɗ��܂����A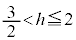 �ɂȂ�ƁAP��Q��
�ɂȂ�ƁAP��Q��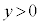 ���ɗ���̂ŁAR�͐���PQ��ɗ��܂���B���̂Ƃ��AP��Q��y���W���ׂ�ƁA
���ɗ���̂ŁAR�͐���PQ��ɗ��܂���B���̂Ƃ��AP��Q��y���W���ׂ�ƁA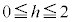 �ł���A
�ł���A �Ȃ̂ŁA
P�CQ��y���W����v����Ƃ�(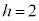 �̂Ƃ��AP�CQ��A�Ɉ�v)���܂߂āAP��y���W�̕����傫���B�@���(��)
�̂Ƃ��AP�CQ��A�Ɉ�v)���܂߂āAP��y���W�̕����傫���B�@���(��) ���Ƃ��킩��܂��B�܂�AH�Ɛ���PQ�Ƃ̋����́AH��Q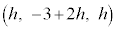 �Ƃ̋���
�Ƃ̋��� 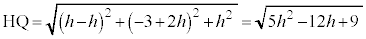 �@����@
�@����@�ɂȂ�܂��B
�ȏ���A�_H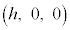 �Ɛ���PQ�̋����́A
�Ɛ���PQ�̋����́A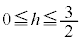 �̂Ƃ���h�C
�̂Ƃ���h�C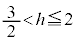 �̂Ƃ���
�̂Ƃ���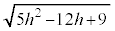 ......[��]
......[��]
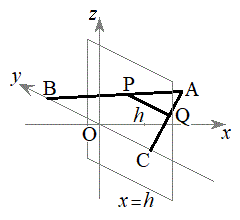
(4) ����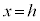 �ŎO�p�`ABC���Ɛ���PQ�ɂȂ�܂��B�O�p�`ABC��x���̎���ɉ�]�����Ăł��闧�̂�
�ŎO�p�`ABC���Ɛ���PQ�ɂȂ�܂��B�O�p�`ABC��x���̎���ɉ�]�����Ăł��闧�̂�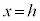 �Ő����Ƃ��̒f�ʂ́A����PQ��x���̎���ɉ�]�����Ăł���}�`�ɂȂ�܂��B
�Ő����Ƃ��̒f�ʂ́A����PQ��x���̎���ɉ�]�����Ăł���}�`�ɂȂ�܂��B ���̐}�`�́A����PQ��̓_�̒��ōł�H�ɋ߂��_��x���̎���ɉ�]���Ăł���~��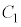 �ƁA����PQ��̓_�ōł�H���牓���_��x���̎���ɉ�]���Ăł���~��
�ƁA����PQ��̓_�ōł�H���牓���_��x���̎���ɉ�]���Ăł���~��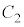 �ɋ��܂ꂽ�}�`�ɂȂ�܂��B(3)��(��)���A����PQ��̓_�ōł�H���牓���_�́A����PQ�̒[�_P�ł��BH��P
�ɋ��܂ꂽ�}�`�ɂȂ�܂��B(3)��(��)���A����PQ��̓_�ōł�H���牓���_�́A����PQ�̒[�_P�ł��BH��P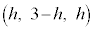 �Ƃ̋����́A
�Ƃ̋����́A �ł��B���ꂪ�~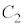 �̔��a�ɂȂ�܂��B
�̔��a�ɂȂ�܂��B
�~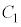 �̔��a�́A
�̔��a�́A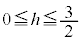 �̂Ƃ�h�C
�̂Ƃ�h�C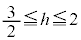 �̂Ƃ�
�̂Ƃ�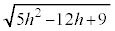 (
(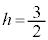 �̂Ƃ�
�̂Ƃ�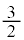 )�ł��BA��x���W��2�ł���AB�CC��x���W��0�Ȃ̂ŁA�O�p�`ABC��
)�ł��BA��x���W��2�ł���AB�CC��x���W��0�Ȃ̂ŁA�O�p�`ABC��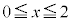 �͈̔͂ɑ��݂��܂��B
�͈̔͂ɑ��݂��܂��B
����āA�O�p�`ABC��x���̂܂���1��]�������Ƃ��ɎO�p�`���ʉ߂���_�S�̂���Ȃ闧�̂̑̐�V�́A�@���A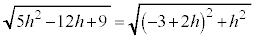 �Ȃ̂ŁA
�Ȃ̂ŁA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 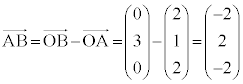 �C
�C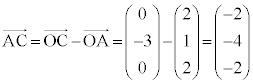 �@����@
�@����@