���嗝�H���w'23�N[3]
����x�ɑ��Ċ�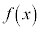 ��
��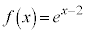 �Œ�߁A���̎���x�ɑ��Ċ�
�Œ�߁A���̎���x�ɑ��Ċ�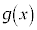 ��
��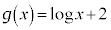 �Œ�߂�B�܂��A
�Œ�߂�B�܂��A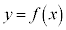 �C
�C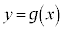 �̃O���t�����ꂼ��
�̃O���t�����ꂼ��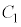 �C
�C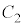 �Ƃ���B�ȉ��̖�ɓ�����B
�Ƃ���B�ȉ��̖�ɓ�����B
(1) 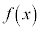 ��
��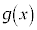 �����ꂼ��݂��̋t���ł��邱�Ƃ������B
�����ꂼ��݂��̋t���ł��邱�Ƃ������B (2) ����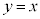 ��
��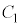 ��2�_�Ō���邱�Ƃ������B�������A�K�v�Ȃ�
��2�_�Ō���邱�Ƃ������B�������A�K�v�Ȃ�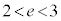 ���ؖ����Ȃ��ŗp���Ă悢�B
���ؖ����Ȃ��ŗp���Ă悢�B (3) ����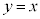 ��
��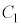 �Ƃ�2�̌�_��x���W��α�Cβ�Ƃ���B�������A
�Ƃ�2�̌�_��x���W��α�Cβ�Ƃ���B�������A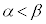 �Ƃ���B����
�Ƃ���B����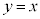 ��
��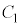 �C
�C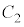 �����ׂē���xy���ʏ�ɐ}������B
�����ׂē���xy���ʏ�ɐ}������B (4) 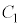 ��
��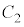 �ň͂܂��}�`�̖ʐς�(3)��α�Cβ�̑������ŕ\���B
�ň͂܂��}�`�̖ʐς�(3)��α�Cβ�̑������ŕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��N�Ɣ�r���Čy�����ł��B
(1) 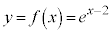 (�w�������Q��)�ɂ����āAx��y�����ւ��A
(�w�������Q��)�ɂ����āAx��y�����ւ��A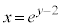 ��y�ɂ��ĉ����܂��Bx�́A
��y�ɂ��ĉ����܂��Bx�́A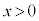 �ƂȂ�C�ӂ̎������Ƃ蓾�܂��B
�ƂȂ�C�ӂ̎������Ƃ蓾�܂��B 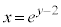 ���ӂ��ΐ������ƁA
���ӂ��ΐ������ƁA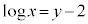 �@��
�@�� 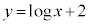
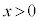 �ƂȂ�C�ӂ̎���x�ɑ��āA����1��
�ƂȂ�C�ӂ̎���x�ɑ��āA����1��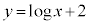 ���Ή����܂��B����āA
���Ή����܂��B����āA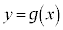 ��
��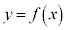 ���t���ł��B���̂Ƃ��A
���t���ł��B���̂Ƃ��A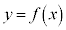 ��
��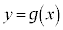 �̋t���ł��B
�̋t���ł��B
(2) 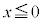 �ɂ�����
�ɂ�����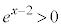 �Ȃ̂ŁA����
�Ȃ̂ŁA����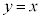 ��
��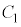 �F
�F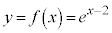 ��
��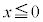 �ɂ����Č�_�������܂���B
�ɂ����Č�_�������܂���B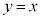 ��
��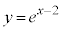 ��A������ƁA
��A������ƁA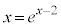
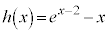 �Ƃ����ƁA
�Ƃ����ƁA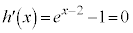 �Ƃ���ƁA
�Ƃ���ƁA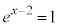 �@��
�@�� 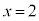
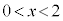 �ɂ����āA
�ɂ����āA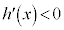 ���(���̑������Q��)�A
���(���̑������Q��)�A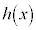 ���P�������ł��B
���P�������ł��B
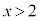 �ɂ����āA
�ɂ����āA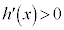 ���A
���A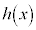 �͒P�������ł��B
�͒P�������ł��B
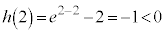
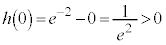 �C
�C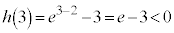 �C
�C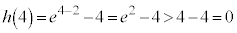
����āA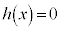 �C�����A
�C�����A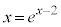 �́A
�́A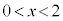 �͈̔͂�1���A
�͈̔͂�1���A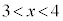 �͈̔͂�1��������(���Ԓl�̒藝���Q��)�A
�͈̔͂�1��������(���Ԓl�̒藝���Q��)�A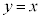 ��
��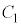 ��2�_�Ō����܂��B
��2�_�Ō����܂��B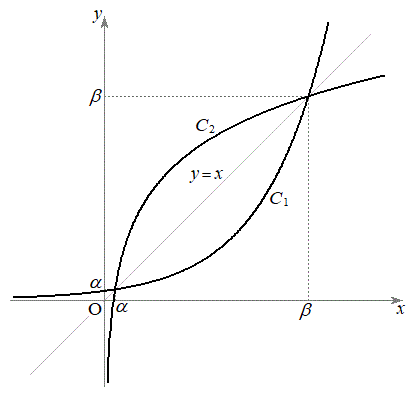
(3) (2)��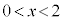 �͈̔͂̉���α�C
�͈̔͂̉���α�C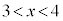 �͈̔͂̉���β�Ƃ��܂��Bα�Cβ���A
�͈̔͂̉���β�Ƃ��܂��Bα�Cβ���A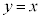 ��
��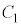 �̌�_��x���W��^���܂��B
�̌�_��x���W��^���܂��B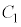 ��
��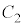 ��(1)���A
��(1)���A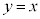 �Ɋւ��đΏ̂ł��B
�Ɋւ��đΏ̂ł��B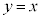 ��
��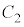 ��
��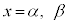 �ɂ����Č����܂��B
�ɂ����Č����܂��B 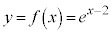 �͒P�������Ȋ���
�͒P�������Ȋ���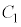 �͉��ɓʁA
�͉��ɓʁA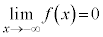 �C
�C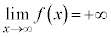 �C
�C
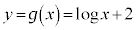 �͒P�������Ȋ���
�͒P�������Ȋ���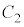 �͏�ɓʁA
�͏�ɓʁA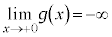 �C
�C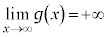
����āA����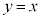 ��
��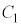 �C
�C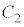 ��}������ƁA�E�}�B
��}������ƁA�E�}�B
(4) α�Cβ�́A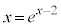 �̉��Ȃ̂ŁA
�̉��Ȃ̂ŁA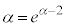 �C
�C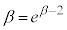 �@����@�@�����܂��B
�@����@�@�����܂��B
�܂��A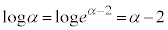 �C
�C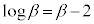 �@����A(3)�̃O���t���A
�@����A(3)�̃O���t���A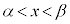 �ɂ����āA
�ɂ����āA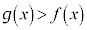 �C����āA
�C����āA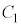 ��
��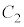 �ň͂܂��}�`�̖ʐ�S�́A
�ň͂܂��}�`�̖ʐ�S�́A 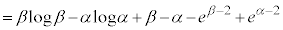
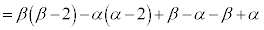 �@(�� �@�C�A)
�@(�� �@�C�A)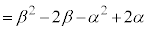 �@......[��]
�@......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B