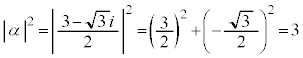���嗝�H���w'23�N[4]
���f�����ʏ��2�_A(1)�CB(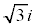 )������B�������Ai�͋����P�ʂł���B���f��z�ɑ��A
)������B�������Ai�͋����P�ʂł���B���f��z�ɑ��A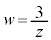 �ŕ\�����_w���l����B�ȉ��̖�ɓ�����B
�ŕ\�����_w���l����B�ȉ��̖�ɓ�����B
(1) 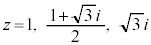 �̂Ƃ���w�����ꂼ��v�Z����B
�̂Ƃ���w�����ꂼ��v�Z����B (2) ����t �ɑ�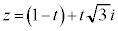 �Ƃ���B
�Ƃ���B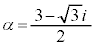 �ɂ��āA
�ɂ��āA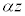 �̎��������߁A�����
�̎��������߁A����� �����߂�B
�����߂�B (3) w�ƌ��_������łł������L���l����Bz������AB����Ƃ��A����L���ʉ߂���͈͂�}�����A���̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�U�������܂�ɐe�����āA�r���ʼn�������Ă���̂��킩��Ȃ��Ȃ�܂����A�Ō��1�{�̐��ɂȂ���܂��B�Ȃ��A���f���̐}�`�I���p���Q�Ƃ��Ă��������B
(1) 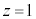 �̂Ƃ��A
�̂Ƃ��A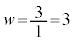 ......[��]
......[��] 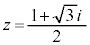 �̂Ƃ��A
�̂Ƃ��A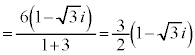 ......[��]
......[��]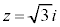 �̂Ƃ��A
�̂Ƃ��A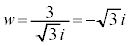 ......[��]
......[��]
(2) 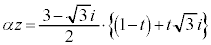
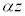 ��������
��������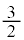 ......[��]�@����@
......[��]�@����@
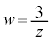 ���A
���A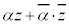 ��
�� �̎�����2�{�ŁA�@���A
�̎�����2�{�ŁA�@���A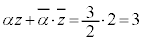 �C���ǁA
�C���ǁA����āA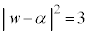 �C�܂�Aw�́Aα�𒆐S�Ƃ��Ĕ��a
�C�܂�Aw�́Aα�𒆐S�Ƃ��Ĕ��a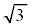 �̉~����̓_�ł��B
�̉~����̓_�ł��B 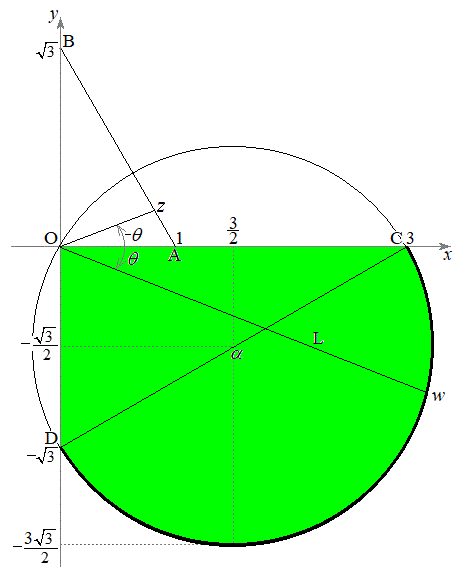
(3) ����AB��̓_�́At ��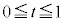 ���������Ƃ��āA
���������Ƃ��āA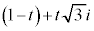 �ƕ\����܂��B�܂��蕶����z�ł��B�A���A
�ƕ\����܂��B�܂��蕶����z�ł��B�A���A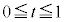 �Ƃ����������t���܂��B
�Ƃ����������t���܂��B w�ƌ��_������łł������L��x���Ƃ��Ȃ��p���v���𐳂̕����Ƃ���θ�Ƃ���ƁA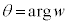 �ł�(�Ίp���Q��)�B
�ł�(�Ίp���Q��)�B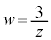 ���A
���A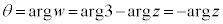 t ��0����1�܂ŕς��ƁA
t ��0����1�܂ŕς��ƁA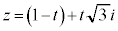 �́A1����
�́A1����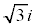 �܂ŕς��Az�̕\���_��A����B�܂œ����܂��B���̂Ƃ��A
�܂ŕς��Az�̕\���_��A����B�܂œ����܂��B���̂Ƃ��A ��0����
��0����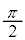 �܂ŕς��܂��B
�܂ŕς��܂��B
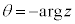 �́A0����
�́A0����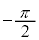 �܂ŕς��Aw�́Aα�𒆐S�Ƃ��Ĕ��a
�܂ŕς��Aw�́Aα�𒆐S�Ƃ��Ĕ��a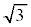 �̉~����̓_�Ȃ̂ŁAC(3)�AD(
�̉~����̓_�Ȃ̂ŁAC(3)�AD(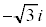 )�Ƃ��āA����L�́AOC���玞�v����OD�܂œ����܂��BC��D�̒��_��α�Ȃ̂ŁAC��D�͉~�̒��a�̗��[�ł��B����āA����L���ʉ߂���͈͂�}������ƉE�}���ΐF���F���B���̖ʐς́A��OCD�̖ʐςƔ��a
)�Ƃ��āA����L�́AOC���玞�v����OD�܂œ����܂��BC��D�̒��_��α�Ȃ̂ŁAC��D�͉~�̒��a�̗��[�ł��B����āA����L���ʉ߂���͈͂�}������ƉE�}���ΐF���F���B���̖ʐς́A��OCD�̖ʐςƔ��a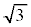 �̔��~�̖ʐς̘a�ŁA
�̔��~�̖ʐς̘a�ŁA 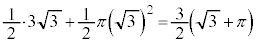 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  ......[��]
......[��]