���嗝�H���w'25�N[2]
xy���ʏ�ŁA�A���s����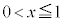 �C
�C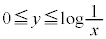 �Œ�܂�̈��y����
�Œ�܂�̈��y���� �̕��������킹���}�`��D�Ƃ���BD�Ɋ܂܂��O�p�`�̖ʐς̍ő�l�����߂�B
�̕��������킹���}�`��D�Ƃ���BD�Ɋ܂܂��O�p�`�̖ʐς̍ő�l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
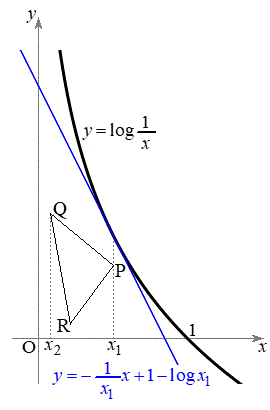
���@���Ƃ͌����܂��A�uD�Ɋ܂܂��O�p�`�v�Ƃ����ݒ�ɔY�܂���܂��B�ȉ��ł́AD�Ɋ܂܂��O�p�`���̂��̂̍ő���l����̂ł͂Ȃ��AD�Ɋ܂܂��O�p�`���A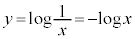 �̐ڐ���x���Ay���ň͂ގO�p�`T�Ɋ܂܂�邱�Ƃ���AT�̖ʐς̍ő���l���AT�ő�̂Ƃ��̎O�p�`��D�Ɋ܂܂�邱�Ƃ��m�F���܂��B
�̐ڐ���x���Ay���ň͂ގO�p�`T�Ɋ܂܂�邱�Ƃ���AT�̖ʐς̍ő���l���AT�ő�̂Ƃ��̎O�p�`��D�Ɋ܂܂�邱�Ƃ��m�F���܂��B
D�̋��E����1�́A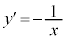 �@����@
�@����@
�ł��B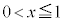 ���A
���A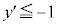 �̂Ƃ�
�̂Ƃ�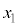 �@����A
�@����A
�ł��B
D���ɈقȂ�3�_���Ƃ�A���̒���x���W���ő�ƂȂ�_�A2�_����ꍇ�ɂ�y���W���傫�����̓_��P�A����1�_��R�Ƃ��A����x���W��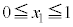 (
(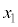 �ł�)�Ƃ��܂��B���̂Ƃ��A�c��1�_�A�����A����x���W
�ł�)�Ƃ��܂��B���̂Ƃ��A�c��1�_�A�����A����x���W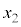 ��
��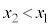 �ƂȂ�_��Q�Ƃ��܂��B3�_��x���W���������
�ƂȂ�_��Q�Ƃ��܂��B3�_��x���W���������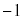 �A����
�A����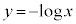 �ƂȂ邱�Ƃ͂���܂���B�O�p�`���ł��Ȃ��Ȃ��Ă��܂�����ł��B
�ƂȂ邱�Ƃ͂���܂���B�O�p�`���ł��Ȃ��Ȃ��Ă��܂�����ł��B
x���W��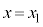 �ƂȂ�_��P�����̂Ƃ��͎c��2�_�̂����AP�ƌ���łł��钼���̌X���̏�������(�X�����Ƃ��ɕ��̏ꍇ�́A�X���̐�Βl���傫����)������PQ�ƂȂ�悤�ɁA2�_��Q�CR�Ƃ��܂��B��͂�A�O�p�`���ł��Ȃ��Ȃ�̂ŁAPQ��PR�̌X������v���邱�Ƃ͂���܂���B
�ƂȂ�_��P�����̂Ƃ��͎c��2�_�̂����AP�ƌ���łł��钼���̌X���̏�������(�X�����Ƃ��ɕ��̏ꍇ�́A�X���̐�Βl���傫����)������PQ�ƂȂ�悤�ɁA2�_��Q�CR�Ƃ��܂��B��͂�A�O�p�`���ł��Ȃ��Ȃ�̂ŁAPQ��PR�̌X������v���邱�Ƃ͂���܂���B
�����ŁAR������PQ�̉����ɂ��邱�Ƃɒ��ӂ��āA����PQ�̌X����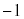 �ȏォ�ǂ�����2�ʂ�ɏꍇ�������܂��B
�ȏォ�ǂ�����2�ʂ�ɏꍇ�������܂��B
 �E����PQ�̌X����
�E����PQ�̌X���� �ȏ�̏ꍇ(�E��}�̏ꍇ)
�ȏ�̏ꍇ(�E��}�̏ꍇ)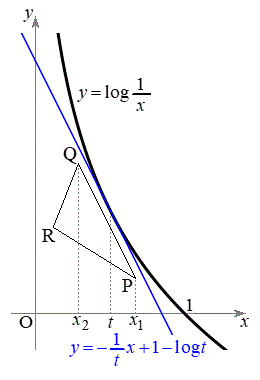 �E����PQ�̌X����
�E����PQ�̌X���� ��菬�����ꍇ(�E���}�̏ꍇ)
��菬�����ꍇ(�E���}�̏ꍇ)�Ȑ�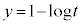 ��
��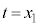 �ɂ�����ڐ�m�̌X��
�ɂ�����ڐ�m�̌X�� (�A���
(�A���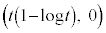 )������PQ�̌X���Ɉ�v����t ������(����PQ�ƕ��s�Ȑڐ�������)���܂��B�����ڐ�m��
)������PQ�̌X���Ɉ�v����t ������(����PQ�ƕ��s�Ȑڐ�������)���܂��B�����ڐ�m��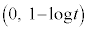 ��ʂ�̂ŁA
��ʂ�̂ŁA 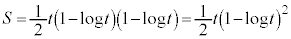 �@����B
�@����B�ł��B����PQ���ڐ�m�Ɉ�v���邱�Ƃ͂���܂����A����PQ���ڐ�m������ɗ��邱�Ƃ͂���܂���B��PQR��D�Ɋ܂܂�Ȃ��Ȃ�܂��B�܂�A����PQ�͐ڐ�m���牺���ɂ���܂��BR�́A����PQ�̉����ɂ���܂��B�܂�A��PQR�́A�ڐ�m��x���Ay���ň͂܂��O�p�`T�Ɋ܂܂�܂��B
�ȏ���A��PQR�́A��v����ꍇ���܂߁A�Ȑ�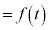 ��
��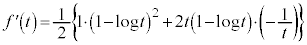 (
(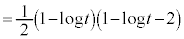 )�ɂ�����ڐ��F
)�ɂ�����ڐ��F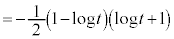 �@����B�@�̂ǂꂩ��x���Cy���Ƃň͂܂��O�p�`T�Ɋ܂܂�܂��B
�@����B�@�̂ǂꂩ��x���Cy���Ƃň͂܂��O�p�`T�Ɋ܂܂�܂��B
�B��x���Ƃ̌�_��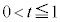 �Ƃ��āA
�Ƃ��āA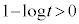 �C
�C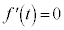
�B��y���Ƃ̌�_�́A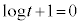 �Ƃ��āA
�Ƃ��āA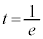
��PQR�̖ʐς́AD����3�_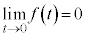 �C
�C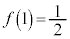 �C
�C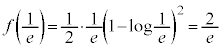 �@����C�@�ō����O�p�`T�̖ʐ�S�ȉ��ɂȂ�܂��BS�́A
�@����C�@�ō����O�p�`T�̖ʐ�S�ȉ��ɂȂ�܂��BS�́A
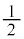 �ɂ�����
�ɂ�����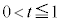 ���A
���A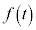 �Ƃ���ƁA
�Ƃ���ƁA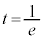 �C
�C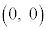
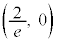 �C
�C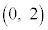 �C
�C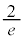 ���A
���A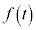 �������\�͈ȉ��̂悤�ɂȂ�܂��B
�������\�͈ȉ��̂悤�ɂȂ�܂��B
�����\���A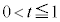 �ɂ����āA
�ɂ����āA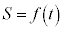 ��
��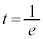 �̂Ƃ��ɍő�ɂȂ�܂����A���̂Ƃ��A�C���O�p�`T��3���_�́A
�̂Ƃ��ɍő�ɂȂ�܂����A���̂Ƃ��A�C���O�p�`T��3���_�́A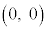 �C
�C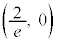 �C
�C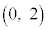 �ł���A���̎O�p�`��D�Ɋ܂܂�Ă��܂��B����āAD�Ɋ܂܂��O�p�`�̖ʐς̍ő�l�́A
�ł���A���̎O�p�`��D�Ɋ܂܂�Ă��܂��B����āAD�Ɋ܂܂��O�p�`�̖ʐς̍ő�l�́A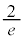 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B