早稲田大学基幹・創造・先進理工学部2025年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 複素数平面上で、複素数zが円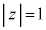 の上を動くとき、
の上を動くとき、
を満たす点wの軌跡をCとする。次の問に答えよ。
(1) Cはどのような図形か。複素数平面上に図示せよ。
(2) Cと円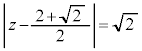 の共有点を求めよ。
の共有点を求めよ。 (3) Cで囲まれる領域と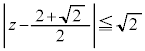 の表す領域の共通部分の面積を求めよ。
の表す領域の共通部分の面積を求めよ。 [解答へ]
[2] xy平面上で、連立不等式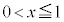 ,
,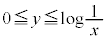 で定まる領域とy軸の
で定まる領域とy軸の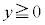 の部分を合わせた図形をDとする。Dに含まれる三角形の面積の最大値を求めよ。
の部分を合わせた図形をDとする。Dに含まれる三角形の面積の最大値を求めよ。
[解答へ]
[3] 1からnまでの異なる自然数が1つずつ書かれたn枚のカードが一列に並んでいる。このとき、どのカードも現在とは異なる位置に移動するように並べ替えてできる順列の総数を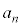 で表し、並べ方の総数
で表し、並べ方の総数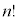 に占める
に占める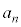 の割合を
の割合を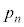 で表す。例えば、
で表す。例えば、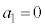 ,
,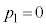 ,
,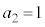 ,
,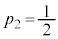 ,
,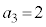 ,
,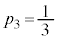 である。次の問に答えよ。
である。次の問に答えよ。
(1) 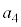 の値を求めよ。
の値を求めよ。 (3) 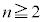 のとき、
のとき、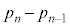 をnを用いて表せ。
をnを用いて表せ。 [解答へ]
[4] 空間内に原点Oを中心とする半径rの球面Sがある。さらに、半径が1,2,3の球面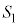 ,
,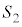 ,
,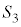 があり、これら4つの球面のうちどの2つの球面も互いに外接している。
があり、これら4つの球面のうちどの2つの球面も互いに外接している。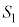 ,
,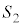 ,
,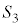 の中心を順に
の中心を順に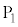 ,
,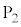 ,
,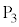 とし、O,
とし、O,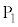 ,
,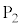 ,
,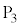 は同一平面上にないとする。さらに、球面Sが球面
は同一平面上にないとする。さらに、球面Sが球面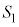 ,
,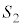 ,
,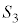 と接する3つの点と、
と接する3つの点と、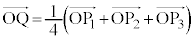 により定まる点Qは、同一平面上にあるとする。次の問に答えよ。
により定まる点Qは、同一平面上にあるとする。次の問に答えよ。
(1) rの値を求めよ。
(2) 四面体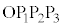 の体積を求めよ。
の体積を求めよ。 [解答へ]
[5] xy平面上の曲線C: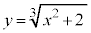 を考え、C上の
を考え、C上の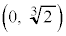 以外の点P
以外の点P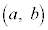 における接線を
における接線を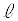 :
: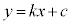 と表す。Cと
と表す。Cと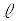 の方程式からxを消去して得られるyについての3次方程式
の方程式からxを消去して得られるyについての3次方程式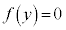 はbを重解としてもつので、もう1つの解を
はbを重解としてもつので、もう1つの解を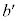 とする。ただし、bが3重解のときは
とする。ただし、bが3重解のときは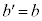 とみなす。次の問に答えよ。
とみなす。次の問に答えよ。
(1) 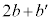 をkのみの分数式で表せ。
をkのみの分数式で表せ。 (2) 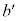 をbのみの分数式で表せ。
をbのみの分数式で表せ。 (3) Cと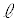 の共有点で、そのy座標が
の共有点で、そのy座標が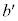 であるものを
であるものを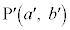 とする。aとbが有理数ならば、
とする。aとbが有理数ならば、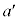 と
と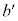 も有理数であることを示せ。
も有理数であることを示せ。 (4) bが奇数p,qと負でない整数rを用いて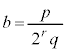 で与えられるとする。有理数
で与えられるとする。有理数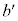 を奇数
を奇数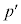 ,
,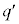 と整数sを用いて
と整数sを用いて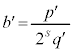 と表すとき、sをrの式で表せ。
と表すとき、sをrの式で表せ。 (5) P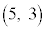 が曲線C上の点であることを利用して、C上にx座標とy座標がともに有理数であるような点が無数に存在することを示せ。
が曲線C上の点であることを利用して、C上にx座標とy座標がともに有理数であるような点が無数に存在することを示せ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 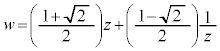
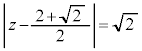 の共有点を求めよ。
の共有点を求めよ。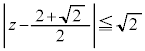 の表す領域の共通部分の面積を求めよ。
の表す領域の共通部分の面積を求めよ。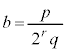 で与えられるとする。有理数
で与えられるとする。有理数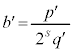 と表すとき、sをrの式で表せ。
と表すとき、sをrの式で表せ。