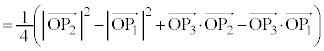���嗝�H���w'25�N[4]
��ԓ��Ɍ��_O�𒆐S�Ƃ��锼�ar�̋���S������B����ɁA���a��1�C2�C3�̋���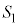 �C
�C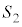 �C
�C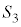 ������A�����4�̋��ʂ̂����ǂ�2�̋��ʂ��݂��ɊO�ڂ��Ă���B
������A�����4�̋��ʂ̂����ǂ�2�̋��ʂ��݂��ɊO�ڂ��Ă���B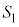 �C
�C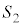 �C
�C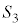 �̒��S������
�̒��S������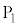 �C
�C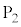 �C
�C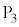 �Ƃ��AO�C
�Ƃ��AO�C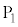 �C
�C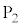 �C
�C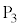 �͓��ꕽ�ʏ�ɂȂ��Ƃ���B����ɁA����S������
�͓��ꕽ�ʏ�ɂȂ��Ƃ���B����ɁA����S������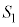 �C
�C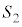 �C
�C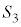 �Ɛڂ���3�̓_�ƁA
�Ɛڂ���3�̓_�ƁA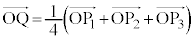 �ɂ���܂�_Q�́A���ꕽ�ʏ�ɂ���Ƃ���B���̖�ɓ�����B
�ɂ���܂�_Q�́A���ꕽ�ʏ�ɂ���Ƃ���B���̖�ɓ�����B
(1) r�̒l�����߂�B
(2) �l�ʑ�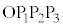 �̑̐ς����߂�B
�̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@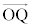 ����ʂ́�
����ʂ́�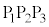 �Ɛ����ł���悢�̂ł����A���ׂĂ݂�ƁA
�Ɛ����ł���悢�̂ł����A���ׂĂ݂�ƁA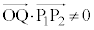 �ƂȂ�A�����������Ƃł��Ȃ��悤�ŁA���������όv�Z���������܂��B
�ƂȂ�A�����������Ƃł��Ȃ��悤�ŁA���������όv�Z���������܂��B
����S�C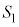 �C
�C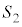 �C
�C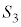 ���A�ǂ�2�̋��ʂ��݂��ɊO��(2�~�̈ʒu�W���Q��)���Ă��邱�Ƃ���A
���A�ǂ�2�̋��ʂ��݂��ɊO��(2�~�̈ʒu�W���Q��)���Ă��邱�Ƃ���A
����S�Ƌ���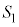 �C
�C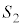 �C
�C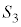 �Ƃ̐ړ_��
�Ƃ̐ړ_��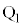 �C
�C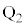 �C
�C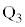 �Ƃ���ƁA
�Ƃ���ƁA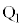 �C
�C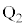 �C
�C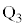 �́A����
�́A����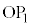 �C
�C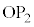 �C
�C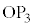 ��̓_�ł����āA����S�̔��a��r�ł��邱�Ƃ���
��̓_�ł����āA����S�̔��a��r�ł��邱�Ƃ���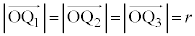 ���(�x�N�g����1���Ɨ����Q��)�A
���(�x�N�g����1���Ɨ����Q��)�A
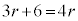 �@��
�@�� 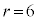 ......[��]
......[��](2) (1)�̌��ʂƇA���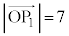 �C
�C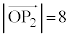 �C
�C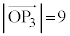 �@����C
�@����C �܂��A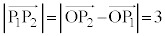 ���(�������Q��)�A
���(�������Q��)�A �� 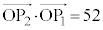 �@����D
�@����D 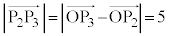 ���A
���A�� 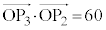 �@����E
�@����E 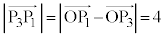 ���A
���A�� 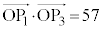 �@����F
�@����F
�l�ʑ̂̒�ʁ�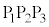 �́A�@���A3�ӂ�3�C4�C5�̐��O�p�`�ŁA��ʐς́A
�́A�@���A3�ӂ�3�C4�C5�̐��O�p�`�ŁA��ʐς́A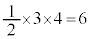 �@����G
�@����G
��ʁ�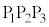 �ɐ����ȃx�N�g�������߂�K�v������܂����A
�ɐ����ȃx�N�g�������߂�K�v������܂����A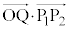 ���v�Z���Ă݂�ƁA
���v�Z���Ă݂�ƁA 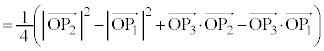
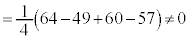 �@(�� �C�C�E�C�F)
�@(�� �C�C�E�C�F)�Ȃ̂ŁA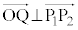 �ł͂���܂���B
�ł͂���܂���B �����ŁA��ʁ�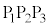 ��̓_H�ŁA
��̓_H�ŁA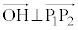 �C
�C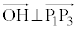 �ƂȂ���̂�T���܂��B
�ƂȂ���̂�T���܂��B �Ƃ����ƁA
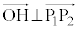 ���A
���A 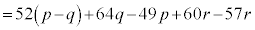 �@(�� �C�C�D�C�E�C�F)
�@(�� �C�C�D�C�E�C�F)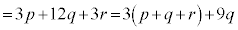 �@(
�@(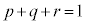 )
)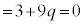 �@��
�@�� 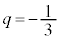 �@����H
�@����H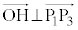 ���A
���A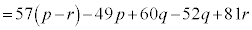 �@(�� �C�C�D�C�E�C�F)
�@(�� �C�C�D�C�E�C�F)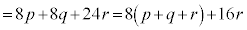 �@(
�@(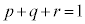 )
)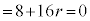 �@��
�@�� 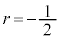 �@����I
�@����I�H�C�I�C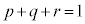 ���A
���A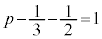 �@��
�@�� 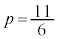 �@����J
�@����J
�H�C�I�C�J���A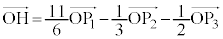
�� 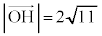 �@����K
�@����K
�G�C�K���A�l�ʑ�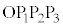 ���̐��́A
���̐��́A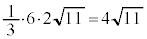 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B