���嗝�H���w'25�N[5]
xy���ʏ�̋Ȑ�C�F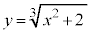 ���l���AC���
���l���AC���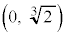 �ȊO�̓_P
�ȊO�̓_P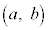 �ɂ�����ڐ���
�ɂ�����ڐ��� �F
�F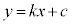 �ƕ\���BC��
�ƕ\���BC�� �̕���������x���������ē�����y�ɂ��Ă�3��������
�̕���������x���������ē�����y�ɂ��Ă�3��������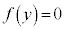 ��b���d���Ƃ��Ă��̂ŁA����1�̉���
��b���d���Ƃ��Ă��̂ŁA����1�̉���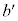 �Ƃ���B�������Ab��3�d���̂Ƃ���
�Ƃ���B�������Ab��3�d���̂Ƃ���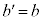 �Ƃ݂Ȃ��B���̖�ɓ�����B
�Ƃ݂Ȃ��B���̖�ɓ�����B
(1) 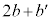 ��k�݂̂̕������ŕ\���B
��k�݂̂̕������ŕ\���B (2) 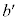 ��b�݂̂̕������ŕ\���B
��b�݂̂̕������ŕ\���B (3) C��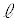 �̋��L�_�ŁA����y���W��
�̋��L�_�ŁA����y���W��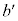 �ł�����̂�
�ł�����̂�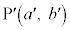 �Ƃ���Ba��b���L�����Ȃ�A
�Ƃ���Ba��b���L�����Ȃ�A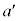 ��
��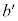 ���L�����ł��邱�Ƃ������B
���L�����ł��邱�Ƃ������B (4) b���p�Cq�ƕ��łȂ�����r��p����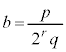 �ŗ^������Ƃ���B�L����
�ŗ^������Ƃ���B�L����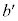 ���
���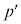 �C
�C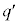 �Ɛ���s��p����
�Ɛ���s��p����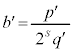 �ƕ\���Ƃ��As��r�̎��ŕ\���B
�ƕ\���Ƃ��As��r�̎��ŕ\���B (5) P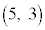 ���Ȑ�C��̓_�ł��邱�Ƃ𗘗p���āAC���x���W��y���W���Ƃ��ɗL�����ł���悤�ȓ_�������ɑ��݂��邱�Ƃ������B
���Ȑ�C��̓_�ł��邱�Ƃ𗘗p���āAC���x���W��y���W���Ƃ��ɗL�����ł���悤�ȓ_�������ɑ��݂��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@������3���������A�ڐ��Ɋւ�����ł��B�U���ɏ���ĉ���悢�̂ł����A�ו��ɒ��ӂ��K�v�Ȗ��ł��B
C�F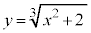
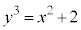 �@����@
�@����@ x����������ƁA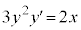 �C
�C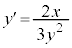
�_P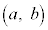 �ɂ�����ڐ��̌X����
�ɂ�����ڐ��̌X����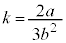 �@����A
�@����A
�_P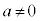 �͋Ȑ�C���
�͋Ȑ�C���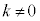 �ȊO�̓_�ł���A
�ȊO�̓_�ł���A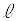 ���
���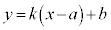 �ł��B
�ł��B
�ڐ�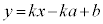 �F
�F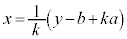 �@����B
�@����B
������@�ɑ������x����������ƁA
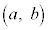
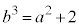 �@����C
�@����C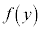 ��C��̓_�ł��邱�Ƃ���@���A
��C��̓_�ł��邱�Ƃ���@���A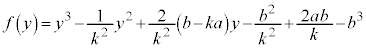 �@����D
�@����D
�C�̍��ӂ�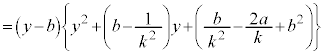 �Ƃ����ƁA�D���A
�Ƃ����ƁA�D���A
�A��p���āA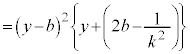 ���A
���A
������3��������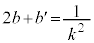 �̉��́A2�d��b�ƁA
�̉��́A2�d��b�ƁA
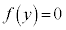 �@����E
�@����E(1) �E���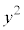 �Ȃ̂ł����A�������ł́A3��������
�Ȃ̂ł����A�������ł́A3��������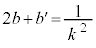 (�C)��
(�C)��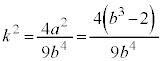 �̌W���ɒ��ڂ��āA���ƌW���̊W���A
�̌W���ɒ��ڂ��āA���ƌW���̊W���A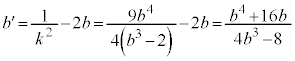 ......[��]
......[��] (2) �A�C�D���A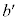
������(1)�̌��ʂ�p���āA
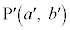 ......[��]
......[��](3) (2)�̌��ʂ��b���L�����Ȃ�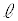 ���L�����ł��B
���L�����ł��B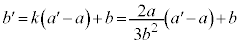 �͐ڐ�
�͐ڐ�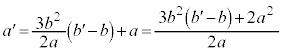 ��̓_�Ȃ̂ŇB�C�A���A
��̓_�Ȃ̂ŇB�C�A���A ������Aa�Cb�C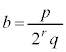 ���L�����Ȃ�
���L�����Ȃ�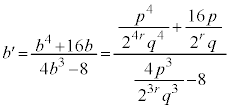 ���L�����ł��B
���L�����ł��B (4) b���p�Cq�ƕ��łȂ�����r��p����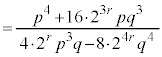 �ŗ^������Ƃ���ƁA(2)�̌��ʂ�p���āA
�ŗ^������Ƃ���ƁA(2)�̌��ʂ�p���āA 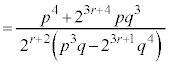 �@(����E���q��
�@(����E���q��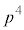 ��������)
��������)�����ŁA���q�́A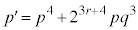 ����A
����A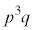 ��
��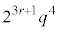 �����R���������ł���A���q��
�����R���������ł���A���q��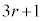 �͊�ł��B����̃J�b�R���́A
�͊�ł��B����̃J�b�R���́A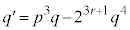 ����A
����A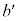 �́A
�́A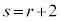 �����R���������ł���A
�����R���������ł���A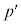 �͊�ł��B
�͊�ł��B
����āA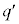 �́A
�́A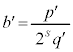 �Ƃ���A�
�Ƃ���A�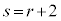 �C
�C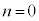 �Ɛ���s��p����
�Ɛ���s��p����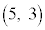 �ƕ\����܂��B
�ƕ\����܂��B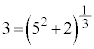 ......[��]
......[��] (5) �Ȑ�C��̓_��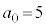 (
(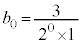 �C
�C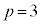 �C
�C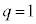 )���l���܂��B
)���l���܂��B 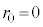 �̂Ƃ��AP
�̂Ƃ��AP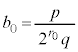 ��
��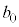 ���Ȑ�C��̓_�ł����āA
���Ȑ�C��̓_�ł����āA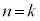 �͗L�����ł���A
�͗L�����ł���A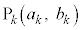 �Ƃ��āA�
�Ƃ��āA�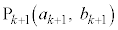 �C
�C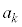 �ƕ��łȂ�����
�ƕ��łȂ�����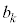 ��p����
��p����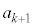 �̌`�ɕ\����܂��B�܂��A
�̌`�ɕ\����܂��B�܂��A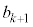 ���L�����ł��B
���L�����ł��B
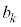 �̂Ƃ��A�Ȑ�C��̓_
�̂Ƃ��A�Ȑ�C��̓_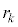 �ɂ�����ڐ��ƋȐ�C�Ƃ̌�_��
�ɂ�����ڐ��ƋȐ�C�Ƃ̌�_��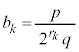 �Ƃ��A
�Ƃ��A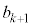 �C
�C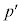 ��L�����ł���Ƃ���A(3)�ɂ��A
��L�����ł���Ƃ���A(3)�ɂ��A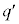 �C
�C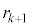 ���L�����ł��B
���L�����ł��B
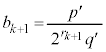 ���p�Cq�ƕ��łȂ�����
���p�Cq�ƕ��łȂ�����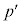 ��p����
��p����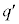 �̌`�ɏ�����Ƃ���ƁA(4)�ɂ��A
�̌`�ɏ�����Ƃ���ƁA(4)�ɂ��A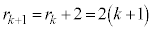 ���
���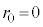 �C
�C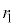 �ƕ��łȂ�����
�ƕ��łȂ�����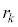 ��p����
��p����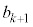 �̌`�ɕ\���܂��B�܂��Ap�Cq�C
�̌`�ɕ\���܂��B�܂��Ap�Cq�C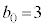 �C
�C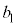 ����ł����āA
����ł����āA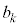 (����
(����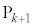 �́A����
�́A����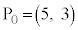 �C����2�̓�������)�́A
�C����2�̓�������)�́A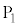 �C
�C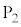 �C���
�C���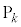 �̑S�ĂƈقȂ�A
�̑S�ĂƈقȂ�A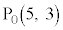 �́A
�́A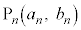 �C
�C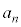 �C����C
�C����C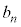 �̑S�ĂƈقȂ�A
�̑S�ĂƈقȂ�A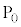 �́A
�́A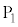 �C
�C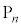 �C
�C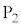 �C����C
�C����C �̑S�ĂƈقȂ�܂��B
�̑S�ĂƈقȂ�܂��B
����āA���w�I�A�[�@�ɂ��A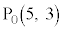 �Cn��0�ȏ�̐����Ƃ��āA�Ȑ�C��̓_
�Cn��0�ȏ�̐����Ƃ��āA�Ȑ�C��̓_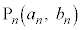 �́A
�́A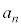 �C
�C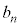 ���L�����ł���A
���L�����ł���A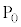 �C
�C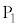 �C����C
�C����C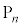 �͑S�ĈقȂ�_�ł��B
�͑S�ĈقȂ�_�ł��B
���R��n�͖����ɑ��݂���̂ŁAC���x���W��y���W���Ƃ��ɗL�����ł���悤�ȓ_�������ɑ��݂��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 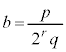 �ŗ^������Ƃ���B�L����
�ŗ^������Ƃ���B�L����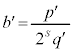 �ƕ\���Ƃ��As��r�̎��ŕ\���B
�ƕ\���Ƃ��As��r�̎��ŕ\���B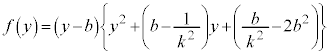
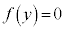
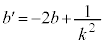
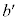
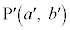 ......[��]
......[��]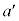
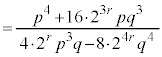 �ŗ^������Ƃ���ƁA(2)�̌��ʂ�p���āA
�ŗ^������Ƃ���ƁA(2)�̌��ʂ�p���āA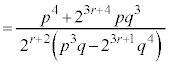 �@(����E���q��
�@(����E���q��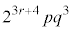
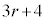
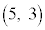 �ƕ\����܂��B
�ƕ\����܂��B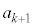 �̌`�ɕ\����܂��B�܂��A
�̌`�ɕ\����܂��B�܂��A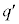 �̌`�ɏ�����Ƃ���ƁA(4)�ɂ��A
�̌`�ɏ�����Ƃ���ƁA(4)�ɂ��A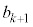 �̌`�ɕ\���܂��B�܂��Ap�Cq�C
�̌`�ɕ\���܂��B�܂��Ap�Cq�C