���嗝�H���w'25�N[1]
���f�����ʏ�ŁA���f��z���~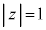 �̏���Ƃ��A
�̏���Ƃ��A
�����_w�̋O�Ղ�C�Ƃ���B���̖�ɓ�����B
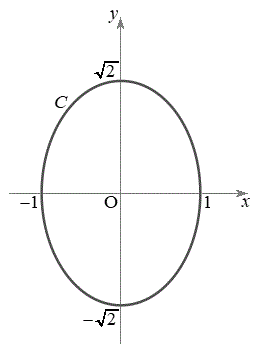
(1) C�͂ǂ̂悤�Ȑ}�`���B���f�����ʏ�ɐ}������B
(2) C�Ɖ~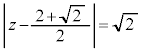 �̋��L�_�����߂�B
�̋��L�_�����߂�B (3) C�ň͂܂��̈��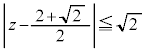 �̕\���̈�̋��ʕ����̖ʐς����߂�B
�̕\���̈�̋��ʕ����̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���f���������Q�Ƃ��Ă��������B�ӊO��2��������������������(2)����ς������肵�܂��B
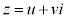 (u�Cv�͎����C
(u�Cv�͎����C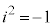 )�Ƃ���ƁA
)�Ƃ���ƁA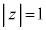 ���A
���A
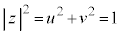 �@����@
�@����@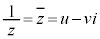 ���A
���A
 (1)
(1) 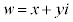 (x�Cy�͎����C
(x�Cy�͎����C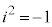 )�Ƃ���ƁA�A���A
)�Ƃ���ƁA�A���A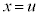 �C
�C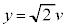
�@���A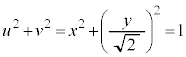 �@����B
�@����B
����āAC���ȉ~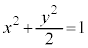 �Ő}������ƉE�}�B
�Ő}������ƉE�}�B (2) 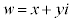 (x�Cy�͎����C
(x�Cy�͎����C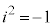 )�Ƃ���ƁA�~
)�Ƃ���ƁA�~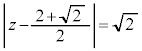 �́A
�́A 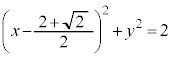 �@����C
�@����C�ł��B�B�C�C��A������ƁA
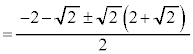 �@����D
�@����D���L�_�͇C��Ɉʒu����̂ŁA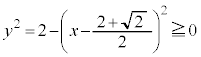 ���A
���A ���D���W���ʏ�ł�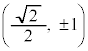 �ł��B
�ł��B 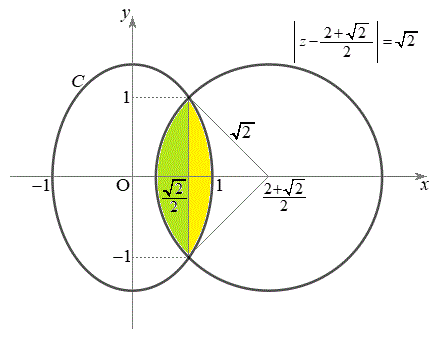 (3) C�ň͂܂��̈��
(3) C�ň͂܂��̈��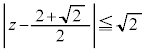 �̕\���̈�̋��ʕ����́A�E�}���F���F���Ɖ��ΐF���F�������킹�������ł��B
�̕\���̈�̋��ʕ����́A�E�}���F���F���Ɖ��ΐF���F�������킹�������ł��B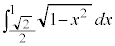 �́A���a1�̉~�̖ʐς�
�́A���a1�̉~�̖ʐς�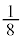 ����1��1�̐����`�̖ʐς�
����1��1�̐����`�̖ʐς�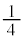 ���������ʐςɓ�����(�u���ϕ�(����2)���Q��)�A
���������ʐςɓ�����(�u���ϕ�(����2)���Q��)�A����āA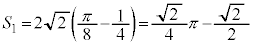
�E�}���ΐF���F���̖ʐ�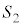 �́A���a
�́A���a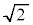 �̉~�̖ʐς�
�̉~�̖ʐς�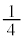 ����1��
����1��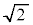 �̐����`�̖ʐς�
�̐����`�̖ʐς�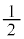 ���������ʐςɓ�����
���������ʐςɓ����� ���߂�ʐς́A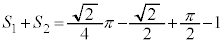 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 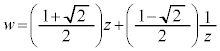
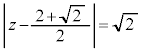 �̋��L�_�����߂�B
�̋��L�_�����߂�B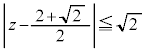 �̕\���̈�̋��ʕ����̖ʐς����߂�B
�̕\���̈�̋��ʕ����̖ʐς����߂�B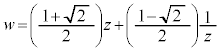
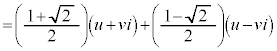
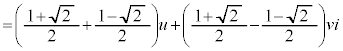
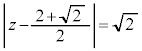 �́A
�́A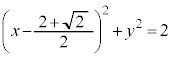 �@����C
�@����C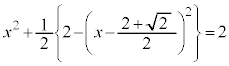
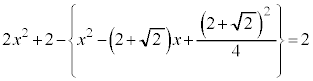
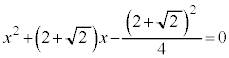
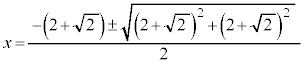
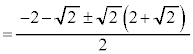 �@����D
�@����D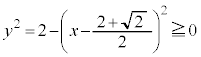 ���A
���A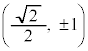 �ł��B
�ł��B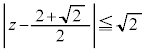 �̕\���̈�̋��ʕ����́A�E�}���F���F���Ɖ��ΐF���F�������킹�������ł��B
�̕\���̈�̋��ʕ����́A�E�}���F���F���Ɖ��ΐF���F�������킹�������ł��B