���嗝�H���w '25 �N [3] 1 ���� n �܂ł̈قȂ鎩�R���� 1 �������ꂽ n ���̃J�[�h�����ɕ���ł���B���̂Ƃ��A�ǂ̃J�[�h�����݂Ƃ͈قȂ�ʒu�Ɉړ�����悤�ɕ��בւ��Ăł��鏇��̑����� (1) �̒l�����߂�B (2) �̂Ƃ��A (3) �̂Ƃ��A n ��p���ĕ\���B �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �@������� ���ʃe�X�g���w IA22 �N�� 3 �� ���v���o���܂����A�����������ɓ���Ȃ��Ă��܂��B (1) 1 ���� 4 �܂ł̎��R���������ꂽ�J�[�h�̕��ו��� ( ���� ���Q�� ) �B 4 ��ނ̃J�[�h�̂��� 1 �������ʒu���ς��Ȃ����ו��́A�ς��Ȃ� 1 ���̑I�ѕ��� 4 �ʂ�A 3 �����قȂ�ʒu�Ɉړ�����̂� 4 ��ނ̃J�[�h�̂��� 2 �������ʒu���ς��Ȃ����ו��́A 2 ���̑I�ѕ��� 2 �����قȂ�ʒu�Ɉړ�����̂� 4 ���̃J�[�h���ׂĈʒu���ς��Ȃ��̂� 1 �ʂ�B����āA ......[ �� ] �ʉ��D 1 ���� 4 �܂ł̎��R���������ꂽ�J�[�h�� 2 �ʂ�ɕ����܂��B (i) ���݈ʒu�� (3 �ʂ� ) �� 2 ���̈ʒu�����ւ��܂��B 2 ���� 2 �����قȂ�ʒu�Ɉړ�������̂� (ii) �C ( �ʂ� ) ��ɁA ( ���� ) �� (i) �� (ii) �ɂ͏d�����Ȃ��A�܂� (i) �� (ii) �ŁA�ǂ̃J�[�h�����݂Ƃ͈قȂ�ʒu�Ɉړ�����悤�ɕ��בւ��邷�ׂĂ̏ꍇ�ɂȂ�܂��B����āA (2) ��L�̕ʉ��̕��@�ōl���܂��B 1 ���� n �܂ł̎��R���������ꂽ�J�[�h�� (i) ���݈ʒu�� ( �ʂ� ) �� 2 ���̈ʒu�����ւ��܂��B�c�� (ii) �C ( �������� ( �ʂ� ) ��� ( ���� ) �� (i) �� (ii) �ɂ͏d�����Ȃ��A�܂� (i) �� (ii) �ŁA�ǂ̃J�[�h�����݂Ƃ͈قȂ�ʒu�Ɉړ�����悤�ɕ��בւ��邷�ׂĂ̏ꍇ�ɂȂ�܂��B����āA ......[ �� ] (3) (2) �̌��ʂ�p���āA �@����@ �@����A �@�C�A������ׂāA
����āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���嗝�H���w TOP �@�@ ���w TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� �Ȃ��A�́A © 2005-2025 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� �� 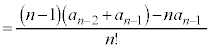
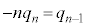 �@����A
�@����A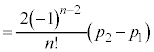
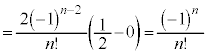
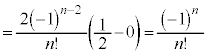 ......[��]
......[��]