���K'08�N[17]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
(2���ԑQ����) 2�_A�CB�ƁA���̏��1�̐�����B���̐́A����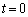 �ł͓_A�ɂ���A���̌�A���̋K��(a)�C(b)�ɂ��������ē����B
�ł͓_A�ɂ���A���̌�A���̋K��(a)�C(b)�ɂ��������ē����B
�e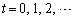 �ɑ��āA
�ɑ��āA
(a) ����t�ɐ��_A�ɂ���A����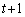 �ɐ��_A�ɂ���m����c�C�_B�ɂ���m����
�ɐ��_A�ɂ���m����c�C�_B�ɂ���m����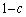 �ł���B
�ł���B (b) ����t�ɐ��_B�ɂ���A����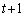 �ɐ��_B�ɂ���m����2c�C�_A�ɂ���m����
�ɐ��_B�ɂ���m����2c�C�_A�ɂ���m����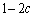 �ł���B
�ł���B �������Ac��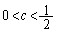 �����萔�Ƃ���B
�����萔�Ƃ���B
���܁An�����R���Ƃ��A����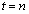 �ɂ����Đ��_A�ɂ���m����
�ɂ����Đ��_A�ɂ���m����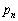 �Ƃ���Ƃ��A���̖₢�ɓ�����B
�Ƃ���Ƃ��A���̖₢�ɓ�����B
(1) 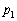 �C
�C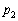 �����߂�B
�����߂�B (2) 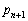 ��
��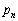 ��c��p���ĕ\���B
��c��p���ĕ\���B (3) 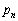 �����߂�B
�����߂�B (4) 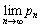 �����߂�B
�����߂�B (�L���嗝�n'08�O��)
���@(1) 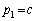 ......[��]
......[��] A��B��A�ƂȂ��m����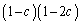 A��A��A�ƂȂ�m����
A��A��A�ƂȂ�m����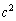
�� 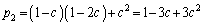 ......[��]
......[��]
(2) ����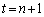 ��A�ɂ���(�m��
��A�ɂ���(�m��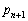 )�̂́A����
)�̂́A����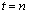 ��A�ɂ���(�m��
��A�ɂ���(�m��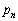 )�A�m��c��A�Ɏc�邩�A�܂��́A����
)�A�m��c��A�Ɏc�邩�A�܂��́A����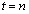 ��B�ɂ���(�m��
��B�ɂ���(�m��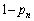 )�A�m��
)�A�m��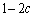 ��A�Ɉڂ�ꍇ������A
��A�Ɉڂ�ꍇ������A
(3) �@��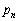 ��
��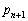 ��α�ɒu��������ƁA
��α�ɒu��������ƁA 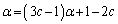 �@����A
�@����A�� 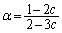 �@(
�@(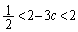 )�@�|�A�����ƁA
)�@�|�A�����ƁA
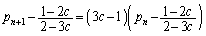
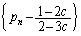 �́A����
�́A����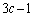 �����䐔���B�����́A
�����䐔���B�����́A �� 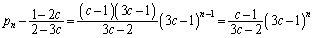 ��
�� 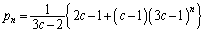 ......[��]
......[��]
(4) 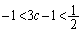 ���A
���A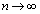 �̂Ƃ��A
�̂Ƃ��A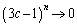 �@(�Ɍ����Q��)
�@(�Ɍ����Q��) ����āA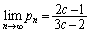 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B