���ϔ���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���n(�Ȃ���������)�ɂ����āA���σx�N�g��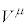 ��
��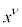 �Ŕ������邱�Ƃ��l���܂��Bx������ψ�
�Ŕ������邱�Ƃ��l���܂��Bx������ψ�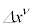 ������
������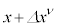 �C���҂ł�
�C���҂ł�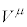 �̍����Ƃ���
�̍����Ƃ���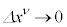 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A
�Ƃł���Ηǂ��̂ł����A��ʍ��W�n�ł́A�قȂ鐢�E�_x��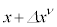 �̊Ԃł́A������W�n�̘c�݂̉e�����Ă��܂����߁A�x�N�g���̍�����邱�Ƃ��ł��Ȃ��̂ł��B���Ȃ݂ɁA���[�����c�ϊ��ɂ��
�̊Ԃł́A������W�n�̘c�݂̉e�����Ă��܂����߁A�x�N�g���̍�����邱�Ƃ��ł��Ȃ��̂ł��B���Ȃ݂ɁA���[�����c�ϊ��ɂ��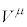 ��
��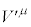 �ƕϊ������Ƃ��A
�ƕϊ������Ƃ��A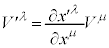 �ƕ\���܂��B�����
�ƕ\���܂��B�����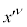 �őf���ɔ�������ƁA�A���藝�F
�őf���ɔ�������ƁA�A���藝�F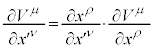 ���A
���A
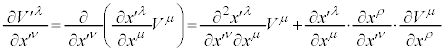 �@����@
�@����@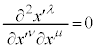 �ł���A��2�����������c���āA
�ł���A��2�����������c���āA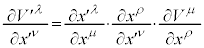 �ƂȂ�A
�ƂȂ�A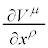 �������e���\���Ƃ��ĕϊ�����܂��B���R�Ȏ���ɂ����郍�[�����c�ϊ��ł́A
�������e���\���Ƃ��ĕϊ�����܂��B���R�Ȏ���ɂ����郍�[�����c�ϊ��ł́A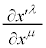 ���萔�ƂȂ�̂ŁA
���萔�ƂȂ�̂ŁA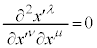 �ƂȂ�A
�ƂȂ�A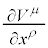 �͍����e���\���̂悤�ɐU�镑���܂��B�ł����A���E�_���Ƃ�
�͍����e���\���̂悤�ɐU�镑���܂��B�ł����A���E�_���Ƃ�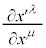 ���قȂ�悤�ȕϊ��ł́A
���قȂ�悤�ȕϊ��ł́A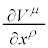 �������e���\���ɂȂ�Ȃ��̂Œ��ӂ��K�v�ł��B
�������e���\���ɂȂ�Ȃ��̂Œ��ӂ��K�v�ł��B
�����ŁA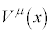 �𐢊E�_
�𐢊E�_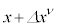 �̈ʒu�܂ŕ��s�ړ�������
�̈ʒu�܂ŕ��s�ړ�������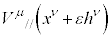 ��
��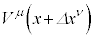 �̍������A
�̍������A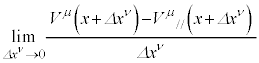 ���l���܂��B
���l���܂��B
�Ƃ����ƁA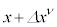 �ߖT�ŋǏ��I�ɕ��R���Ƃ���A
�ߖT�ŋǏ��I�ɕ��R���Ƃ���A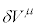 ��
��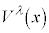 ��
��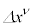 �ɔ�Ⴗ��ƍl�����A���萔��
�ɔ�Ⴗ��ƍl�����A���萔��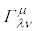 �Ƃ����ƁA
�Ƃ����ƁA
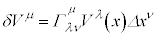 �@����A
�@����A
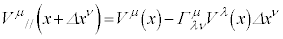 �@����B
�@����B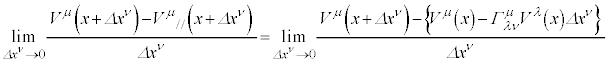
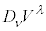 �Ə������Ƃɂ��܂�(��发�ł͕ʂ̏����������Ă��邱�Ƃ�����܂�)�B�c��ԏ�ł͔����͋��ϔ����ōl���܂��B�܂�A
�Ə������Ƃɂ��܂�(��发�ł͕ʂ̏����������Ă��邱�Ƃ�����܂�)�B�c��ԏ�ł͔����͋��ϔ����ōl���܂��B�܂�A
���σx�N�g���̋��ϔ����F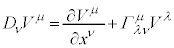 �@����C
�@����C 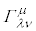 ���N���X�g�b�t�F���̋L���ƌ����܂��B����̊w�I��\���܂��B�e���\���̂悤�Ɍ����܂����e���\���ł͂���܂���B
���N���X�g�b�t�F���̋L���ƌ����܂��B����̊w�I��\���܂��B�e���\���̂悤�Ɍ����܂����e���\���ł͂���܂���B
���ɁA���σx�N�g���̔������l���܂��B�܂��A�C�ӂ̔��σx�N�g��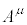 �Ƌ��σx�N�g��
�Ƌ��σx�N�g��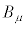 �̃X�J���[��
�̃X�J���[��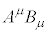 �́A���s�ړ��ł͕ω����Ȃ��̂ŁA
�́A���s�ړ��ł͕ω����Ȃ��̂ŁA
�A���A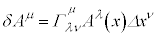 �Ȃ̂ŁA
�Ȃ̂ŁA
�E�ӂ̓Y����λ��μ�͏k�Ă���̂ŁA����ւ��Ă��l�ɕω��͂���܂���B����āA
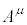 �͔C�ӂ̔��σx�N�g���Ȃ̂ŁA
�͔C�ӂ̔��σx�N�g���Ȃ̂ŁA
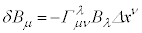 �@����D
�@����D
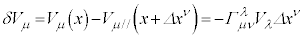 �@��
�@�� 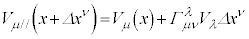
�܂�A���σx�N�g���̋��ϔ����F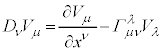 �@����E
�@����E
�ƂȂ�܂��B
2�̔��σx�N�g��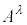 �C
�C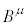 �̐�
�̐�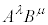 �ɂ��āA�A���A
�ɂ��āA�A���A
�C�̓��o�Ɠ��l�ɂ��āA
������A���σe���\��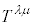 �̋��ϔ����́A
�̋��ϔ����́A
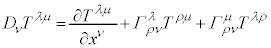 �@����F
�@����F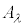 �C
�C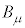 �̐�
�̐�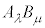 �ɂ��āA�D���A
�ɂ��āA�D���A
�E�̓��o�Ɠ��l�ɂ��āA
������A���σe���\��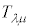 �̋��ϔ����́A
�̋��ϔ����́A
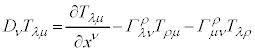 �@����G
�@����G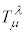 �̋��ϔ����́A
�̋��ϔ����́A
�ƂȂ�܂��B
�E�ŁA�Y����ν��μ�����ւ������Ƃō����Ƃ�ƁA
�����ŁAϕ���X�J���[���Ƃ��āA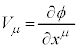 �̏ꍇ���l���܂��B
�̏ꍇ���l���܂��B
���ϔ����̓e���\���Ȃ̂ŁA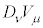 �̓e���\���ł��̍����e���\���ł���A�K�����C�n�ɂ����Ă͒ʏ�̔����Ɉ�v���č��ӂ�0�ƂȂ�A������W�n�Ń[���ɂȂ�A���̍��W�n�ł��[���ɂȂ�܂��B�܂�A
�̓e���\���ł��̍����e���\���ł���A�K�����C�n�ɂ����Ă͒ʏ�̔����Ɉ�v���č��ӂ�0�ƂȂ�A������W�n�Ń[���ɂȂ�A���̍��W�n�ł��[���ɂȂ�܂��B�܂�A
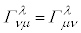 �@����H
�@����H
�����ŁA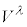 ��C�ӂ̔��σx�N�g���Ƃ��āA��̕��s�ړ��ɂ����ăx�N�g����4���I����
��C�ӂ̔��σx�N�g���Ƃ��āA��̕��s�ړ��ɂ����ăx�N�g����4���I����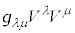 ���s�ςł���A�Ƃ�������������܂��B���E�_x�ɂ�����v�ʃe���\����
���s�ςł���A�Ƃ�������������܂��B���E�_x�ɂ�����v�ʃe���\����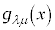 �C�x�N�g����
�C�x�N�g����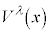 �C���E�_
�C���E�_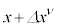 �ɂ�����v�ʃe���\����
�ɂ�����v�ʃe���\����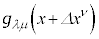 �C
�C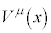 �s�ړ������x�N�g����
�s�ړ������x�N�g����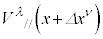 �Ƃ��āA
�Ƃ��āA
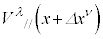 �C
�C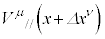 �ɁA�B��������ƁA
�ɁA�B��������ƁA
����ɁA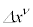 ������ʂł���Ƃ��āA
������ʂł���Ƃ��āA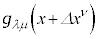 ��
��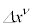 �œW�J����ƁA
�œW�J����ƁA
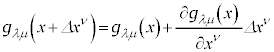 �@(
�@(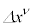 ��2��ȏ��)
��2��ȏ��)
�E�ӂ�W�J���A�����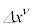 ��2��ȏ������ƁA
��2��ȏ������ƁA
���J�b�R���ɂ��āA�Y����t���ւ��邱�Ƃɂ��A
����������A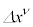 �Ŋ���ƁA
�Ŋ���ƁA
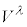 ��C�ӂ̔��σx�N�g���Ƃ����̂ŁA
��C�ӂ̔��σx�N�g���Ƃ����̂ŁA
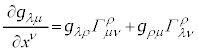 �@����I
�@����I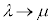 �C
�C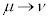 �C
�C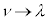 �Ɠ���ւ��āA
�Ɠ���ւ��āA
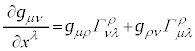 �@����J
�@����J
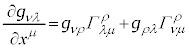 �@����K
�@����K
���ӂ�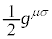 ��������ƁA
��������ƁA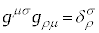 �C
�C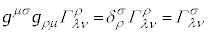 ���A
���A
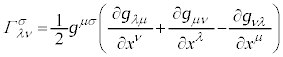 �@����L
�@����L
�C��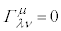 �C�܂��A�E��
�C�܂��A�E��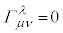 �Ƃł���A���ϔ����͒ʏ�̔����ɂȂ�܂��B�����ŇL�ɂ��A�N���X�g�b�t�F���̋L�����Ǐ��I��0�ɂł���悤�ȋǏ������n���l���邱�ƂɂȂ�܂��B
�Ƃł���A���ϔ����͒ʏ�̔����ɂȂ�܂��B�����ŇL�ɂ��A�N���X�g�b�t�F���̋L�����Ǐ��I��0�ɂł���悤�ȋǏ������n���l���邱�ƂɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 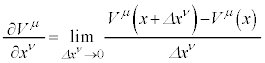
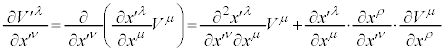 �@����@
�@����@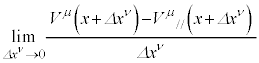 ���l���܂��B
���l���܂��B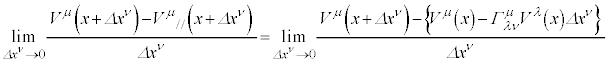
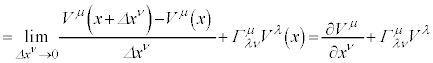
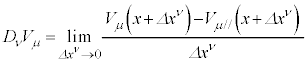
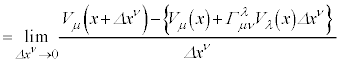
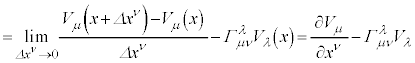
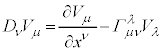 �@����E
�@����E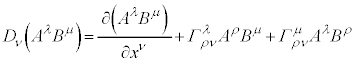
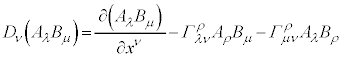
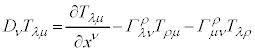 �@����G
�@����G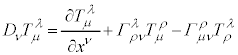
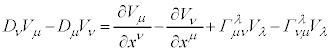
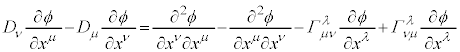
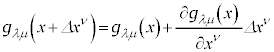 �@(
�@(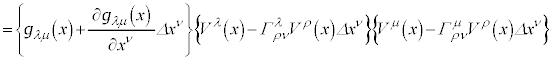
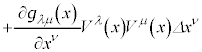
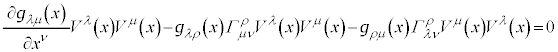
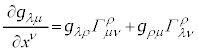 �@����I
�@����I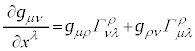 �@����J
�@����J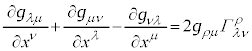
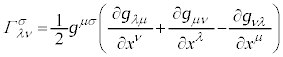 �@����L
�@����L